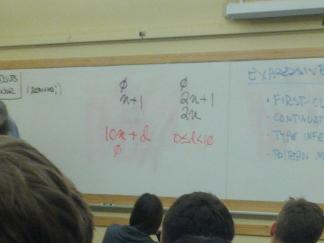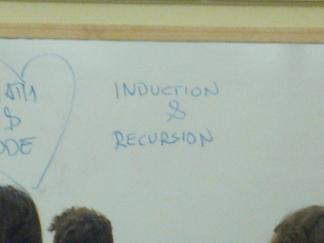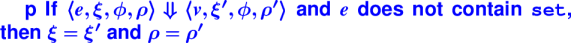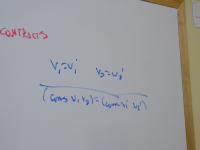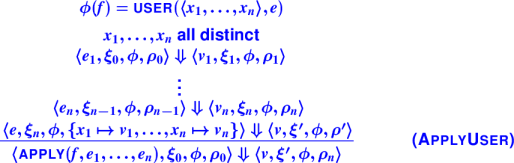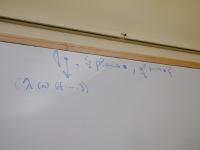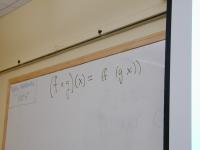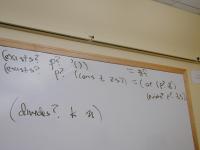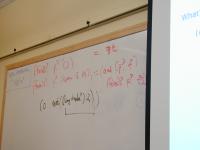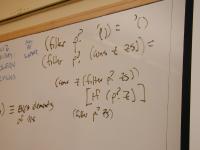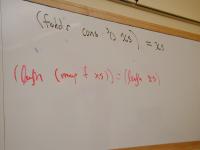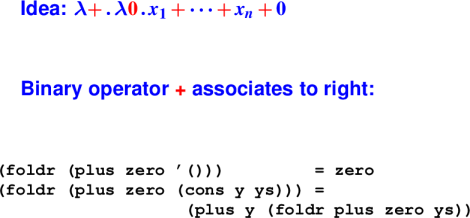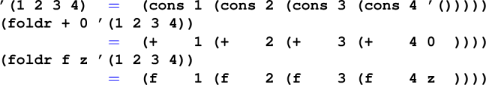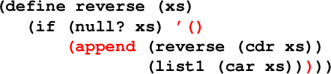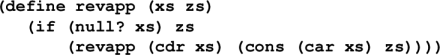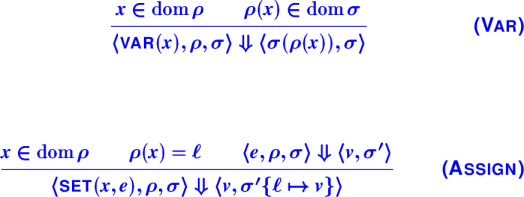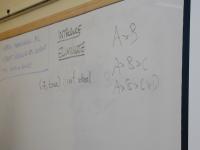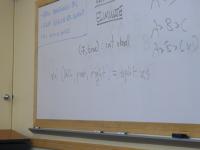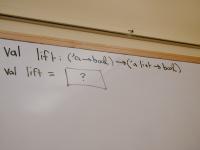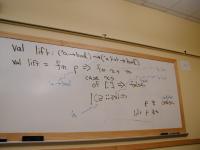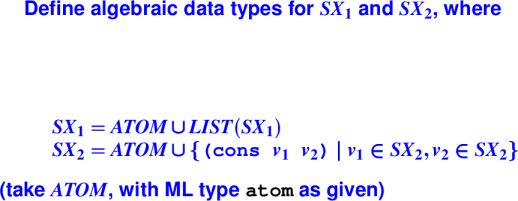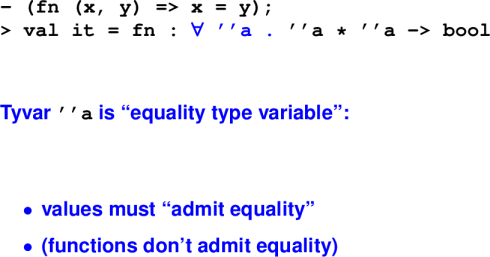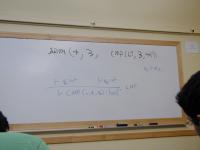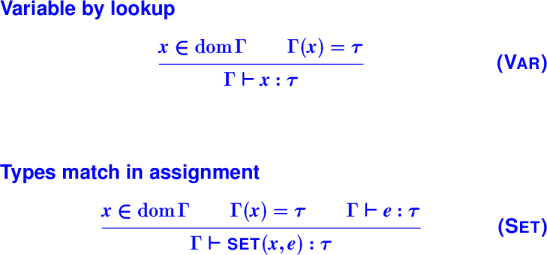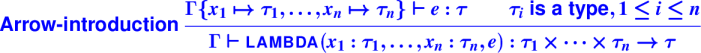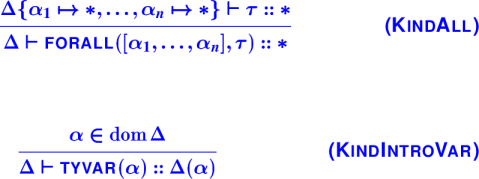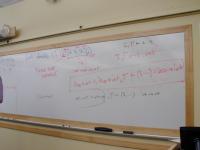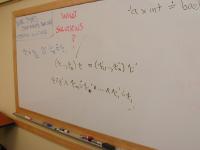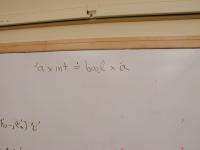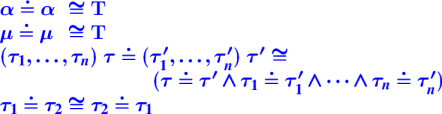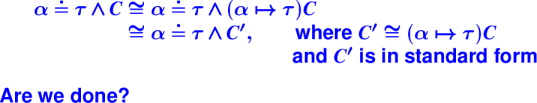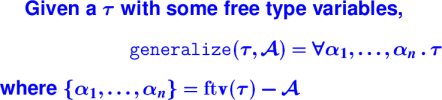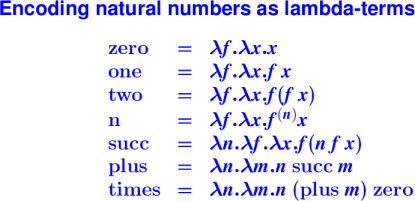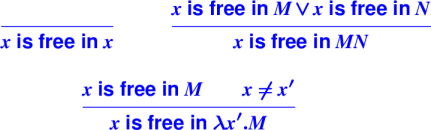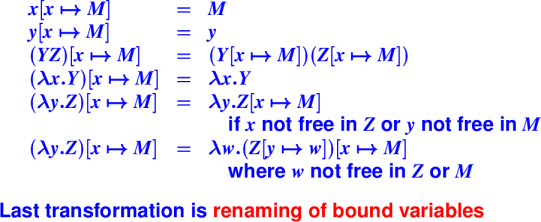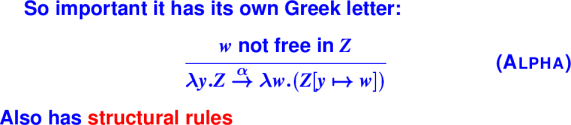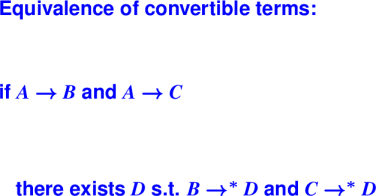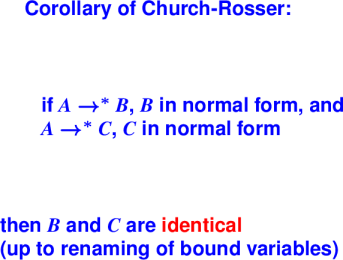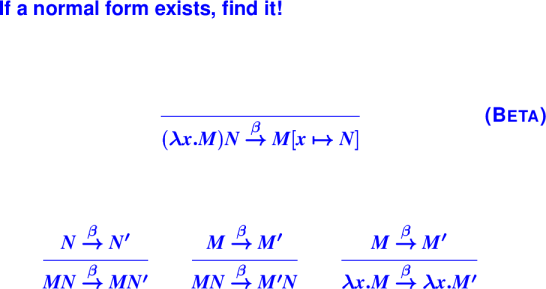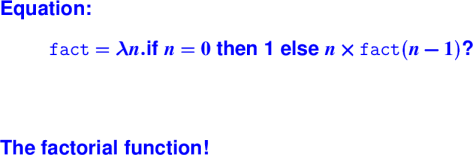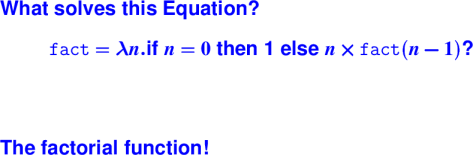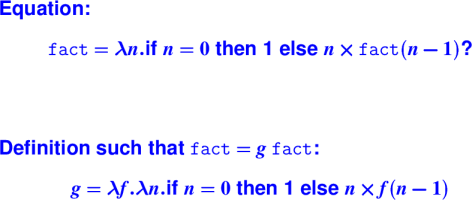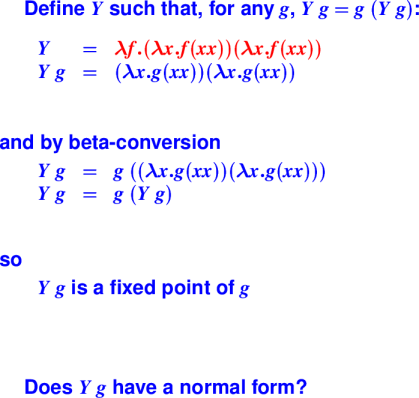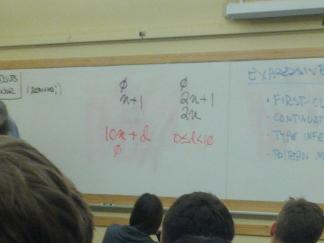








- Java in January
- Forth in February
- Matlab in March
- Ada in April
What if the course were called "Houses"?
The same thing for programming languages:
- The marriage of math and code
- Induction and recursion
If you're going to enjoy the course,
- You should enjoy programming (15)
- You should also like math (61, sort of---induction and proofs)
- You should be willing to work hard
Topic of study: the stuff software is made of
- Thousands
- Each one unique
- Why do you suppose so many?
Conclusion: make it easier to write programs that really work
- An invaluable skill for all you software practitioners
In public: a language should express computations
- Precisely
- At a high level
- In a way we can reason about
So, no more uncivilized low-level C, and no more C++ that no mortal being can understand
In the pub: professionals are keenly interested in their code
Your language can make you or break you.
New ways of thinking about programming
Become a sophisticated consumer, aware of old wine in new bottles
Double your productivity
Bonus: preparation for advanced study (This course serves two audiences)
- Course has to serve everyone from fresh out of 15/61 to grad students
Intellectual tools you need to understand, evaluate, and use languages effectively
Notations of the trade (source of precision, further study)
Learn by doing:
- Lots of short programs
- High power-to-weight ratio (lots of thought per line)
Just as intellectually challenging as COMP 40, but in an entirely different direction.
Language shapes your thinking
There aren't that many great features, and you will see them over and over
You'll choose features, and therefore languages, to fit your needs
Some are more powerful than others
In Comp 105,
Only the most powerful features need apply
We explode your brain so you can think differently
You'll know you're doing it right if at first your head hurts terribly, then you have a breakthrough moment and it all seems pleasant afterwards
To say more with less (expressive power):
- First-class functions
- Continuations
- Type inference
- Pattern matching
To promote reliability and reuse:
- Type polymorphism
- Abstract data types
- Modules and "generics"
- Objects and inheritance
Describing it all precisely:
- Operational semantics (daily tool of the trade)
- Denotational semantics (sheer beauty of the ideas, source of much code)
Three lectures per week: 50% more cracks at tough ideas
Schedule is still a work in progress:
- Last year I made a huge mistake: 30/60/60 instead of 50/50/50
You must get my book
Homework will be frequent and challenging:
- Many small programming problems
- Some theory problems, more like a math problem set
- The occasional larger project, like a type checker or a game solver
- Submit electronically
- Theory is easier to do by hand; scan it and submit PDF
Both individual and pair work:
- All problems should be discussed with others
(Essential to your success)
- Discussions must be acknowleged
- Most problems must be completed individually
- Do not allow anyone else to see your code
For some problems larger in scope, you will work in pairs
Be very careful to separate your pair work and your individual work. (A mistake could be major violation of academic integrity, with severe penalties.)
Questions and answers on Piazza
You don't just ask questions; you also get credit for answering them
Course staff has apps for their phones
Be super careful that any question containing your code must be private. (This is an issue of academic integrity.)
Other policies and procedures in handout and on web
Ways a recursive function could decompose a natural number n.
Peel back one:
n = 0
n = m + 1, m is also a natural number
Split into two pieces:
n = 0
n = k + (n - k) 0 < k < n (everything gets smaller)
Sequence of decimal digits (see study problems on digits)
n = d, where 0 <= d < 10
n = 10 * m + d, where 0 <= d < 10 and m > 0
To do your homework problems, which I recommend starting today, you'll need to invent at least one more.
(Why start early? To put your back brain to work.)
Call me "Norman," "Professor Ramsey", or "Mister Ramsey." In a pinch, "Professor" will do.
Cultural enrichment: Paul Graham, especially the "Blub paradox"
I am also trying to solve two of the most important problems identified by your predecessors:
Students want more time between the last lecture on a topic and the deadline for the homework
Students want feedback on homework quickly, in time for the next assignment.
We are working toward this.
For this reason, the first homework is tiny: I broke off a tiny piece and called it a homework assignment. It's there to get you moving quickly. Everything you need to think about is in Wednesday's discussion of recursive functions that consume natural numbers.
Looks something like this:
| impcore |
one star |
| opsem |
two stars |
| scheme |
three stars |
| hofs |
four stars |
And it's more or less four-star homeworks from there on out.
Lesson: don't make decisions based on the first couple of homeworks!
Many will be announced in advance. Some will not. My goal in having quizzes is that you come to lecture prepared to engage more deeply with the ideas, techniques, and notations. For that reason I am counting quiz grades toward class participation.
Quizzes will start when I feel well enough to write some. Perhaps next week or the week after.
You'll see:
We don't cover everything in lecture
Lecture is for just the hard parts
We'll talk very little about the code (just the interesting bits)
In a 100-level course, you are responsible for your own learning
Course evaluations: a few students want everything gone over in lecture. That's not how things work in real life, and that's not how things work here. We point you in the right direction and identify traps and pitfalls, and we find good problems for you to work on.
If you're expecting to see everything in lecture, you have a couple of choices: change your expectations, or take the course next year when you will have more experience and will be ready to take charge of your own stuff.
Last time: refresher on recursion. Go for homework!
This week: abstract syntax and operational semantics (next homework)
Programming-languages people are wild about compositionality.
- Build sensible things from sensible pieces using just a few construction principles.
Example of compositionality: syntax (grammar)
Programming languages more orderly than natural language.
Example of non-compositionality
Open question: what are all the representations of a while loop?
(Answers on board)
Our common framework
Goal: eliminate superficial differences
- Makes comparisons easy
- Differences that remain must be important!
No new language ideas.
Imperative programming with an IMPerative CORE:
Idea of LISP syntax
Parenthesized prefix syntax:
Examples:
(+ 2 2)
(if (isbound? x rho) (lookup rho x) (error 99))
Syntactic structure of Impcore
Two syntactic categories: definitions, expressions (no statements!)
An Impcore program is a sequence of definitions
(define mod (m n) (- m (* n (/ m n))))
Compare
int mod (int m, int n) {
return m - n * (m / n);
}
Impcore variable definition
Example
(val n 99)
Compare
int n = 99;
Also, expressions at top level (definition of it)
Impcore expressions
No statements means expression-oriented:
(if e1 e2 e3)
(while e1 e2)
(set x e)
(begin e1 ... en)
(f e1 ... en)
Each one has a value and may have side effects!
Functions are primitive (+ - * / = < > print)
or defined with (define f ...).
The only type of data is "machine integer" (deliberate oversimplification)
Scopes also called "name spaces"; we will call them "environments" because that's the pointy-headed theory term---and if you want to read some of the exciting papers, pointy-headed theory has to be second nature.
Names known in "environments"
Ways to talk about meanings of names:
- Scope rules
- Name spaces
- Environments (aka symbol tables)
Impcore vars in 2 environments: globals, formals
There are no local variables
- Just like awk; if you need temps, use extra formal parameters
- For homework, you'll add local variables
Functions live in their own environment (not shared with variables)
Environmental abuse
Abuse of separate name spaces:
-> (val f 33)
33
-> (define f (x) (+ x x))
f
-> (f f)
66
Concrete syntax for Impcore
Definitions and expressions:
def ::= (val x exp)
| exp
| (define f (formals) e)
| (use filename)
exp ::= integer-literal
| variable-name
| (set x exp)
| (if exp1 exp2 exp3)
| (while exp1 exp2)
| (begin exp1 ... expn)
| (op exp1 ... expn)
op ::= function-name | primitive-name
Abstract syntax
Exp = LITERAL (Value)
| VAR (Name)
| SET (Name name, Exp exp)
| IFX (Exp cond, Exp true, Exp false)
| WHILEX (Exp cond, Exp exp)
| BEGIN (Explist)
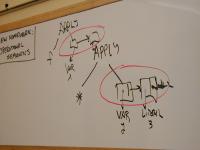
| APPLY (Name name, Explist actuals)
One kind of "application" for both user-defined and primitive functions.
Representing abstract syntax
typedef struct Exp *Exp;
typedef enum {
LITERAL, VAR, SET, IFX, WHILEX, BEGIN, APPLY
} Expalt; /* which alternative is it? */
struct Exp { // only two fields: 'alt' and 'u'!
Expalt alt;
union {
Value literal;
Name var;
struct { Name name; Exp exp; } set;
struct { Exp cond; Exp true; Exp false; } ifx;
struct { Exp cond; Exp exp; } whilex;
Explist begin;
struct { Name name; Explist actuals; } apply;
} u;
};
Example AST for (f x (* y 3)) (using Explist)
Example Ast for (define abs (x) (if (< x 0) (- 0 x) x)) (using Namelist)
Trick question:
What's the value of (* y 3)? OK, what's its meaning?

Tonight's homework
Piazza:
- If you're active on Piazza, please put up a photo. It will help me learn your names.
Next homework:
Greek letters on the web server are broken
PDF on the web server might be OK
Homework was finalized at the very last minute. If anything is unclear, ask, and if there are changes, I will announce on Piazza.
The only likely changes are to the section on how your work will be evaluated.
Waiting list:
- If you have been "purged," get an add/drop form. I'll sign it.
Bare possibility of an office our from me this afternoon.
With my help, Geoff Mainland put together some terrifying Beamer slides

I owe you an apology. Inductive structure was way harder than I realized. I broke a cardinal rule (always do all the problems before they are assigned).
Let's look at just one:
(binary 5) == 101
(binary 3) == 11
What's the inductive structure of the input?
OK, moving on to contracts!
*Structure of the input drives the structure of the code.
To discover recursive functions, write algebraic laws:
exp x 0 = 1
exp x (n + 1) = x * (exp x n)
Can you find a direction in which something gets smaller?
Another example:
binary 0 = 0
binary (2n + b) = binary n .. b
Right-hand sides in arithmetic?
binary (2n + b) = 10 * binary n + b
Which direction gets smaller? What's the code?
Programming with assignments etc
Recursion and composition:
Recursive function boot camp
Two recursive data structures: the list and the S-expression
More powerful ways of putting functions together (compositionality again, and it leads to reuse)
As a lens for understanding, you can ask these questions about any language:
What is the abstract syntax? What are the syntactic categories, and what are the terms in each category?
What are the values? What do expressions/terms evaluate to?
What environments are there? That is, what can names stand for?
How are terms evaluated? What are the judgments? (What are the rules?)
What's in the initial basis? Primitives and otherwise, what is built in?
Question 2: what are the values?
Two new kinds of data:
Pointer to automatically managed cons cell (mother of civilization)
The function closure: not just a datum, a feature
(The setting is Scheme)
Values are S-expressions.
Comforting lies:
An S-expression is a symbol or a literal integer or a literal Boolean or a list of S-expressions.
A list of S-expressions is either - the empty list '() - an S-expression followed by a list of S-expressions
Like any other abstract data type
creators create new values of the type
producers make new values from existing values
observers examine values of the type
mutators change values of the type
N.B. creators + producers = constructors
No mutators in uScheme
S-expression observers
number?
symbol?
boolean?
null?
Creators and producers: nil and cons
'()
(cons S' S)
More examples:
(cons 'a '())
(cons 'a '(b))
Note the literal '(b). (Not covered in class.)
Inductive definition of lists:

Observers: car, cdr, null?, pair? (also known as "first" and "rest", "head" and "tail", and many other names)
Algebraic laws of lists:
(null? '()) == #t
(null? (cons v vs)) == #f
(car (cons v vs)) == v
(cdr (cons v vs)) == vs
Combine creators/producers with observers
Inductively defined data type: smallest set satisfying this equation:
Inductive definition of lists:

Any list is therefore constructed with nil or with cons.
- How can you tell the difference?
- What, therefore, is the structure of a function that consumes a list?
Example: length







Today's homework:
How you're doing on each dimension: just tell us exemplary, satisfactory, or needs improvement. If your work falls short of exemplary, and if you feel like it, you can tell us in a few words where you believe you fell short.
Summary: we're looking for your self-evaluation, not for evidence
Where Monday's proof breaks down: in the APPLY-USER rule, the induction hypothesis says that if the expression has no SET, then ξ does not change. If the application has no SET, then none of the actual parameters has SET. But the function body may have SET, so the induction hypothesis cannot guarantee that ξ is unchanged.
In other words, even if your own code has no SET, if you call a function that has SET, it might change a global variable.
Scheme homework advice:
Unlike operational semantics, don't wait for lecture
Get out ahead and then you'll know what problems lecture might solve for you
What's next
More truth about S-expressions
More practice writing recursive functions
Maybe start to look at costs
The truth about S-expressions:

Polymorphic means "operating on values of many types"
uScheme provides primitive = that works on numbers, symbols, and Booleans, but never cons cells.
It is useful only for comparing atoms
Let's define equal?, which will identify isomorphic S-expressions, including lists as a special case.
Look at slide: what are the cases?
*** Atoms and polymorphic equality (on SX) ***
(define atom? (x)
(or (number? x)
(or (symbol? x)
(or (boolean? x)
(null? x)))))
(define equal? (s1 s2)
(if (or (atom? s1) (atom? s2))
(= s1 s2)
(and (equal? (car s1) (car s2))
(equal? (cdr s1) (cdr s2)))))
What's hard: moving from a sequence of operations on elements to a single operation on a list. The good news: this is also your leverage.
Board:
- induction principle for lists
Sequential composition is associative:
xs .. e = xs
e .. ys = ys
(x .. xs) .. ys = x .. (xs .. ys)
xs .. (y .. ys) = (xs .. y) .. ys
That double dot is informal (advantage to the mathematicians)
Identify the dots
We don't have snoc
Which equations look useful for writing append?
Review:
User-defined functions:
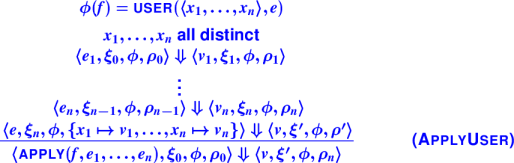
User-defined functions:

Question: why do we break code up into functions?
Proper documentation therefore looks like this:
Because the program does not contain set, parameters and results are sufficient---there is nothing else you have to understand.
Faults to correct when you write your uScheme homework:
Write fewer helper functions
Make sure each helper function has a contract
Avoid narrative description of a sequence of events ("counts up", "searches", and so on)
Ideally, write one line mentioning each parameter and the result
(if (= 0 (gcd m n)) 1 0) should be written how?
Individual feedback is coming...
Board:
Using informal math notation, with .. for "followed by", we have these laws:
xs .. e = xs
e .. ys = ys
(x .. xs) .. ys = x .. (xs .. ys)
xs .. (y .. ys) = (xs .. y) .. ys
The underlying operations are append, cons, and snoc
But we have no snoc
If we cross out the snoc law, we are left with three cases... but case analysis on the first argument is complete.
So cross out the law xs .. e == xs.
What is it in Scheme notation? (See slide)
*** Equations and function for append ***
(append '() ys) == ys
(append (cons z zs) ys) == (cons z (append zs ys))
(define append (xs ys)
(if (null? xs) ys
(cons (car xs) (append (cdr xs) ys))))
Why does it terminate?
Other laws:
(append (list1 x) ys) = ???
Allocation is the big cost.
How many cons cells are allocated?
What about list reversal?
reverse '() = '()
reverse (x .. xs) = reverse xs .. reverse x = reverse xs .. x
And the code?
*** Naive list reversal ***
(define reverse (xs)
(if (null? xs) '()
(append (reverse (cdr xs))
(list1 (car xs)))))
How many cons cells are allocated?
Let's try a new algebraic law:
reverse (x .. xs) .. zs = reverse xs .. x .. zs = reverse xs .. (cons x zs)
reverse '() .. zs = zs
The code
*** Reversal by accumulating parameters ***
(define revapp (xs zs)
(if (null? xs) zs
(revapp (cdr xs) (cons (car xs) zs))))
(define reverse (xs) (revapp xs '()))
Parameter zs is the accumulating parameter.
(A powerful, general technique.)
Implementation: list of key-value pairs
'((k1 v1) (k2 v2) ... (kn vn))
Picture with spine of cons cells, car, cdar, caar, cadar.
*** A-list example ***
-> (find 'Building '((Course 105) (Building Lane)
(Instructor Ramsey)))
Lane
-> (val nr (bind 'Office 'Extension-006
(bind 'Courses '(105)
(bind 'Email 'comp105-staff '()))))
((Email comp105-staff) (Courses (105)) (Office Extension-006))
-> (find 'Office nr)
Extension-006
-> (find 'Favorite-food nr)
()
Notes:
- attribute can be a list or any other value
- 'nil' stands for 'not found'
*** Laws of assocation lists ***
(find k (bind k v l)) = v
(find k (bind k' v l)) = (find k l), provided k != k'
(find k '()) = '() --- bogus!
Why are lists so useful?
Sequences a frequently used abstraction
Can easily approximate a set
Can implement finite maps with association lists
You don't have to manage memory
These "cheap and cheerful" representations are less efficient than balanced search trees, but are very easy to implement and work with---see the book.
The only thing new here is automatic memory management. Everything else you could do in C. (You can have automatic memory management in C as well.)
One easy and one hard
let binding for local names
First-class, nested, higher-order functions
*** Introduce local names into environment ***
(let ((x1 e1)
...
(xn en))
e)
Evaluate e1 through en, bind answers to x1, ... xn
- Name intermediate results (simpler code, less error prone)
Creates new environment for local use only:
rho {x1 |-> v1, ..., xn |-> vn}
Also let* (one at a time) and letrec (local recursive functions)
Note that we really have definititions and it might be easier to read if McCarthy had actually used definition syntax, which you'll see in ML, Haskell, and other functional languages:
*** What McCarthy should have done ***
(let ((val x1 e1)
...
(val xn en))
e)
Things that should offend you about Impcore:
Look up function vs look up variable requires different interfaces!
To get a variable, must check 2 or 3 environments.
- Can't create a function without giving it a name:
- High cognitive overhead
- A sign of second-class citizenship
All these problems have one solution: lambda
From Church's lambda-calculus:
(lambda (x) (+ x x))
"The function that maps x to x plus x"
At top level, like define. (Or more accurately, define is a synonym for lambda.)
In general, \x.E or (lambda (x) E)
x is bound in E- other variables are free in
E
The ability to "capture" free variables is what makes it interesting:
(lambda (x) (+ x y)) ; means what??
What matters is that y can be a parameter or let-bound variable of an enclosing functions.
- Can tell at compile time what is captured.
- To understand why anyone cares, you'll need examples
First example: finding roots
*** Function escapes! ***
-> (define to-the-n-minus-k (n k)
(let
((x-to-the-n-minus-k (lambda (x)
(- (exp x n) k))))
x-to-the-n-minus-k))
-> (val x-cubed-minus-27 (to-the-n-minus-k 3 27))
-> (x-cubed-minus-27 2)
-19
to-the-n-minus-k is a higher-order function because it returns another (escaping) function as a result.
*** No need to name the escaping function ***
-> (define to-the-n-minus-k (n k)
(lambda (x) (- (exp x n) k)))
-> (val x-cubed-minus-27 (to-the-n-minus-k 3 27))
-> (x-cubed-minus-27 2)
-19
*** Application: a zero-finder ***
(define findzero-between (f lo hi)
; binary search
(if (>= (+ lo 1) hi)
hi
(let ((mid (/ (+ lo hi) 2)))
(if (< (f mid) 0)
(findzero-between f mid hi)
(findzero-between f lo mid)))))
(define findzero (f) (findzero-between f 0 100))
findzero-between is also a higher-order function because it takes another function as an argument. But nothing escapes; you can do this in C.
*** Cube root of 27 and square root of 16 ***
-> (findzero (to-the-n-minus-k 3 27))
3
-> (findzero (to-the-n-minus-k 2 16))
4

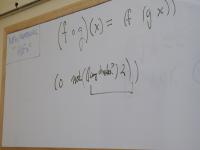
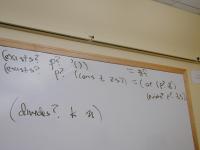
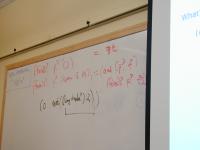
Notes on where we've been, where we're going:
lecture is covering the hard bits only; we've focused on developing code guided by case analysis over the data
if we're an airplane, the nose wheel is just coming up
talk about solutions Wednesday
Why this matters: if you have nested, escaping functions, you can apply all the programming technique you're about to learn
Go back to integers; they're simpler
*** Review: an "escaping" function ***
-> (define to-the-n-minus-k (n k)
(lambda (x) (- (exp x n) k)))
"Escape" means "outlive the activation in which the lambda was evaluated."
Escaping and lifetimes are some of those universal decisions every programmer has to think about.
Where are n and k stored???
- Values that escape have to be allocate on the heap
C programmers do this explicitly with malloc
In a language with first-class, nested functions, part of the semantics of lambda
Escaping function represented by a closure:

*** What's the picture for conjunction? ***
(define conjoin (p? q?)
(lambda (x) (if (p? x) (q? x) #f)))
Preview: in math, what is the following equal to?
(f o g)(x) == ???
Another algebraic law, another function:
*** Functions create new functions ***
-> (define o (f g) (lambda (x) (f (g x))))
-> (define even? (n) (= 0 (mod n 2)))
-> (val odd? (o not even?))
-> (odd? 3)
-> (odd? 4)
Don't forget `(o not null?)'
*** Classic functional technique: Currying ***
-> (val positive? (lambda (y) (< 0 y)))
-> (positive? 3)
-> (val <-curried (lambda (x) (lambda (y) (< x y))))
-> (val positive? (<-curried 0))
; "partial application"
-> (positive? 0)
No need to Curry by hand!:

No need to Curry by hand!:

What's the algebraic law for curry?
... (curry f) ... = ... f ...
Keeping in mind all you can do with a function is apply it?
*** Bonus content: vulnerable variables? ***
-> (val seed 1)
-> (val rand (lambda ()
(set seed (mod (+ (* seed 9) 5) 1024)))))
-> (rand)
14
-> (rand)
131
-> (set seed 1)
1
-> (rand)
14
*** Bonus: Lambda as abstraction barrier! ***
-> (val mk-rand (lambda (seed)
(lambda ()
(set seed (mod (+ (* seed 9) 5) 1024))))))
-> (val rand (mk-rand 1))
-> (rand)
14
-> (rand)
131
-> (set seed 1)
error: set unbound variable seed
-> (rand)
160
Q: Can you do case analysis on a function?
A: No!
Q: So what can you do then?
A: Apply it!
Examples
Recursive function consuming A is related to proof about A
Q: How to prove two lists are equal?
A: Prove they are both nil or that they are both cons cells cons-ing equal car's to equal cdr's
Q: How to prove two functions equal?
A: Prove that when applied to equal arguments they produce equal results.
What we did last time:
Make functions from other functions (Exactly related to your homework problem 15: sets as functions. "Make sets from other sets" is now the same as "make functions from other functions".
Will also show up as part of several other homework problems.
What's coming on homework
Huge fraction of homework involves standard list functions (today)
Monday, continuation-passing style (the formula solver)
Goal: start with functions on elements, wind up with functions on lists
- This goal generalizes to sets, arrays, search trees, hash tables, and what have you
Capture common patterns of computation or algorithms
exists?, all? (is there a number?)filter (take only the numbers?)map (add 1 to every element)- foldr (general)
Folds also called reduce, accum, "catamorphism"
Algorithm encapsulated: linear search
Algebraic law on the board:
(exists? p? '()) == ???
(exixts? p? '(cons a as)) == ???
*** SLIDE ***
-> (define exists? (p? xs)
(if (null? xs)
(if (p? (car xs))
(exists? p? (cdr xs)))))
-> (exists? pair? '(1 2 3))
-> (exists? pair? '(1 2 (3)))
-> (exists? ((curry =) 0) '(1 2 3))
-> (exists? ((curry =) 0) '(0 1 2 3))

Quiz friday: satisfying assignments to Boolean formulas
Problem: Give me a list of numbers; return only the even elements.
What are the laws?
(filter even? '()) == ???
(filter even? '(cons m ms)) == ???
*** SLIDE ***
-> (define filter (p? xs)
(if (null? xs)
'()
(if (p? (car xs))
(cons (car xs) (filter p? (cdr xs)))
(filter p? (cdr xs)))))
-> (filter (lambda (n) (> n 0)) '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter (lambda (n) (<= n 0)) '(1 2 -3 -4 5 6))
(-3 -4)
-> (filter ((curry <) 0) '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter ((curry >=) 0) '(1 2 -3 -4 5 6))
(-3 -4)
*** List filtering: composition revisited ***
-> (val positive? ((curry <) 0))
<procedure>
-> (filter positive? '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter (o not positive?) '(1 2 -3 -4 5 6))
(-3 -4)
Algorithm encapsulated: do this to every element
Problem: square every element of a list.
What are the laws?
(map square '()) ==
(map square (cons n ns)) ==
*** SLIDE ***
-> (define map (f xs)
(if (null? xs)
'()
(cons (f (car xs)) (map f (cdr xs)))))
-> (map number? '(3 a b (5 6)))
(#t #f #f #f)
-> (map ((curry *) 100) '(5 6 7))
(500 600 700)
-> (val square* ((curry map) (lambda (n) (* n n))))
<procedure>
-> (square* '(1 2 3 4 5))
(1 4 9 16 25)
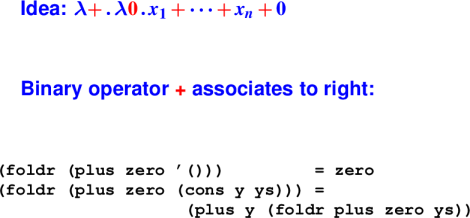

Another view of operator folding:
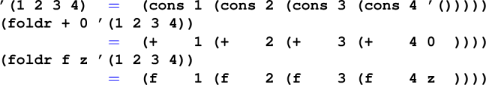
foldr is a catamorphism
- Any recursively defined data type has one!
Another catamorphism: foldl associates to left
How to handle
(take n xs)
What is the case analysis?
(take 0 '()) ==
(take 0 (cons z zs)) ==
(take (+ n 1) '()) ==
(take (+ n 1) (cons z zs)) ==
Proof about functions:
((flip f) x y) = (f y x)
(o flip flip)

Must get to solver today (before long weekend)
A call in tail position.
What is tail position?
Tail position is defined inductively:
- The body of a function is in tail position
- When
(if e1 e2 e3) is in tail position, so are e2 and e3
- When
(let (...) e) is in tail position, so is e, and similary for letrec and let*.
- When
(begin e1 ... en) is in tail position, so is en.
Idea: the last thing that happens
Anything in tail position is the last thing executed!
Key idea is tail-call optimization!
Tail-call optimization:

Example of tail position:

Example of tail position:
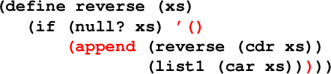
Question: how much stack space is used by the call?
Another example of tail position:
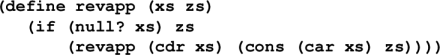
Another example of tail position:

Question: how much stack space is used by the call?
Question: in your previous life, what did you call a construct that
- Transfers control to an arbitrary point in the code?
- Uses no stack space?
Direct style - last action is to return a value
Continuation-passing style - last action is to "throw" value to a continuation
- Not like a call (it never returns)
- Think "goto with arguments"
Simulate with a tail call.
How functions finish:
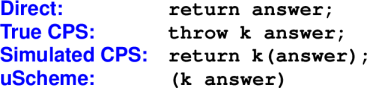
Problem in interface design:

Ideas?
Bad choices:
- nil
- special symbol
'fail
- run-time error
Good choice:
- exception (not in uScheme)
Solution: new interface:

*** Coding \lit{witness} with continuations ***
(define witness-cps (p? xs succ fail)
(if (null? xs)
(fail)
(let ((x (car xs)))
(if (p? x)
(succ x)
(witness-cps p? (cdr xs) succ fail)))))
Tail calls: continuations, recursion:

Question: how much stack space is used by the call?
Example use: instructor lookup:

*** Simple continuations at work ***
-> (val 2012s '((Ramsey 105)(Hescott 170)(Chow 116)))
-> (instructor-info 'Ramsey 2012s)
(Ramsey teaches 105)
-> (instructor-info 'Chow 2012s)
(Chow teaches 116)
-> (instructor-info 'Souvaine 2012s)
(Souvaine is-not-on-the-list)
{Continuations for search problems}:

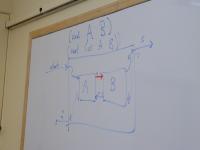
{Continuations for the solver}:

First wireup: we must solve both A and B
Solver enters A
If A is solved, newly allocated success continuation starts B
If B succeeds, we're done! Use continuation from context.
If B fails, it resumes A using the resumption continuation passed.
If ever A fails, the whole thing fails. Use continuation from context.
Only one new continuation is allocated
Second wireup: it's enough to solve either A or B
Solver enters A
If A is solved, we're good! But what if context doesn't like solution? It will automatically resume A using the resume continuation passed in.
If A is not solved, don't give up! Try a newly allocated failure continuation. This one starts B.
If ever B is started, we've given up on A entirely. So B's success and failure continuations are exactly the ones in the context.
If B succeeds, the context can resume it.
If B fails, abject failure all around.
For a recap, you can see an old video. The video is not bad, but it is wrong about the number of continuations that need to be allocated. As shown in the notes above, only one continuation needs to be allocated in each unit.
Concluding remark (board): functions are cheap

Analyze uScheme from the semantic point of view
Pull back for slightly broader perspective on uScheme (end of part I)
Part II: examples from your uScheme code and how to improve them; communicating higher aspirations for your code (maybe?)
First three of five questions: Syntax, values, environments
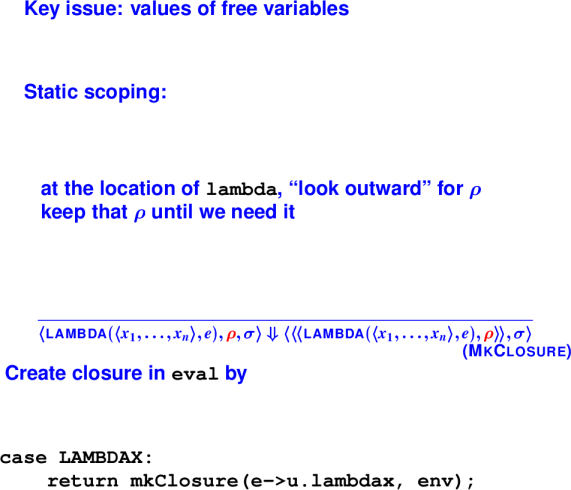
Key changes from Impcore
New constructs: let, lambda, application (not just names)
New values, including functions (closures)
A single environment
Environments get copied
Environment maps names to mutable locations, not values
{ vs }:

{Evaluation judgment}:

{Evaluation rules}:
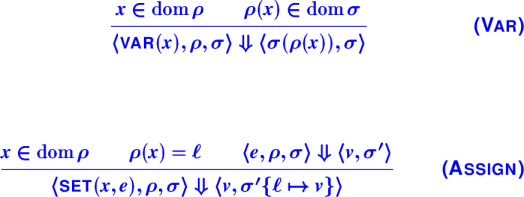
{Implementation of closures}:
{Applying closures}:

{Locations in closures}:

Closure optimizations
{ and the Five Questions}:

Common Lisp, Scheme:
- Big environments, tiny interpreters, everything between
- High-level data structures
- Cheap, easy recursion
- Automatic memory management (garbage collection!)
- Programs as data!
- Sophisticated Interactive Development Environments
Down sides:
- Hard to talk about data
- Hard to detect errors at compile time
Bottom line: it's all about lambda
- Major win
- Real implementation cost (heap allocation)
Many of you are doing much better on naming and contracts.
On the HOFs homework due Friday, failing grades for helper functions without contracts.
Homework review
Good, bad, and things to avoid
*** Classic mirror --- two case analyses ***
(define mirror (xs) ; xs in LIST(SEXP)
(if (null? xs)
xs
(if (atom? (car xs)) ; (car xs) in SEXP
(append (mirror (cdr xs)) (list1 (car xs)))
(append (mirror (cdr xs)) (list1 (mirror (car xs)))))))
*** Improvement 1 --- no duplicate code ***
(define mirror (xs) ; xs in LIST(SEXP)
(if (null? xs)
xs
(append (mirror (cdr xs))
(list1 (if (atom? (car xs))
(car xs)
(mirror (car xs))))))))
; 'if' has been pushed inside the call
*** Improvement 2 --- $\mathit{LIST}(\mathit{SEXP}) \subset \mathit{SEXP}$ ***
(define mirror (xs) ; xs in SEXP
(if (atom? xs) ; just one case analysis
xs
(append (mirror (cdr xs))
(list1 (mirror (car xs))))))
*** Improvement 3 --- alternate case analysis ***
(define mirror (xs) ; xs in SEXP
(if (pair? xs)
(append (mirror (cdr xs))
(list1 (mirror (car xs))))
xs))
*** Advanced version using HOFs ***
(define mirror (x)
(if (atom? x)
x
(reverse (map mirror x))))
*** Flatten (excessive case analysis) ***
(define flatten (xs)
(if (null? xs)
xs
(if (pair? (car xs)) ; <=== RED FLAG HERE
(append (flatten (car xs)) (flatten (cdr xs)))
(if (null? (car xs))
(flatten (cdr xs))
(append (list1(car xs)) (flatten (cdr xs)))))))
*** Flatten equations --- complex form ***
(flatten '()) == '()
(flatten (cons xs ys)) == (append (flatten xs)
(flatten ys))
(flatten (cons nonlist ys)) == ; hard to test for!
(cons nonlist (flatten ys))
; lasting lesson: general S-expressions harmful
*** Flatten equations --- simple form ***
(flatten '()) == '()
(flatten atom) == (list1 atom) ; non-nil
(flatten (cons v1 v2)) == (append (flatten v1)
(flatten v2))
*** Flatten (case analysis on xs only) ***
(define flatten (xs) ; xs in SEXP
; return list of atoms in xs
(if (null? xs)
'()
(if (pair? xs)
(append (flatten (car xs)) (flatten (cdr xs)))
(list1 xs))))
*** Flatten (accumulating parameters) ***
(define flatten-append (xs ys)
; returns (append (flatten xs) ys)
(if (pair? xs)
(flatten-append (car xs)
(flatten-append (cdr xs) ys))
(if (null? xs) ys
(cons xs ys))))
(define flatten (xs)
(flatten-append xs '()))
*** Red flag: testing \lit{length} for equality ***
(define mirror (xs)
(if (atom? xs) xs
(if (= 1 (length (cons (car xs) '())))
(append (mirror (cdr xs))
(cons (mirror (car xs)) '()))
(cons (mirror (cdr xs))
(mirror (cons (car xs) '()))))))
*** Red flag eliminated ***
(define mirror (xs)
(if (atom? xs) xs
(append (mirror (cdr xs))
(cons (mirror (car xs)) '()))
*** Name this predicate ***
; lists xs and ys in scope---what's happening?
(if (equal? xs (take (length xs) ys))
...
...)
*** Wait for it ***
...
*** Specification of \lit{prefix?} predicate ***
(prefix? '() '()) == #t
(prefix? '() (cons y ys)) == #t
(prefix? (cons x xs) '()) == #f
(prefix? (cons x xs) (cons y ys)) == x = y
&& (prefix? xs ys)
*** Proper \lit{prefix?} predicate ***
(define prefix? (needle haystack)
(if (null? needle)
(if (null? haystack)
(if (= (car needle) (car haystack))
(prefix? (cdr needle) (cdr haystack))
;
; does not allocate and is quick to answer #f
bv - Largest element of a singleton list? (if (null? (cdr as)) (max* as) ...) ev
*** Largest element of a singleton list? ***
(if (null? (cdr as))
(car as)
...)
*** What's an empty list? ***
(if (= (length xs) 0)
...
...
)
*** What's an empty list? ***
(if (null? xs)
...
...
)
*** Evil layout for if-expressions ***
(if ....... ..............
.......)
*** Good layouts for if-expressions ***
(if .... ......... ........)
(if ....
..........
.......)
*** Some acceptable if-expressions ***
(if ..... 0
..........)
(if ..... '()
..........)
*** Single-use \lit{lambda} ***
((lambda (xs) (rstack '() xs)) (car rest))
*** Better ***
((lambda (xs) (rstack '() xs)) (car rest))
(let ((xs (car rest))) (rstack '() xs))
*** Best ***
((lambda (xs) (rstack '() xs)) (car rest))
(let ((xs (car rest))) (rstack '() xs))
(rstack '() (car rest)))
*** What's wrong here? ***
(define takewhile (p xs)
(let*
((it (if (atom? xs)
xs
(if (p (car xs))
(cons (car xs) (takewhile p (cdr xs)))
(takewhile p (cdr xs))))))
it))
*** Fix it ***
(let* ((it e)) it) == e
(define takewhile (p xs)
(if (atom? xs)
xs
(if (p (car xs))
(cons (car xs) (takewhile p (cdr xs)))
(takewhile p (cdr xs)))))
- Macros!
- Cond expressions (solve nesting problem)
- Mutation
- Garbage collection
- Tail calls
- Applications and assessment
A Scheme program is just another S-expression
- Define functions that manipulate them at compile time
- Macro hygiene ensures macro parameters don't interfere with program variables
- Used to implement
and, let, others...
*** Real Scheme Conditionals ***
(cond (c1 e1) ; if c1 then e1
(c2 e2) ; else if c2 then e2
... ...
(cn en)) ; else if cn then en
; Syntactic sugar---'if' is a macro:
(if e1 e2 e3) == (cond (e1 e2)
(#t e3))
Real Scheme: macros
A Scheme program is an S-expression
Function define-syntax manipulates syntax at compile time
Macros are hygienic---name clashes impossible
let, and, many others implemented as macros
Real Scheme: mutation
Not only variables can be mutated
Mutate heap-allocated cons cell:
(set-car! '(a b c) 'd) => (d b c)
Circular lists, sharing, avoids allocation
- still for specialists only
Apply your new knowledge in Standard ML:
- You've already learned the ideas
- There will be a lot of new detail
Much less intellectual effort
New homework, and a different kind of effort:
- Only one new idea is required, and you will like it
- A second new idea is mostly optional
- A ton of new details
- No hard thinking, but a lot of reading and looking things up
Lectures on ML:
- Algebraic types and pattern matching
- A touch of types
- Everything else
Meta: Not your typical introduction to a new language
- Not definition before use, as in a manual
- Not tutorial, as in Ullman
- Instead, the most important ideas that are most connected to your work up to now
ML Overview
Designed for programs, logic, symbolic data
Theme: talking about data
Board: ML = uScheme + pattern matching + exceptions + static types
Three new ideas:
- Pattern matching is big and important. You will like it.
- Exceptions are easy
- Static types get two to three weeks in their own right.
And lots of new concrete syntax!
Board: Let's do some examples
cons is infix ::
nil is []
Somebody give me a list function from uScheme
What are the equations?
length [] = 0
length (x::xs) = 1 + length xs
How do we make it code? Add fun and a bar
- Try it in the interpreter
Things to notice:
No brackets! (I hate the damn parentheses)
Function application by juxtaposition
Function application has higher precedence than any infix operator
Compiler checks all the cases (try in the interpreter)
Let's try another? map, filter, exists, all, take, drop, takewhile, dropwhile?
composition of two maps?
ML---The Five Questions
Syntax: expressions, definitions, patterns, types
Values: num/string/bool, record/tuple,
Environments: names stand for values (and types)
Evaluation: uScheme + case and pattern matching
Initial Basis: medium size; emphasizes lists
(Question Six: type system---a coming attraction)
A note about books
Ullman is easy to digest
Ullman is clueless about good style
Suggestion:
- Learn the syntax from Ullman
- Learn style from Ramsey
(My style is not flawless---some Haskell style has crept in---but it will serve you better than Ullman. And I've made some effort at consistency.)
Tidbits:
The most important idea in ML!
Originated with Hope (Burstall, MacQueen, Sannella), in the same lab as ML, at the same time (Edinburgh!)
(Wikipedia article among the worst ever.)
Board:
A "Boolean" is produced using true or false
A "list of A" is produced using nil or a :: as, where a is an A and as is a "list of A"
A "Heap of A" is either empty or it's an A and two child heaps
Exegesis (on board):
Notation 'a is a type variable
- On left-hand side, it is a formal type parameter
- On right-hand side it is an ordinary type
- In both cases it represents a single unknown type
Name before = introduces a new type constructor into the type environment. Type constructors may be nullary.
Alternatives separated by bars are value constructors of the type
They are new and hide previous names
(Do not hide built-in names list and bool from the initial basis!)
Value constructors participate in pattern matching
Complete by themselves: true, false, nil
Expect parameters to make a value or pattern: ::, HEAP
op enables an infix operator to appear in a nonfix context
Type application is postfix
- On last line,
'a heap is the type parameter to list
New names into two environments:
bool, list, heap stand for new type constructors
true, false, nil, ::, EHEAP, HEAP stand for new value constructors
Algebraic datatypes are inherently inductive (list appears in its own definition)---to you, that means finite trees
'a * 'a list is a pair type --- infix operators are always applied to pairs
*** SLIDE ***
datatype bool = true | false (* copy me NOT! *)
datatype 'a list = nil (* copy me NOT! *) | op :: of 'a * 'a list
datatype 'a heap = EHEAP | HEAP of 'a * 'a heap * 'a heap
type bool val true : bool type 'a list val false : bool type 'a heap val nil : forall 'a . 'a list val op :: : forall 'a . 'a * 'a list -> 'a list val EHEAP : forall 'a . 'a * 'a heap * 'a heap -> 'a heap val HEAP : forall 'a . 'a heap
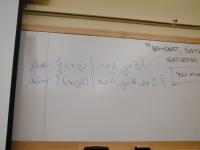




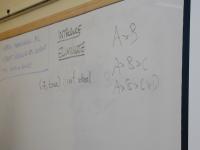
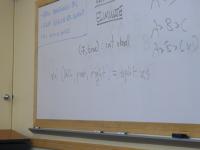

Background for datatype review (board):
if A and B are sets, what is A * B?
if A and B are sets, what is A -> B?
if A, B, and C are sets, what is A * B * C?
This is all you need to know about the special built-in type constructors (cross and arrow).
Algebraic datatype review:
Frequently overlooked
An algebraic data type is a collection of alternatives
Don't forget:
- Each alternative must have a name
The thing named is the value constructor
(Also called "datatype constructor")
*** SLIDE ***
datatype bool = true | false (* copy me NOT! *)
datatype 'a list = nil (* copy me NOT! *)
| op :: of 'a * 'a list
datatype 'a heap = EHEAP
| HEAP of 'a * 'a heap * 'a heap
type bool val true : bool
type 'a list val false : bool
type 'a heap val nil : forall 'a . 'a list
val op :: : forall 'a .
'a * 'a list -> 'a list
val EHEAP : forall 'a . 'a * 'a heap * 'a heap -> 'a heap
val HEAP : forall 'a . 'a heap
Exegesis (on board):
Notation 'a is a type variable
- On left-hand side, it is a formal type parameter
- On right-hand side it is an ordinary type
- In both cases it represents a single unknown type
Name before = introduces a new type constructor into the type environment. Type constructors may be nullary.
Alternatives separated by bars are value constructors of the type
Value constructors participate in pattern matching
Complete by themselves: true, false, nil
Expect parameters to make a value or pattern: ::, HEAP
Type application is postfix
- On last line,
'a heap is the type parameter to list
New names into two environments:
bool, list, heap stand for new type constructors
true, false, nil, ::, EHEAP, HEAP stand for new value constructors
Algebraic datatypes are inherently inductive (list appears in its own definition)---to you, that means finite trees
Eliminate values of algebraic types
New language construct case (an expression)
fun length xs =
case xs
of [] => 0
| (x::xs) => 1 + length xs
At top level, better than
When possible, write
fun length [] = 0
| length (x::xs) = 1 + length xs
"Syntactic sugar"
Part of learning any new field: talk to people in their native vocabulary
Introduce means "produce", "create", "make", "define"
Eliminate means "consume", "examine", "observe", "use"
It's like knowing what to say when somebody sneezes.
Types and their uses:
|
Type
|
Produce
|
Consume
|
|
Introduce
|
Eliminate
|
|
arrow
|
Lambda (fn)
|
Application
|
|
algebraic
|
Apply constructor
|
Pattern match
|
|
tuple
|
(e1, ..., en)
|
Pattern match!
|
Example pattern match on a tuple:
val (left, pivot, right) = split xs
The types survey:
Baffling Noise I can ignore Information I understand
Today, add to far right: type help me program
- (Possible bonus content: ML traps and pitfalls)
Common idea in functional programming: "lifting:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
do the example
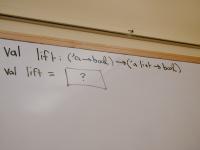

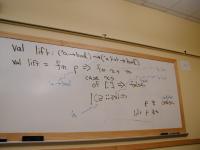
Quiz question:
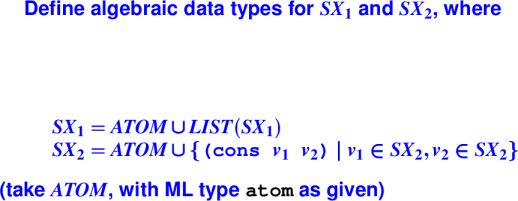
Wait for it ...
*** Quiz answers ***
datatype sx1 = ATOM1 of atom
| LIST1 of sx1 list
datatype sx2 = ATOM2 of atom
| PAIR2 of sx2 * sx2
Plan for today:
Finish the lift example (slide for context)
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
The people's choice:
Types and their ML constructs:

*** Type-directed coding (review) ***
val lift : ('a -> bool) -> ('a list -> bool)
fun lift p = (fn xs => (case xs
of [] => false
| z::zs => p z orelse
lift p zs))
*** Merge top-level \lit{fn} into \lit{fun} ***
fun lift p xs = case xs of [] => false
| z::zs => p z orelse
lift p zs
*** Merge top-level \lit{case} into \lit{fun} ***
fun lift p [] = false
| lift p (z::zs) = p z orelse lift p zs
*** I know this function! ***
fun exists p [] = false
| exists p (z::zs) = p z orelse exists p zs
*** Heap insertion ***
datatype 'a heap = EHEAP
| HEAP of 'a * 'a heap * 'a heap
val insert : int * int heap -> int heap
Alert! Balance invariant...
ML Traps and pitfalls:

Integer literals as patterns, overlapping patterns
*** Order of clauses matters ***
fun take n (x::xs) = x :: take (n-1) xs
| take 0 xs = []
| take n [] = []
(* what goes wrong? *)
Gotcha - Value polymorphism:
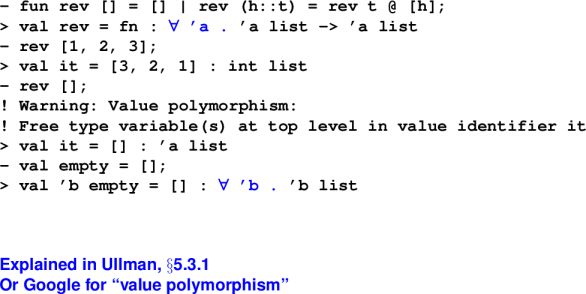
*** Gotcha --- overloading ***
- fun plus x y = x + y;
> val plus = fn : int -> int -> int
- fun plus x y = y + y : real;
> val plus = fn : real -> real -> real
Gotcha --- equality types:
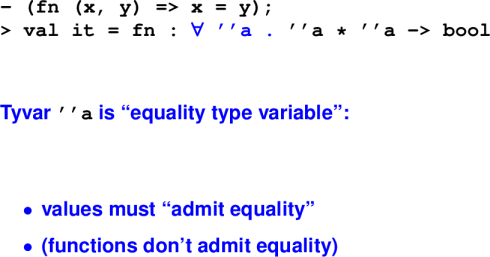
Gotcha --- parentheses
Put parentheses around anything with |
case, handle, fn
Function application has higher precedence than any infix operator
Gotcha --- fixity
Fixity:
infixr 5 @ (* associativity, precedence *)
Revert using op
*** Lists and fixity ***
- [+, -, *, div];
! Toplevel input:
! [+, -, *, div];
! ^
! Ill-formed infix expression
- [op +, op -, op *, op div];
> val it = [fn, fn, fn, fn] : (int * int -> int) list
- length it;
> val it = 4 : int
-
*** Syntactic sugar for lists ***
- 1 :: 2 :: 3 :: 4 :: nil; (* :: associates to the right *)
> val it = [1, 2, 3, 4] : int list
- "the" :: "ML" :: "follies" :: [];
> val it = ["the", "ML", "follies"] : string list
> concat it;
val it = "theMLfollies" : string
Another example:
val map: forall 'a, 'b . ('a -> 'b) -> ('a list -> 'b list)
Do map on the board
Use fun syntax for Currying
*** Code for a function consuming lists ***
fun map f [] = []
| map f (x::xs) = f x :: map f xs
(* FUNCTION APPLICATION HAS HIGHER
PRECEDENCE THAN ANY INFIX OPERATOR! *)
More examples:
Option.map
filter
flatten (with sx1)
curry flip infixr 0 $
uncurry fst
snd
Bonus: running ML
To run Moscow ML:
ledit mosml -P full
And tell it:
help "";
use "warmup.sml";
Also /usr/bin/sml, /usr/bin/mlton
ML from 10,000 feet:

The value environment
Names bound to immutable values
(Immutable ref and array values point to mutable locations
ML has no binding-changing assignment
Definitions add new bindings (hide old ones):
val pattern = exp
val rec pattern = exp
fun ident patterns = exp
datatype ... = ...
Nesting environments
At top level, definitions
Definitions contain expressions:
def ::= val pattern = exp
Expressions contain definitions:
exp ::= let defs in exp end
Sequence of defs has let-star semantics
What is a pattern?
pattern ::= variable
| wildcard
| value-constructor [pattern]
| tuple-pattern
| record-pattern
| integer-literal
| list-pattern
Design bug: no lexical distinction between
- VALUE CONSTRUCTORS
- variables
Workaround: programming convention
Function pecularities: 1 argument
Each function takes 1 argument, returns 1 result
For "multiple arguments," use tuples!
fun factorial n =
let fun f (i, prod) =
if i > n then prod else f (i+1, i*prod)
in f (1, 1)
end
fun factorial n = (* you can also Curry *)
let fun f i prod =
if i > n then prod else f (i+1) (i*prod)
in f 1 1
end
Tuples are "usual and customary."
Mutual recursion:

Syntax of ML types:

Syntax of ML types:

Polymorphic types:

Old and new friends:
Board:
Syntax:
raise E where E : exn- Example:
exception EmptyQueue
Semantics:
- alternative to normal termination
- can happen to any expression
- tied to function call
- if evaluation of body raises exn, call raises exn
Handler uses pattern matching
e handle pat1 => e1 | pat2 => e2
*** Exception handling in action ***
loop (evaldef (reader (), rho, echo)) handle EOF => finish () | Div => continue "Division by zero" | Overflow => continue "Arith overflow" | RuntimeError msg => continue ("error: " ^ msg) | IO.Io {name, ...} => continue ("I/O error: " ^ name) | SyntaxError msg => continue ("error: " ^ msg) | NotFound n => continue (n ^ "not found")
*** SLIDE ***
val filter : forall 'a . ('a -> bool) ->
'a list -> 'a list
fun filter p [] = []
| filter p (x::xs) =
case p x
of true => x :: filter p xs
| false => filter p xs
fun filter p [] = []
| filter p (x::xs) =
if p x then x :: filter p xs
else filter p xs
Flattening S-expressions
Let's not care what an atom is
datatype 'a sxl = SXLEAF of 'a
| SXLIST of 'a sxl list
Exercise --- write
val flatten : forall 'a . 'a sxl -> 'a list
*** SLIDE ***
fun flatten (SXLEAF a) = [a]
| flatten (SXLIST ts) = (List.concat o map flatten) ts
fun flatten (SXLEAF a) = [a]
| flatten (SXLIST ts) = List.concat (map flatten ts)
fun flatten t =
let fun flatapp (SXLEAF a, tail) = a :: tail
| flatapp (SXLIST ts, tail) =
foldr flatapp tail ts
in flatapp (t, [])
end





The midterm exam:
In class, next Wednesday
Operational semantics and functional programming
Count on some proof, some semantics, some code (code can be in uScheme or in ML)
A little review Monday
I will hold office hours Tuesday before the exam
Review homework solutions
Preparing for the midterm review on Monday (Followup March 15)
What kind of value do we have?
n + 1
"hello" ^ "world"
(fn n => n * (n - 1))
if p then 1 else 0
if true then 1 else 0
Questions type systems can answer:
What kind of value does it evaluate to (if it terminates)?
Who has the rights to look at it?
Is the number miles or millimeters?
What is the contract of the function (!)
How can I parse this data (to detect fraud)?
Source of new language ideas for next 20 years
Needed if you want to understand advanced designs (or create your own)
Q: What context do we need to evaluate an expression?
Q: Do we need all the same context to decide on a type?
Q: What do we need then?
Define a datatype for expressions with
- Simple integer arithmetic operations
- Numeric comparisons
- Conditional
- Numeric literal
Language of expressions
Numbers and Booleans:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| IF of exp * exp * exp
| LIT of int
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = INTTY | BOOLTY
What's the type of an expression?
Form of judgment context |- term : type
Written |- e : tau
Contexts vary between type systems
(Right now, the empty context)
What proof system do you recommend for this language?
How do we code val ty : exp -> ty?
Given e, find tau such that |- e : tau
What is a type?
As a working definition, a set of values
As a precise definition, a classifier for terms!!
- Note: a computation can have a type even if it never produces a value!



Where have we been?
- I gave you the syntax, but you came up with the typing rules
Where are we going?
This is a big chunk of what language designers do.
Board: rules developed for ARITH, CMP, LIT
Board: placeholder for IF
(Show syntax on slide)
Language of expressions
Numbers and Booleans:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| IF of exp * exp * exp
| LIT of int
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = INTTY | BOOLTY
Develop rule for IF
Write the code
An implementor's trick: If you see identical types in a rule,
Give each type a distinct subscript
Introduce equality constraints
Remember to be careful using primitive equality to check types---you are better off with eqType.
Add variables and let binding to our language, what happens?
Type environment Gamma
What are the rules for let and VAR?
Type checker needs Gamma -- gives type of each "term variable".
How do we code let and VAR?
Ideas:
What to expect on the exam:
You can bring one page of notes, both sides
Balance of theory and code
If your exam is all one or the other, that's bad for you
Remember, understand, and apply
It's not enough to have your operational semantics written down; you have to have the ideas in your head
Notes from the homework:
Calculational proofs: don't leave out steps
Calculational proofs: do write lemmas (e.g., map-cons)
Proofs by induction
Derivations---covered in class a week before last. Compare to rho, rho' is unknown. Good only if there is an unknown derivation.
Operational semantics: read and understand new rules
Operational semantics: write rules for a new programming construct
Functional programming:
Write recursive functions by using case analysis on the structure of the data
Use standard higher-order functions to avoid creating new recursive functions
Contract for a function to mention result, parameters, and nothing about how the computation is accomplished.






New watershed in the homework
You've been developing and polishing programming skills: recursion, higher-order functions, using types to your advantage. But the problems have been all simple problems around simple data structures, mostly lists.
We're now going to shift and spend the next several weeks doing real programming-languages stuff, starting with type systems.
You've already seen everything you need to know to implement a basic type checker, and you are almost fully equipped to add array operations and types to Typed Impcore.
What's next is much more sophisticated type systems, with an infinite number of types. We'll focus on two questions:
What is and is not a good type, that is, a classifier for terms?
How shall we represent types?
We'll look at these questions in two contexts: monomorphic and polymorphic languages.
(Note on deadlines: I'm trying to get you done with type checking before break. Open to change provided it is fair to those with travel plans.)
Here's how it works:
Every new variety of type requires special syntax
We get three kinds of typing rules
Implementation is a straightforward application of what you already know.
Language designer's agenda:
What new types do I have (formation rules)
Question: If I add lists to a language, how many new types am I introducing?
What new syntax do I have to create terms of a type (introduction rules)?
What new syntax do I have to observe terms of a type (elimination rules)?
Type rules for variables:
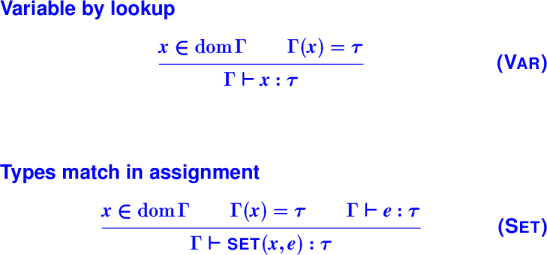
Notice: one rule for if!! (and while)
Type rules for control:

Product types: both x and y:

Pair rules generalize to product types with many elements (tuples,''structs,'' ``records'')
Arrow types: function from x to y:

Typical syntactic support for types
Explicit types on lambda and define:
For lambda, argument types:
(lambda ((int n) (int m)) (+ (* n n) (* m m)))
For define, argument and result types:
(define int max ((int x) (int y)) (if (< x y) y x))
Abstract syntax:
datatype exp = ...
| LAMBDA of (name * tyex) list * exp
...
datatype def = ...
| DEFINE of name * tyex * ((name * tyex) list * exp)
...
Array types: array of x:

Board: rules for C/C++ pointer types?
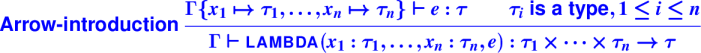
Board: Lambda rule
*** Type-checking LAMBDA ***
datatype exp = LAMBDA of (name * tyex) list * exp
...
fun ty (LAMBDA (formals, body)) =
let val Gamma' = (* body gets new env *)
foldl (fn ((n, ty), g) => bind (n, ty, g))
Gamma formals
val bodytype = typeof (body, Gamma')
val formaltypes =
map (fn (n, ty) => ty) formals
in funtype (formaltypes, bodytype)
end
Agenda for today:
Type formation: composing types
Typed Impcore:
Standard ML:
Board: type-formation ideas
Representing type constructors generically:

Monomorphic types are limiting
Each new type constructor requires
- Special syntax
- New type rules
- New internal representation (type formation)
- New code in type checker (intro, elim)
- Do another proof of soundness
Monomorphic burden: Array types:

Notes:
- Implementing arrays on homework
- Writing rules for lists on homework
Monomorphism hurts programmers too
Users can't create new syntax
User-defined functions are monomorphic:
(define int lengthI ((list int) l)
(if (null? l) 0 (+ 1 (lengthI (cdr l)))))
(define int lengthB ((list bool) l)
(if (null? l) 0 (+ 1 (lengthB (cdr l)))))
(define int lengthS ((list sym) l)
(if (null? l) 0 (+ 1 (lengthS (cdr l)))))
Next week: polymorphism!
Quantified types:

Representing quantified types
Two new alternatives for tyex:
datatype tyex
= TYCON of name
| CONAPP of tyex * tyex list
| FORALL of name list * tyex
| TYVAR of name
Kinding rules for quantified types:
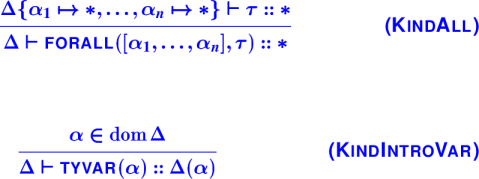
*** Substitute for quantified variables ***
-> length
<proc> : (forall ('a) (function ((list 'a)) int))
-> (@ length int)
<proc> : (function ((list int)) int)
-> (length '(1 2 3))
type error: function is polymorphic; instantiate before applying
-> ((@ length int) '(1 2 3))
3 : int
*** Substitute what you like ***
-> length
<proc> : (forall ('a) (function ((list 'a)) int))
-> (@ length bool)
<proc> : (function ((list bool)) int)
-> ((@ length bool) '(#t #f))
2 : int
*** More "Instantiations" ***
-> (val length-int (@ length int))
length-int : (function ((list int)) int)
-> (val cons-bool (@ cons bool))
cons-bool : (function (bool (list bool))
(list bool))
-> (val cdr-sym (@ cdr sym))
cdr-sym : (function ((list sym)) (list sym))
-> (val empty-int (@ '() int))
() : (list int)
Bonus instantiation:
-> map
<proc> :
(forall ('a 'b)
(function ((function ('a) 'b)
(list 'a))
(list 'b)))
-> (@ map int bool)
<proc> : (function ((function (int) bool)
(list int))
(list bool))
Create your own!
Abstract over unknown type using type-lambda
-> (val id (type-lambda ('a)
(lambda (('a x)) x)))
id : (forall ('a) (function ('a) 'a))
'a is type parameter (an unknown type)
This feature is parametric polymorphism
Board: two forms of abstraction:
|
term
|
type
|
lambda
|
function (arrow)
|
type-lambda
|
forall
|
Power comes at notational cost
Function composition
-> (val o (type-lambda ('a 'b 'c)
(lambda (((function ('b) 'c) f)
((function ('a) 'b) g))
(lambda (('a x)) (f (g x))))))
o : (forall ('a 'b 'c)
(function ((function ('b) 'c)
(function ('a) 'b))
(function ('a) 'c)))
Aka o :
Instantiate by substitution:

Generalize with type-lambda:











Instantiate by substitution:

Generalize with type-lambda:

*** A phase distinction embodied in code ***
fun checkThenEval (d, (delta, gamma, rho)) =
let val (gamma', tystring) = elabdef (d, gamma, delta)
val (rho', valstring) = evaldef (d, rho)
val _ = print (valstring ^ " : " ^ tystring)
in (delta, gamma', rho')
end
Three environments --- what happens?:
Three environments revealed:

Board exercise: term, type, value
Q: What predicts the set of values? The syntax? The type?
Q: If you see a lambda, what do you know about the value?
Q: If you see a literal, what do you know about the value?
Q: If you see an application, what do you know about the value?










Midterm evaluation note: clear that ML Syntax is something you would like improved. But the CELT people are not technical, and they were not able to articulate what sort of improvement you are looking for. If you can say something on Piazza, anonymously or otherwise, that would help us.
(Other midterm evaluation stuff: after break we will take a fresh look at TA things and at study groups, as well as other issues.)
One sophisticated idea: use fresh variable for unknown types; hold knowledge in constraints
New topic: Type inference:

*** What type inference accomplishes ***
-> (define double (x) (+ x x))
double ;; uScheme
-> (define int double ((int x)) (+ x x))
double : (function (int) int) ;; Typed uSch.
-> (define double (x) (+ x x))
double : int -> int ;; uML
*** What else type inference accomplishes ***
-> ((@ cons bool) #t ((@ cons bool) #f (@ '() bool)))
(#t #f) : (list bool) ;; typed uScheme
-> ( cons #t ( cons #f '() ))
(#t #f) : bool list ;; uML
Key ideas:
For each unknown type, introduce a fresh type variable
Enforce equality constraints
Introduce type-lambda at let/val bindings
N.B. Book is "constraints first;" lecture will be "type system first." Use whatever way works for you.
Let's do an example on the board
(val-rec double (lambda (x) (+ x x)))
What do we know?
Key idea: record the constraint in a typing judgement
a2 = int /\ a2 = int, { double : a1, x : a2 } |- (+ x x) : int
Example: if
(if y 1 0)
y has type 'a3, 1 has type int, 0 has type int
requires what constraint? (int = int, 'a3 = bool)
Example:
(if z z (- 0 z))
z has type 'a3, 0 has type int, - has type int * int -> int
requires what equalities? ('a3 = bool / int = int / 'a3 = int)
is this possible?
why not?
Examples for board:
let val app2 = (lambda (f x y)
(begin
(f x)
(f y)))
let val cc = (lambda (nss) (car (car nss)))
After this lecture, you can write type inference for everything except the let forms. Your type inference can return a type and a constraint.
In place of solve, write a function that prints the constraint to be solved, then returns the identity substitution idsubst.



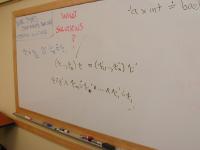
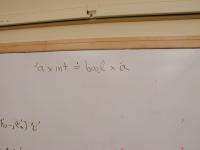
Forall things
managing quantified types
| FORALL contains all variables (because none are free in the context) |
FORALL contains variables not free in the context |
FORALL is empty |
| Generalize over all variables (because none are free in the context) |
Generalize over variables not free in the context |
Never generalize |
Sad news: full type inference for polymorphism is not decidable.
Solution: parameters have monomorphic types
*** Hindley-Milner types ***
datatype ty
= TYCON of name
| CONAPP of ty * ty list
| TYVAR of name
datatype type_scheme
= FORALL of name list * ty
Key ideas:

Key ideas repeated:

{Type inference}:

{Type inference, operationally}:

*** Solve these constraints! ***
datatype con = =*= of ty * ty
| /\ of con * con
| TRIVIAL
infix 4 =*=
infix 3 /\
Q: What constitutes a solution?
A: A standard form (if you missed this class, it's in the book)
Board: which of these have solutions?
'a =*= int
'a =*= int list
'a =*= int -> int
'a =*= 'a
'a =*= tau (arbitrary tau)
Board: which of these have solutions?
int =*= bool
int list =*= bool list
Board: which of these have solutions?
'a * int =*= bool * 'b
'a * int =*= bool -> 'b
Question: in solving tau1 =*= tau2, how many potential cases are there to considerer?
Question: which of these cases are interesting?
Question: how are you going to handle each case?
Now let's see what rules we have applied:
Some constraint-rewriting rules:
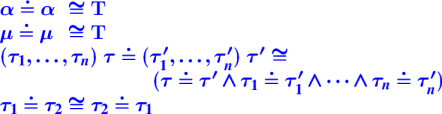
After this lecture, you can write a function which, given a constraint C, has one of three outcomes:
Returns TRIVIAL, in the case where C is trivially satisfied
Calls unsatisfiableEquality in some cases where C cannot be satisfied
Otherwise returns a constraint that is equivalent to C, but in which each simple type equality has a type variable on the left
The last case is the interesting one; on Wednesday we will see how to put such a constraint into standard form, making a complete constraint solver.
Forall things
managing quantified types
| FORALL contains all variables (because none are free in the context) |
FORALL contains variables not free in the context |
FORALL is empty |
| Generalize over all variables (because none are free in the context) |
Generalize over variables not free in the context |
Never generalize |
Examples:
(lambda (ys)
(let ((s (lambda (x) (cons x '()))))
(pair (s 1) (s #t))))
(lambda (ys)
(let ((extend (lambda (x) (cons x ys))))
(pair (extend 1) (extend #t))))
(lambda (ys)
(let ((extend (lambda (x) (cons x ys))))
(extend 1)))
Generalization:
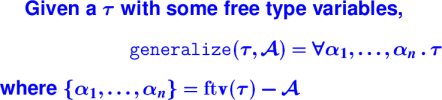
Milner's :

Let with constraints:

Let with constraints, operationally:
typesof: returns tau_1, ..., \tau_n and C_combined
split (C_combined, freetyvarsGamma Gamma) returns C, C-prime
val theta = solve C'
consubst, freetyvarsGamma, union
Map anonymous lambda using generalize, get all the sigma_i
Extend the typing environment Gamma
Recursive call to type checker, gets C_b,
Return (tau, consubst theta C /\ C_b)
Where have we been and where are we going?
Long tour of expressive power at the level of a function or a group of functions. Type systems considered a significant aid to programmers.
A week of foundations: the test bench for new language features
To finish the term, language features designed for larger systems: objects and modules
Only three syntactic forms:
M ::= x | \x.M | M M'
Everything is programming with functions
First example:
(\x.\y.x) M N --> (\y.M) N --> M
Crucial: argument N is never evaluated (could have an infinite loop)
Alert to the reading: Wikipedia is reasonably good on this topic
- EXCEPT for the way they encode lists, which is bogus (violates abstraction)
TA sessions on this topic (when? two days this week)
Everything is continuation-passing style
Q: Who remembers the boolean equation solver?
Q: What classes of results could it produce?
Q: How were the results delivered?
Q: How shall we do Booleans
Booleans take two continuations:
true = \x.\y.x
false = \x.\y.y
if M then N else P = ???
Let's do pairs!
If you have a pair containing a name and a type, how many alternatives are there?
How many continuations?
What information does each expect?
What are the algebraic laws?
Code pair, fst, snd
pair x y k = k x y
fst p = p (\x.\y.x)
snd p = p (\x.\y.y)
How many ways can lists be created?
How many continuations?
What does each continuation expect?
For each creator, what are the laws regarding its continuations?
cons y ys n c = c y ys
nil n c = c
car xs = xs error (\y.\ys.y)
cdr xs = xs error (\y.\ys.ys)
null? xs = xs true (\y.\ys.false)
What do those second continuations look like? (This is the source of Wikipedia's terrible hack)
Board: Wikipedia good: "Church numerals"
Encoding natural numbers:

Church Numerals:
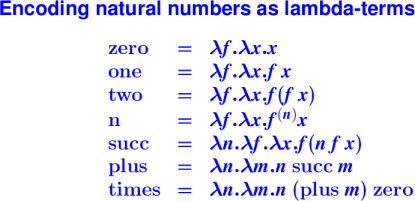
*** Church Numerals to machine integers ***
; uscheme or possibly uhaskell
-> (define to-int (n)
((n ((curry +) 1)) 0))
-> (to-int three)
3
-> (to-int ((times three) four))
12
*** Church Numerals in $\lambda$ ***
zero = \f.\x.x;
succ = \n.\f.\x.f (n f x);
plus = \n.\m.n succ m;
times = \n.\m.n (plus m) zero;
...
-> four;
\f.\x.f (f (f (f x)))
-> three;
\f.\x.f (f (f x))
-> times four three;
\f.\x.f (f (f (f (f (f (f (f (f (f (f (f x)))))))))))
Question: What's missing from this picture?
Answer: We're missing recursive functions.
Astonishing fact: we don't need letrec or val-rec (Friday)
New kind of semantics: small-step
New judgment form
M --> N ("M reduces to N in one step")
No context!! No turnstile!!
Just pushing terms around == calculus
{Reduction rules}:

Board examples:
Are these functions the same?
\x.\y.x
\w.\z.w
Are these functions the same?
\x.\y.z
\w.\z.z
Free variables:
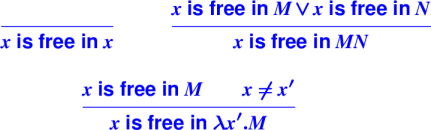
Examples of free variables:
\x . + x y
\x. \y. x
The substitution in the beta rule is the heart of the lambda calculus
- It's hard to get right
- It's a stupid design for real programming (shell, tex, tcl)
- It's even hard for theorists!
- But it's the simplest known thing
Capture-avoiding substitution:
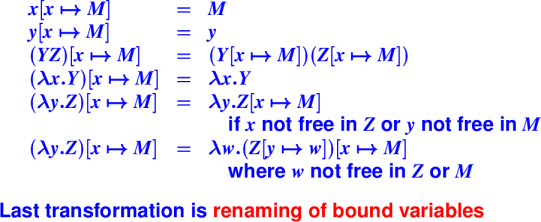
Example:
(\yes.\no.yes)(\time.no) ->
\z.\time.no
and never
\no.\time.no // WRONG!!!!!!
Given a beta-redex
(\x.M) N
do the beta-reduction only if N is in normal form
- Good model for ML and Scheme, so-called "call by value" languages
- Think "arguments before bodies"
Q: Does applicative order ever prevent you from making progress?
A: No. We can prove it by induction on the number of lambdas in N
Normal-order reduction:
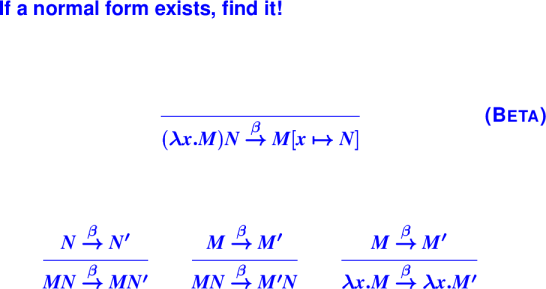
Always choose leftmost, outermost redex
Normalization theorem: if a normal form exists, this will find it
Model for Haskell, Clean
You can try 'uhaskell', but if it does anything useful, we're all surprised and pleased
"Normal-order" stands for produces a normal form, not for "the normal way of doing things"
Normal-order illustration:

Not your typical call-by-value semantics!
What solves this equation?:
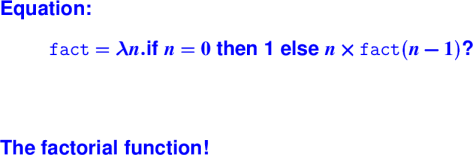
Review:
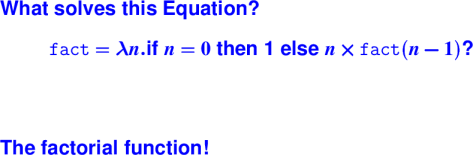
Quiz questions
Is there a solution? Is it unique? If so, what is it?
f1 = \n.\m.(eq? n m) n
(plus n (f1 (succ n) m));
f2 = \n.f2 (isZero? n 100 (pred n));
f3 = \xs.xs nil (\z.\zs.cons 0 (f3 zs));
f4 = \xs.\ys.f4 ys xs;
Wait for it...:

Quiz answers
f1 = \n.\m.(eq? n m) n
(plus n (f1 (succ n) m));
; sigma (sum from n to m)
f2 = \n.f2 (isZero? n 100 (pred n));
; no unique solution (any constant f2)
f3 = \xs.xs nil (\z.\zs.cons 0 (f3 zs));
; map (const 0)
f4 = \xs.\ys. f4 xs ys;
; not unique: constant functions, commutative ops
Recursion = Fixed point:
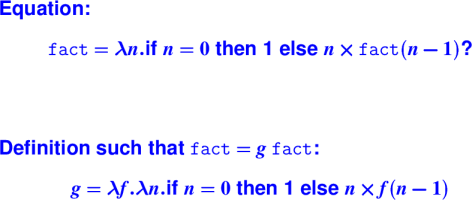
Suppose g F = F. Proof that F is factorial.
For all n, g F n = n!, by induction:
F 0 = g F 0 = 1
F n
= { by assumption }
g F n
= { definition of g }
if n = 0 then 1 else n * F (n-1)
= { assumption, n > 0 }
n * F (n-1)
= { induction hypothesis }
n * (n-1)!
= { definitiion of factorial }
n!
Now you do it
*** Conversion to fixed point ***
length = \xs.null? xs 0 (+ 1 (length (cdr xs)))
lg = \lf.\xs.null? xs 0 (+ 1 (lf (cdr xs)))
One startling idea
You can define a fixed-point operator
A simple algebraic law
If
fix g = g (fix g)
then fix g can define recursive functions!
The only recursion equation you'll ever need
{Y combinator can implement }:
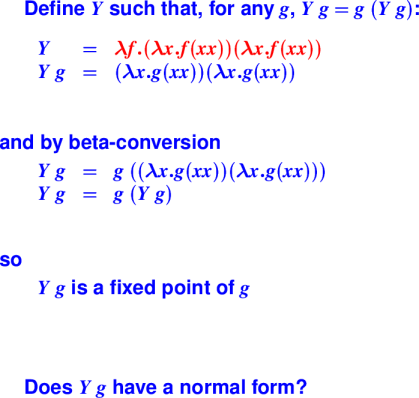
What's its role in the world of theory?
Operational semantics Type theory Denotational Lambda
(Natural deducation style) semantics calculus
-------------------------- ----------- ------------ --------
Interpreters like Python type checkers compilers *models*
Why is it "calculus"?
Differential calculus example: d/dx x^n equals what?
What's going on here?
Answer: pure formal manipulation
No understanding of functions required; you could write a program to do it (and many people have)
What's the role of calculi in computer science:
Lambda calculus:
Process calculus:
Pi calculus:
- Mobile computing and mobile agents
Ambient calculus:
- Security and protection domains
Why so many calculi? They have simple metatheory and proof technique.
Where have we been?
- First code & math
- Then math & code
What kind of code have we been looking at?
- Programming in the small
- Expressive power
Success stories:
- First-class functions
- Algebraic data types and pattern matching
- Polymorphic type systems
What about big programs?
An area of agreement and a great divide:
INFORMATION HIDING
/ \
/ \
reuse / \ modular reasoning
/ \
/ \
OBJECTS MODULES
Two kinds of reuse:
- Inheritance: reuse implementations
- Subtyping: reuse interfaces
Don't conflate them!
We know that mixing code and data can create powerful abstractions (function closures)
Objects are another way to mix code and data
Pioneers were Nygaard and Dahl, who added objects to Algol 60, producing SIMULA-67, the first object-oriented language
Bjarne Stroustrup liked Simula but wanted complete control of costs, so he created C++
James Gosling wanted something a little cleaner and a little more like Simula, created Java
Microsoft funded C#
Objects are everywhere
Agglutination containing
A lot like a closure
Not really useful for building small things
If you build a big, full-featured abstraction, you can easily use inheritance to build another, similar abstraction. Very good at adding new kinds of things that behave similarly to existing things.
Programs that are evolving
A particular kind of evolution: operations stay the same, but we add new kinds of things
For your homework, you'll take a Smalltalk system that has three kinds of numbers, and you'll add a fourth kind of number.
If you do anything at all interesting, your control flow becomes smeared out over half a dozen classes, and your algorithms are nearly impossible to undrstand.
Why Smalltalk?
- Another Turing Award
- Small, simple, pure objects
- Almost the complete language can be done in a relatively small interpreter
Alive and well today
- At the core of Ruby
- As an extension to C ("Objective C") for Apple products
The five questions:
Values are objects (even true, 3, "hello")
Even classes are objects!
There are no functions---only methods on objects
Syntax:
mutable variables
message send
sequential composition of mutations and message sends (side effects)
"blocks" (really closures, objects and closures in one, used as continuations)
No if or while. These are implemented by passing continuations to Boolean objects.
(Smalltalk programmers have been indoctrinated and don't even notice)
Impcore syntax:

Smalltalk syntax:

Smalltalk syntax:

Environments
Types
There is no compile-time type system.
At run time, Smalltalk uses behavioral subtyping, known to Rubyists as "duck typing"
Dynamic semantics
- Main rule is method dispatch (complicated)
- The rest is familiar
The initial basis is enormous
- Why? To demonstrate the benefits of reuse, you need something big enough to reuse.
Look at SEND
- Message identified by name (messages are not values)
- Always sent to a receiver
- Optional arguments must match arity of message name
(no other static checking)
N.B. BLOCK and LITERAL are special objects.
Protocol is Smalltalk term of art:
- The set of messages an object can respond to
- What it is supposed to do on receipt
Ruby dialect "duck typing" is a statement about protocols
Protocol is determined by the class of which an object is an instance
- About classes and instances, more later
SLIDE on Object protocol is not printing :-(

Arities:
- Symbolic messages: arity 1
- Keyword messages: arity is number of colons
Every object gets not just the protocol but the implementations from its class. And a class can inherit from its superclass (more undefined terms) all the way up to class Object.
*** Simple examples ***
-> true
<True>
-> True
<class True>
-> Object
<class Object>
-> (isNil 3)
<False>
-> (isNil nil)
<True>
-> (println nil)
nil
nil
Blocks are closures
Blocks are objects
Booleans use continuation-passing style
Protocol for Booleans:

Booleans implemented with two classes True and False
Classes True and False:

Protocol for Booleans:

Classes True and False:

Board - Method dispatch
To answer a message:
Consider the class of the receiver
Is the method with that name defined?
If so, use it
If not, repeat with the superclass
Run out of superclasses?
"Message not understood"
{ message dispatched to class }:

*** Blocks manage loops ***
-> (val x 10)
-> (val y 20)
-> (whileTrue: [(<= x (* 10 y))]
[(set x (* x 3))])
nil
-> x
270
Protocol for blocks:

Today:
Wide interfaces, reused
Algorithms smeared out over multiple classes
Behavioral subtyping, aka "Duck typing"
Old wine in new bottles
Exceptions
Higher-order methods
Polymorphic methods
Initialization
Double dispatch
Goal of objects is reuse
Key to successful reuse is a well-designed class hierarchy
Killer app: toolkits for building user interfaces
Smalltalk blue book is 90 pages on language, 300 pages on library
Lots of abstract classes
- Define protocols
- Build reusable stuff, just like class
Boolean
``Collection hierarchy'':

|
Collection
|
contain things
|
|
Set
|
objects in no particular order
|
|
KeyedCollection
|
objects accessible by keys
|
|
Dictionary
|
any key
|
|
SequenceableCollection
|
keys are consecutive integers
|
|
List
|
can grow and shrink
|
|
Array
|
fixed size, fast access
|
Collection mutators:

Collection observers:

Collection iterators:

Implementing collections:

Reusable methods:

Question: what's the most efficient way to find the size of a list?
Question: what's the most efficient way to find the size of an array?
{ method}:

Key strategy for reuse in object-oriented languages: subtype polymorphism
A value of the subtype can be used wherever a value of the supertype is expected.
Board:
- SUBTYPE != SUBCLASS
- SUPERTYPE != SUPERCLASS
Only crippled languages like C++ identify subtype with subclass
Only the ignorant and uneducated don't know the difference
Subtyping mathematically:
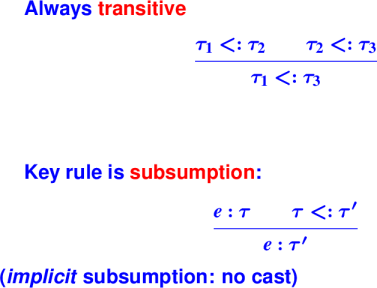
Subtyping is not inheritance:

{The four crucial {} methods}:


Most subclass methods work by delegating all or part of work to list members
N.B. Set is a client of List, not a subclass!
Next example highlight: class method and super!

Typical object-orientation:
- Code you execute depends on class of the receiver
What if you need to choose code based on both receiver and argument?
Solution: method name encodes both operation and type of argument
Examples:
addIntegerTo:
addFloatTo:
Unlocking the final door for building large software systems
You have all gotten good at first-class functions, algebraic data types, and polymorphic types
Modules are the last tool you need to build big systems
Many paths will be open to you:
Direct use of functional programming with modules, largely at hedge funds and investment banks
Board: CUFP 2013, Tuesday 24 September, http://cufp.org
Ideas translate to many other languages
Functions of a true modules system:
Hide representations, implementations, private names
"Firewall" separately compiled units (promote independent compilation)
Possibly reuse units
Real modules include separately compilable interfaces and implementations
Designers almost always choose static type checking, which should be "modular" (i.e., independent)
C and C++ are cheap plastic imitations
- C doesn't provide namespaces
- C++ doesn't provide modular type checking for templates
Collect declarations
- Unlike definition, provides partial information about a name (usually environment and type)
Things typically declared:
Terminology: a module is a client of the interfaces it depends on
Roles of interfaces in programming:
The best-proven technology for structuring large systems.
Means of hiding information (ask "what secret does it hide?")
A contract between programmers
- Essential for large systems
- Parties might be you and your future self
A way to limit what we have to understand about a program
- Estimated force multiplier x10
Interface is the specification or contract that a module implements
- Includes contracts for all declared functions
Two approaches to writing interfaces
Interface "projected" from implementation:
- No separate interface
- Compiler extracts from implementation
(CLU, Java class, Haskell, Oberon)
- When code changes, must extract again
- Few cognitive benefits
Full interfaces:
- Distinct file, separately compiled
(Caml, Java interface, Modula, Ada)
- Implementations can change independently
- Full cognitive benefits
Structure of implementations
Holds all dynamically executed code (expressions/statements)
May include private names
May depend only on interfaces, or on interfaces and implementations both (max cognitive benefits when all dependency is mediated by interfaces)
Dependencies may be implicit or explicit (import, require, use)
The Perl of module languages?
Has all known features
Supports all known styles
Rejoice at the expressive power
Weep at the terminology, the redundancy, the bad design decisions
What we've been using so far is the core language
Modules are a separate language layered on top.
ML module terminology
Interface is a signature
Implementation is a structure
Generic module (parameterized implementation) is a functor
- The point: reuse without violating abstraction
Structures and functors match signatures
Signature says what's in a structure
Specify types (w/kind), values (w/type), exceptions.
Ordinary type examples:
type t // abstract type, kind *
eqtype t
type t = ... // 'manifest' type
datatype t = ...
Type constructors work too
type 'a t // abstract, kind * => *
eqtype 'a t
type 'a t = ...
datatype 'a t = ...
*** Signature example: Integers ***
signature INTEGER = sig
eqtype int (* <-- ABSTRACT type *)
val ~ : int -> int
val + : int * int -> int
val - : int * int -> int
val * : int * int -> int
val div : int * int -> int
val mod : int * int -> int
val > : int * int -> bool
val >= : int * int -> bool
val < : int * int -> bool
val <= : int * int -> bool
val compare : int * int -> order
val toString : int -> string
val fromString : string -> int option
end
Implementations of integers
A selection...
structure Int :> INTEGER
where type int = int
structure Int31 :> INTEGER (* optional *)
structure Int32 :> INTEGER (* optional *)
structure Int64 :> INTEGER (* optional *)
structure IntInf :> INTEGER (* optional *)
What about natural numbers?
signature NATURAL = sig
...
end
And bignums!
functor
BignumFn(Nat:NATURAL) :> INTEGER = ...
Notes:
New course created in 2011
Third time offered
First time things have gone more or less as planned
You know I have high expectations. But your work in March and April has been of high quality and has definitely met those expectations.
First time I have not finished term with a list of terrible things that must be fixed
We clearly have work to do immigrating people into ML. No other big changes in the offing.
Board:
- Improvements (beyond ML)
- Overall ratings
- Experience for all CS majors, or just some?
*** Queues in Standard ML ***
signature QUEUE = sig
type 'a queue (* another abstract type *)
exception Empty
val empty : 'a queue
val put : 'a * 'a queue -> 'a queue
val get : 'a queue -> 'a * 'a queue (* raises Empty *)
(* LAWS: get(put(a, empty)) == (a, empty)
fst(get(put(a, put(a', q)))) == fst(get(put(a', q)))
snd(get(put(a, put(a', q)))) ==
put(a, snd(get(put(a', q))))
*)
end
Error modules, board: Three common implementations (all included on homework)
Your obligations: two types, three functions, algebraic laws
*** Classic ``accumulator'' for errors ***
signature ERROR = sig
type error (* a single error *)
type summary (* summary of what errors occurred *)
val nothing : summary (* no errors *)
val <+> : summary * summary -> summary (* combine *)
val oneError : error -> summary
(* laws: nothing <+> s == s
s <+> nothing == s
s1 <+> (s2 <+> s3) == (s1 <+> s2) <+> s3
// associativity
*)
end
*** Combining generic computations ***
signature COMPUTATION = sig
type 'a comp (* Computation! When run, results in
value of type 'a or error summary *)
val succeeds : 'a -> 'a comp (* a computation
without errors *)
val <$> : ('a -> 'b) * 'a comp -> 'b comp
(* apply a pure function to a computation *)
val <*> : ('a -> 'b) comp * 'a comp -> 'b comp
(* application inside computations *)
val >>= : 'a comp * ('a -> 'b comp) -> 'b comp
(* computation followed by continuation *)
end
*** {Buckets of \emph{generic} algebraic laws} ***
succeeds x >>= k == k a // identity
comp >>= succeeds == comp // identity
comp >>= (fn x => k x >>= h) == (comp >>= k) >>= h
// associativity
// compare comp >>= (fn x => comp') with
// "let x = comp in comp'"
// (fn x => comp') comp
f <$> c == succeeds f <*> c
(fn x => x) <$> c == c // identity
curry (op o) <$> u <*> v <*> w == u <*> (v <*> w)
// compare: curry (op o) u' v' w' = u' (v' w')
succeeds f <*> succeeds x == succeeds (f x) // success
*** Variation on environments ***
signature COMPENV = sig
type 'a env (* environment mapping strings
to values of type 'a *)
type 'a comp (* computation of 'a or
an error summary *)
val lookup : string * 'a env -> 'a comp
end
*** Payoff! ***
functor InterpFn(structure Error : ERROR
structure Comp : COMPUTATION
structure Env : COMPENV
val zerodivide : Error.error
val error : Error.error -> 'a Comp.comp
(* LOOK --> *) sharing type Comp.comp = Env.comp) =
struct
fun curry f x y = f (x, y)
val (<*>, <$>, >>=) = (Comp.<*>, Comp.<$>, Comp.>>=)
infix 4 <$>
infix 3 <*> >>=
...
end
*** SLIDE ***
datatype exp = LIT of int
| VAR of string
| PLUS of exp * exp
| DIV of exp * exp
fun eval (e, rho) =
let fun ev(LIT n) = Comp.succeeds n
| ev(VAR x) = Env.lookup (x, rho)
| ev(PLUS (e1, e2)) = curry op + <$> ev e1 <*> ev e2
| ev(DIV (e1, e2)) = ev e1 >>= (fn n1 =>
ev e2 >>= (fn n2 =>
case n2
of 0 => error zerodivide
| _ => Comp.succeeds
(n1 div n2)))
in ev e
end
Board:
eval e1 + eval e2
op + (eval e1, eval e2)
curry op + (eval e1) (eval e2)
curry op + <$> ev e1 <*> ev e2
Homework review:
- Basic data structure, what do you need to know to implement it?
- Three implementations of error summaries
- Heapsort without a heap
- Implementing a large interface: the tic-tac-toe game. Choose a representation; write lots of sturdy little functions.
- The abstract game solver. A search problem. Not your first. Keep it simple!
Reading:
What's going on in this example:
Lots of interfaces using ML signatures
An idea how to compose large systems
Use case for the error summaries in homework, part 2 (coming)
Some ambitious, very abstract abstractions---it's the last week of class, and you should see something ambitious.
Practice implementing functors
*** ``Accumulator'' has many implementations ***
signature ERROR = sig type error (* a single error ) type summary ( summary of what errors occurred *)
val nothing : summary (* no errors *) val <+> : summary * summary -> summary (* combine *)
val oneError : error -> summary
(* laws: nothing <+> s == s s <+> nothing == s s1 <+> (s2 <+> s3) == (s1 <+> s2) <+> s3
// associativity *) end
Computations are the big ambitious thing.
We're doing errors, but these can include:
Errors
Probability
I/O
Search
Database access
*** Review: Generic computations ***
signature COMPUTATION = sig type 'a comp (* Computation! When run, results in value of type 'a or error summary *)
val succeeds : 'a -> 'a comp (* a computation without errors *)
val <$> : ('a -> 'b) * 'a comp -> 'b comp (* apply a pure function to a computation ) val <> : ('a -> 'b) comp * 'a comp -> 'b comp (* application inside computations *)
val >>= : 'a comp * ('a -> 'b comp) -> 'b comp (* computation followed by continuation *) end
*** Environments using ``computation'' ***
signature COMPENV = sig type 'a env (* environment mapping strings to values of type 'a ) type 'a comp ( computation of 'a or an error summary *)
val lookup : string * 'a env -> 'a comp end
*** Build an interpreter ***
functor InterpFn(structure Error : ERROR structure Comp : COMPUTATION structure Env : COMPENV val zerodivide : Error.error val error : Error.error -> 'a Comp.comp (* LOOK --> *) sharing type Comp.comp = Env.comp) = struct fun curry f x y = f (x, y)
val (<>, < > , > > = ) = (Comp. < * > , Comp. < >, Comp.>>=) infix 4 <$> infix 3 <> >>= ... end
*** SLIDE ***
datatype exp = LIT of int | VAR of string | PLUS of exp * exp | DIV of exp * exp
fun eval (e, rho) = let fun ev(LIT n) = Comp.succeeds n | ev(VAR x) = Env.lookup (x, rho) | ev(PLUS (e1, e2)) = curry op + <$> ev e1 <*> ev e2 | ev(DIV (e1, e2)) = ev e1 >>= (fn n1 => ev e2 >>= (fn n2 => case n2 of 0 => error zerodivide | _ => Comp.succeeds (n1 div n2))) in ev e end
*** Homework, problem 2 ***
signature ERROR = sig type error (* a single error ) type summary ( summary of what errors occurred *)
val nothing : summary (* no errors *) val <+> : summary * summary -> summary (* combine *)
val oneError : error -> summary
(* laws: nothing <+> s == s s <+> nothing == s s1 <+> (s2 <+> s3) == (s1 <+> s2) <+> s3
// associativity *) end
*** {Extend a signature with \lit{include}} ***
signature ERRORCOMP = sig include COMPUTATION structure Error : ERROR (* <-- LOOK ) datatype 'a result = SUCC of 'a | ERR of Error.summary val run : 'a comp -> 'a result ( <-- LOOK *) val error : Error.error -> 'a comp end
*** {Let's build \lit{ERRORCOMP}} ***
functor ErrorCompFn(structure Error : ERROR) :> ERRORCOMP where type Error.error = Error.error and type Error.summary = Error.summary = struct structure Error = Error datatype 'a result = SUCC of 'a | ERR of Error.summary
type 'a comp = 'a result fun run comp = comp
... succeeds ... ... error ...
*** {Computation combinators for \lit{ERRORCOMP}} ***
infix 4 <$> infix 3 <*> >>=
fun ... <*> ... = ...
fun f <$> c = ...
fun ... >>= ... = ...
end
Solutions:
fun (SUCC f) <*> (SUCC x) = SUCC (f x) (* success law *)
| (SUCC f) <*> (ERR s ) = ERR s
| (ERR s) <*> (SUCC x) = ERR s
| (ERR s) <*> (ERR s') = ERR (Error.<+> (s, s'))
fun f <$> c = succeeds f <*> c
fun (SUCC a) >>= k = k a
| (ERR s) >>= _ = ERR s
1970s: What is logic programming?
How does logic programming (Prolog) fit in with the functional and imperative programming we know?
Prolog is backtracking search plus constraint solving. It's used to create derivations (syntactic proofs). The key idea is that you can give Prolog a judgment form in which certain parts are "left blank" as metavariables or "logical variables". The search algorithm fills these in. So for example you can present a judgement containing a term and a context and ask for all types the term can have in that context.
Can you just briefly mention what Denotational Semantics is? The fact that we didn't cover it makes me want to know now.
Denotational semantics combines two ideas:
We call certain code "functions." Do they have anything to do with real functions? Does a program stand for anything besides itself?
Dana Scott says yes: a program stands for a monotonic, continuous function.
A program is made of syntax, and syntax is formed from other syntax. Christopher Strachey showed that we could compute the meaning of a program by associating each syntactic combining form with a semantic equation, which tells us what the syntax means by combining the meanings of the syntax of its parts. This technique is much easier than it sounds, and it is the basis for all modern compilers (as well as many other program analyses).
1980s onward: What are the descendants of Smalltalk?
If we prefer Smalltalk to the other languages covered in class, what would be the best modern language/area to pursue?
Ruby, hands down.
You might also want to read Self: The Power of Simplicity by David Ungar, then try some JavaScript.
2010s: How is functional programming used today?
I'd like to hear about some of the applications of functional programming in industry/academia.
In industry, primarily banks, hedge funds, and startups. Also a huge chunk of Ericsson's telecoms structure (phone switches and cellphone towers). Web payments in Sweden. And a dairy processor in New Zealand.
Also see http://cufp.org, the Commercial Uses series in the Journal of Functional Programming, and Google the term "ICFP Experience Report."
In academia, any problem to do with program analysis and compilation. Many problems to do with parallelism. This includes, for example, running general-purpose codes on GPUs.
How have designers of scripting languages like Python have blended functional, imperative, and object-oriented -ideologies- paradigms?
Guido has done it badly, like a magpie: toss in any feature that looks good.
Roberto and Luiz have done it well: draw from many sources of inspiration, but take a very small amount from each one and craft the pieces together into a unified design.
Go study Lua.
I want to hear the Norman Ramsey story! How you got into programming, what different jobs and projects you've worked on, ...
That's a conversation for the Tower Cafe where we can spend the deans' money on delicious drinks...
Back to class home page