Due Tuesday, January 31, 2017 at 11:59PM.
This first assignment is divided into three parts:
Comprehension questions that help you focus your reading
Programming exercises that reinforce your skills with induction and recursion
A photograph for the private use of the course staff, which will help us learn to recognize you and call you by name
NOTE: This assignment is due one minute before midnight. You may turn it in up to 24 hours after the due date, which will cost you one extension token. If you wish not to spend an extension token, then when midnight arrives submit whatever you have. We are very willing to give partial credit.
ALERT: This assignment is three or four times easier than a typical COMP 105 assignment. Its role is to get you acclimated and to help you start thinking systematically about how recursion works. Later assignments get much harder and more time-consuming, so don’t use this one to gauge the difficulty of the course.
Reading-Comprehension Questions (10%)
Please read pages 6–13 and 15 in the book by Ramsey. Then place the answers to the following questions in a text file called cqs.impcore.txt:
What is the value of the following Impcore expression?
(if (> 3 5) 17 99)Which of the following best describes the syntactic structure of Impcore?
- An expression can contain a definition
- A definition can contain an expression
- Both of the above
- None of the above
What is the value of the following Impcore expression:
(while (> n 0) (begin (set n (- n 1)) 33))Does this Impcore test pass? Why or why not?
(check-expect (+ 1 2 3) 6)Does this Impcore test pass? Why or why not?
(check-error (+ 1 2 3))
Next read about abstract syntax on pages 16 and 17.
After reading about abstract syntax, look at this picture of an abstract-syntax tree for a “calculator expression”:
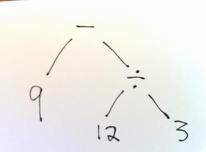
Answer these questions:
- What concrete syntax could you write in C for this expression?
- What concrete syntax could you write in Impcore for this expression?
- How many different concrete C expressions describe the same computation?
- How many different concrete Impcore expressions describe the same computation?
Note: the “computation” is the act of dividing 12 by 3, then subtracting the result from 9. It’s a different computation from, say, adding 2 and 3, which although it produces the same value, is not the same computation.
You can download the questions.
Programming in Impcore (80%)
The problems below are simple programming exercises that serve multiple purposes: to get you thinking explicitly about induction and recursion, to get you acclimated to the LISP-style concrete syntax used throughout the course, to get you started with the course software, and to help you practice the forms of testing and documentation that are expected in the course. You can start these exercises immediately after the first lecture. If you find it entertaining, you may write very efficient solutions—but do not feel compelled to do so.
Do not share your solutions with anyone. We encourage you to discuss ideas, but noone else may see your code.
Getting set up with the software
The interpreter you need to run Impcore code is provided as part of the course. To add course software to your execution path, run
use -q comp105You may want to put this command in your .cshrc or your .profile. The -q option is needed to prevent use from spraying text onto standard output, which may interfere with with scp, ssh, git, and rsync.
The impcore interpreter is in /comp/105/bin; if you have run use as suggested above you should be able to run it just by typing
ledit impcoreThe ledit command gives you the ability to retrieve and edit previous lines of input.
If your code and unit tests are in file solution.imp, you can load and run them by typing
impcore -q < solution.impUnit testing
The special “extended-definition forms” check-expect and check-error are part of every language in the book. For example, as described in Section 1.1 of the book, they are part of the Impcore language. These forms serve both as unit tests and as documentation. Every function you write must be tested and documented using check-expect, and possibly also check-error. The number of unit tests must be appropriate to the function’s contract and to the structure of its input. In this first assignment, you should briefly explain the purpose of each check-expect definition, and you should explain why those check-expects are necessary and sufficient to test the code.
Documentation
In addition to its unit tests, each function should be documented by a contract which explains what the function does. Here’s an example:
;; (occurs-in? d n) returns 1 if and only if decimal digit `d`
;; occurs in the decimal representation of the positive integer
;; `n`; it returns 0 otherwise.The coding guidelines explain contracts at length; read them. The contract is typically supplemented by unit tests, which can serve to clarify the contract:
(check-expect (occurs-in? 7 123) 0)
(check-expect (occurs-in? 2 123) 1)For this assignment, I am also asking you to explain your inductive reasoning. Below each function, not as part of that function’s regular documentation, please put a comment that explains what inductive structure that function is imposing on the integers or the natural numbers. For example, I could write the even? function this way:
;; (even? n) is given a natural number n; it returns 1 if n is
;; even and 0 otherwise
;;
(define even? (n)
(if (= n 0) 1
(if (= n 1) 0
(even? (- n 2)))))
;; Breaks down the natural numbers into three cases:
;; 0
;; 1
;; n+2, where n is a natural numberA jumping-off point for your solution
You will put your solutions in a file solution.imp, and you will write up your whole assignment in a README file. At http://www.cs.tufts.edu/comp/105/homework/solution_template.imp and http://www.cs.tufts.edu/comp/105/homework/README_template, we provide templates for solution.imp and README.
To turn the solution template into a real solution, follow these steps for each function:
In a comment, you will find a template for the function’s contract. Edit the contract to make it specific and accurate. Use the coding guidelines.
You will find one unit test that uses
check-error. The test is a placeholder. Remove thecheck-errorand replace it withcheck-expectunit tests, which you will write yourself. (You will need multiple unit tests: at least one per base case and per induction step.)You will find a function definition with the body
(/ 1 0). Evaluating this code divides 1 by 0, which causes an error. Replace this code with your implementation of the function.Below the function definition you will find a block comment containing a placeholder for your analysis of the induction in the function. Replace the placeholder with your actual analysis.
If you write any helper functions, supply each helper function with a contract and with unit tests.
The problems you must solve
Do Exercises 4, 5, 7, 8, and 10 on pages 71–74 of Ramsey’s textbook. Also do problem DD below.
DD. Function double-digit accepts a positive integer less than 20,000, and it returns a positive integer whose decimal representation is the same as the decimal representation of the input, except each digit appears twice. For example, (double-digit 123) is 112233. Implement double-digit.
These problems stress induction and recursion, which is the topic of the first class. And your recitation will address these kinds of problems. But a couple of them may still be challenging; if you have difficulty, consult a member of the course staff or ask questions on Piazza.
My solutions total 50–60 lines of Impcore.
Expectations for your solutions
This assignment lays the foundations for much that is to come. Here’s what we expect:
Your solutions must be valid Impcore; in particular, they must pass the following test:
/comp/105/bin/impcore -q < solution.imp > /dev/nullwith no error messages and no unit-test failures. If your file produces error messages, we won’t test your solution and you will earn No Credit for functional correctness (you can still earn credit for readability).
Your solutions must load and complete within 250 CPU milliseconds. If you write any long-running test, don’t include them in
solution.imp; instead, create a fileextra-tests.imp.On this assignment, as on several assignments to come, you must use recursion. Code using
whileloops will receive No Credit.You may use helper functions where appropriate, but you must not use global variables.
Your code must be your own work. Do not share your solutions with anyone. We encourage you to discuss ideas, but no one else may see your code.
A photograph we can use to learn your name (10%)
I hope to learn the name of every student in the class. The teaching assistants and recitation leaders would also like to learn your name. But we need your help. Part of the assignment, for 10% of the grade on the assignment, is to submit a photograph that will help us learn to recognize you. I’ve consulted with a skilled portrait photographer to prepare guidelines for producing a good, easily recognizable photograph, even if all you have is a cellphone camera. You’ll submit the photo as photo.jpg.
What to submit and how to submit it
You’ll choose a directory for your assignment, in which you will create or copy these files:
cqs.impcore.txtwill contain the comprehension questions and your answerssolution.impwill contain your code, with its documentation and unit tests. Problems will appear in order by number, with problem DD last.photo.jpgwill contain a recognizable photograph of you.READMEwillGive your name and explain how to pronounce it, as in “kaeth-lEEn FI-shur” or “NORE-muhn RAM-zee.”
Identify anyone with whom you have collaborated or discussed the assignment
Say approximately how many hours you have spent completing the assignment.
As soon as you have the files listed above, run submit105-impcore to submit a preliminary version of your work. Keep submitting until your work is complete; we grade only the last submission.
You may also submit extra-tests.imp, which should contain only test code and unit tests (check-expect or check-error). You can run the tests using the Unix command
cat solution.imp extra-tests.imp | impcore -qHow your work will be evaluated
How your code will be evaluated
A big part of this assignment is for you to be sure you understand how we expect your code to be structured and organized. There is some material about this on the coding style page on the course web site. When we get your work, we will evaluate it in two ways:
About 50% of your grade for the assignment will be based on our judgement of the structure and organization of your code. To judge structure and organization, we will use the following dimensions:
Documentation assesses whether your code is documented appropriately.
We expect you to document each function such that someone else could use your code and reason about its result without having to see the code itself. In particular, every function must be documented with a contract, and the contract must mention each parameter by name.
For this assignment, we also expect you to document your analysis of the inductive struture used by each function. Your analysis should explicitly identify which cases are base cases and which are inductive steps.
And remember that every named parameter should be mentioned in a function’s contract.
Unit testing assesses whether your code is appropriately tested by
check-expectand/orcheck-error.We expect that you will write enough unit tests to test every part of your code. And we expect a unit test for every base case and induction step in your analysis of the inductive structure of numbers.
Form assesses whether your code uses indentation, line breaks, and comments in a way that makes it easy for us to read.
We expect you to use consistent indentation, to obey the offside rule described in the coding-style guidelines, and to limit the use of inline comments in the body of each function.
Naming assesses your choice of names. To people who aspire to be great programmers, names matter deeply.
We give you a hand here by providing a template in which the names of top-level functions and their arguments are already chosen for you. For helper functions, you will choose your own names. Look at the coding rubric and choose wisely.
Structure assesses the underlying structure of your solution, not just how its elements are documented, formatted, and named.
We expect that if asked to use recursion, your solution will use recursion. Additionally, we expect that your recursive structure will be minimal, avoiding superfluous cases—especially redundant base cases—and unnecessary comparisons.
About 30% of your grade for the assignment will be based on our judgement of the correctness of your code. We often look at code to see if it is correct, but our primary tool for assessing correctness is by testing. On a typical assignment, the correctness of your code would carry more weight, but relative to the other homeworks in 105, the problems on this assignment are very easy, so they carry less weight.
The detailed criteria we will use to assess your code are found at http://www.cs.tufts.edu/comp/105/coding-rubric.html. Though things may be worded differently, most of these criteria are also applied in COMP 11, 15, and 40—they make explicit what we mean by “good programming practice.” But as you might imagine, there is a lot of information there—probably more than you can assimilate in one reading. The highlights are
- Documentation
- Each function is documented with a contract that explains what the function returns, in terms of the parameters, which are mentioned by name. From documentation, it is easy to determine how each parameter affects the result.
- The contract makes it possible to use the function without looking at the code in the body.
- Documentation appears consistent with the code being described.
- Each parameter is mentioned in the documentation at least once.
- In every case analysis, all cases are necessary.
- Unit Testing
- Unit tests cover the branches of execution for the function.
- Unit tests test input which is valid per the problem definition.
- Form
- Code fits in 80 columns.
- Code respects the offside rule.
- Code contains no tab characters.
- Indentation is consistent everywhere.
- If a construct spans multiple lines, its closing parenthesis appears at the end of a line, possibly grouped with one or more other closing parentheses—never on a line by itself.
- No code is commented out.
- Solutions load and run without calling
print
- Naming
- Each function is named either with a noun describing the result it returns, or with a verb describing the action it does to its argument. (Or the function is a predicate and is named as suggested below.)
- A function that is used as a predicate (for if or while) has a name that is formed by writing a property followed by a question mark. Examples might include even? or prime?. (Applies only if the language permits question marks in names.)
- In a function definition, the name of each parameter is a noun saying what, in the world of ideas, the parameter represents.
- Or the name of a parameter is the name of an entity in the problem statement, or a name from the underlying mathematics.
- Or the name of a parameter is short and conventional. For example, a magnitude or count might be n or m. An index might be i, j, or k. A pointer might be p; a string might be s. A variable might be x; an expression might be e.
- Structure
- Solutions are recursive, as requested in the assignment.
- There’s only as much code as is needed to do the job.
- In the body of a recursive function, the code that handles the base case(s) appears before any recursive calls.
- The code of each function is so clear that, with the help of the function’s contract, course staff can easily tell whether the code is correct or incorrect.
- Expressions cannot be made any simpler by application of algebraic laws.
- Solutions are recursive, as requested in the assignment.
How your photograph will be evaluated
If your photograph is clear, makes it easy to recognize you, and is not ridiculous in size, it will earn a grade of Very Good (the top grade). If you’re not sure how to take a photograph that makes you easy to recognize, I consulted with a skilled portrait photographer for some tips. In the table below, you want to aim for “Exemplary” (the left column), be willing to settle for “Satisfactory” (the middle column), and avoid “Must Improve” (the right column).1
| Exemplary | Satisfactory | Must improve | |
|---|---|---|---|
| Composition |
• Head and shoulders fill 2/3 to 3/4 of the frame. • The shot is taken from a distance of 4 to 6 feet, and the camera is zoomed as needed to include just head and shoulders. • Or, the shot is taken from a distance of 4 to 6 feet, then cropped to include just head and shoulders. • The subject is looking at the camera with a normal look on the face. |
• Face fills the frame; shoulders not visible. • The subject is not looking at the camera, but there is a normal look on the face. |
• Photo down to waist; full-body photo. • More than one person visible in photo. • Eyes are closed. • The camera is too close to the subject. (This will happen if you compose the shot by moving the camera toward the subject until the subject’s head and shoulders fill the “viewfinder”; you’ll get perspective distortion.) • The subject is making a strange face (eye rolls, etc) |
| Lighting |
• The subject is illuminated by two or more light sources, such that one side of the subject’s face is noticeably brighter than the other (about 2 to 1). • The main sources of light are soft and diffuse: overcast sky, indirect daylight, daylight reflected off a wall or building, and so on. |
• The subject’s face is lit evenly. • The subject’s face is lit by ambient light, plus flash bounced off a ceiling or wall (possible only with a real camera) |
• The background is significantly brighter than the subject. • There is light behind the subject aimed at the camera. • The sun is shining in the subject’s face. • The subject is illuminated by a camera flash. |
| Focus |
• The subject is in sharp focus, while the background is a little blurry (possibly only with a real camera or with very sophisticated software). • The subject’s face is in sharp focus. |
• Some part of the subject is in sharp focus, or something near the subject is in sharp focus. The subject’s face is not in sharp focus but is still easy to recognize. |
• The subject’s face is out of focus. |
| File |
• The uploaded image file is from 300KB to 1.2MB in size. • Resolution of the uploaded file is high enough that there’s no pixelation. • The uploaded image is at least as tall as it is wide (portrait orientation) |
• The uploaded image file is at most 2MB in size. • When shown at a few inches high, the uploaded image file is pixelated or has compression blur. |
• The uploaded image file is more than 2MB in size. • At its natural resolution, the uploaded image file shows pixels or compression artifacts. • The uploaded image is wider than it is tall (landscape orientation) |