
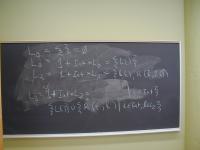
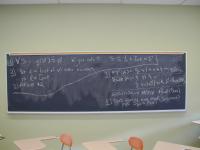
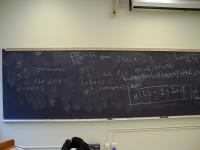
An unusual kind of course; I haven't done something like this in five or six years.
Spectrum of courses:
Long-established knowledge that every educated computer scientist should know. Found in textbooks. Taught in required courses.
Established knowledge that many working computer scientists might wish to know. Found in textbooks. Taught as elective courses, but available every year.
Recently discovered knowledge. Found in research papers but not in textbooks. Often taught as special topics (150) or some other numbering suitable for graduate students. This kind of course comes in at least two flavors:
Create new knowledge. Builds on existing knowledge, but by definition, is not found everywhere.
I set up this course with the goal of creating new knowledge about dataflow analysis and optimization.
Especially good for the PhD students—should lead to papers, which is their lifeblood.
Fun for everyone.
Not a requirement: it will be sufficient for you to learn something that is not in the regular curriculum.
Problem: new knowledge builds on existing knowledge
(You have to get to the frontier before you can extend it.)
By and large, the existing knowledge is not in our curriculum.
And all of you come with different knowledge in your heads.
So the plan is something like this:
Get everybody up to speed. I'm hoping this can be done in four weeks.
Spend the rest of the term on projects.
Each of you can pick your own projects; John and I are here to help you pick good ones. And you can work in teams of any size. At the end of the term you'll give a juried presentation and about a week later you'll turn in a paper.
What I hope to accomplish today:
Talk about logistics
Explain what our obligations are and how this class is different from other classes you may have taken
Tell you why I thought this would be a very cool topic for an exploratory course
Teach a little bit of material
I imagine the course is going to proceed in three phases:
Phase One: Established knowledge. This is getting everybody up to speed on the problem, the foundations, the interesting bits of compilers, and the implementation technology we'll use. Phase One will be based on lectures and exercises. We'll do some exercises in class, but I'll also ask you do so some at home, then bring the results in for Show and Tell.
Phase Two: Paper discussions. There are at least a handful of absolutely critical papers we have to understand to move forward. If everyone here were a graduate student, I would insist on the "learn to grapple with papers yourself" method. But since we have a mix, I'll try to get the sense of what you want to do and what we think would be most effective.
Even if you're not purusing a PhD, it's still incredibly useful to be able to read research papers---it's the royal road to learning new technologies and to making yourself more knowledgable and more valuable to the people around you.
Phase Three: Projects. Once everyone is up to speed, all our resources will be dedicated to helping you with your projects.
Phases Two and Three are the reason this class has a special exemption from the registrar to run for four hours per week instead of two and half—75&minutes simply isn't enough time to grapple with a research paper or present and discuss a problem you are working on. In Phase One I hope to give an hour of lecture and then follow up with an hour of in-class exercises.
A seminar: collaborative and participatory
If you've heard about my undergrad course, you may have heard about these properties:
150DFO is a dramatically different course. We will still work on challenging problems, but everything else is different:
Focus is on problems you pick (within broad parameters)
Secondary focus on reading, understanding, and evaluating
Almost no advance script. Instead, . A goal . Teaching that is custom tailored to get each of you from where you are to the starting gate . A native guide through the jungle of unsolved problems
Pace will be less relentless
In 40, it's already decided what you need to learn, and you
learn most of it outside class by doing projects.
The role of class time is mostly to prepare you to do this work.
(Some of the starting-gate stuff in 150DFO may have this flavor.)
In 150DFO, you will have some choices about what you want to learn:
I hope many of you will choose to learn new things: answers to questions whose answers are not yet known.
You will all also have the choice of selecting some advanced topic where answers are known, but you pick the topic you want to learn about.
Once we are all at the starting gate, I intend that most of our class time will be spent in sharing and organizing knowledge acquired outside of class. Rather than simply have some instructor decide, you will work hard to synthesize a coherent picture of what you want to know.
Class succeeds to the extent that everyone is prepared and energized.
Therefore, if you're not on board and active, the entire outcome of the course is changed---everyone loses. This is the single biggest difference from a typical lecture-and-project course like 40.
If you decide to take the course, you have a moral obligation to be a full part of the group, not just a passive observer. (We all work to create what's going on here, and to sit and take would be almost stealing.)
One way to view what is going on: we have a semester-long conversation that leads us to consensus on:
So why do things this way? Two reasons:
What is my role?
None of the starting-gate exercises count toward a final grade. You will be getting plenty of formative evaluation but little summative evaluation. (A formative evaluation tells you how to make your work better; a summative evaluation tells you how good your work is right now.)
Essentially all your grade is based on the answer to this question: have you made a good-faith effort to bring off a quality project? This kind of effort requires a lot of ingredients:
Have you worked diligently to get youself to the starting gate?
Have you been a good colleague with whom to discuss papers?
Have you been a colleague with whom to work on projects?
Are you bringing exciting work for the group to hear about? (Anything counts as exciting work as long as you are genuinely excited about it.)
Are you listening carefully to other people's work and helping them to improve?
Can you make a presentation that will impress a jury of talented people from outside Tufts?
Have you written up your work for the archival record, so that you show clearly what you have learned, and so others may be able to build on your work?
I suspect some of this sounds intimidating. Let me assure you it is way more fun than writing problem sets and exams. We've got a huge playground, and you're invited to find whatever you like best on the playground and do something interesting with it.
Preface: why I hated this subject in school
The "optimization zoo"
An endless supply of analyses
Arcane algorithms and notation
But languages people like things to be compositional, and there is another view:
We hope for code-improving transformations (aka "optimizations").
We must have semantics-preserving transformations, also called sound transformations.
Claim: there are really only two transformations:
Remove an assignment whose result is not used (example)
Substitute equals for equals
These transformations compose to make all the classical optimizations!
These transformations are justified by logic.
Observation: these transformations are local.
Note: there is a third kind of transformation, which is not local: a change of representation (e.g., lambda lifting, closure conversion, unboxing). These kinds of transformations are very important for functional languages and for very dynamic object-oriented languages like Self. They are more or less forbideen in C and C++, and they are unlikely in Java.
The key assumption underlying this line of work (and therefore this course) is that
Although the "optimization zoo" in the Dragon book is ugly, we believe we see connections to the semantics of programmings languages and to the logic of programs, which is beautiful.
So far, while semanticists have been thinking beautiful thoughts, compiler writers have been writing ugly code. Our goal is twofold:
Create beautiful code that reflects the beautiful thoughts, which can nevertheless be used to write optimizing compilers.
Change the way compiler writers think about their craft.
Can we really make it easy to implement optimizations? Advanced onces?
What optimizations combine well?
How to ensure soundness?
Is our stuff really better than existing stuff?
Build a compiler to try out ideas
Play around with the Glasgow Haskell Compiler (optimization and code generation)?
Explore whole-program optimization for a language like Lua or Javascript.
How do you test an optimization?
How do you test an optimization library?
Hear from each student. Tell us
All a dataflow analysis does is solve recursion equations. But they are useful recursion equations because the solutions tell you facts about your program. We're going to start with something simpler: recursion equations for defining data types. Here's the plan:
Same methods everywhere!
What is a list of integers? How about a solution to this equation?
List(Int) = 1 + Int * List(Int)
Or informally
A list of integers is either empty or it is an integer followed by a list of integers Perhaps surprisingly, this equation does not have a unique solution!
Notation:
1 -- the unit type, which has exactly one element
-- for this exercise we'll pronounce the element "nil"
A + B -- either an A or a B, and it's tagged whether the thing
-- came from the left or the right
Example
Bool = 1 + 1
More notation
A * B = { (x, y) | x in A, y in B }
I'll show you how to construct the solution used in most programming languages:
L0 = { } -- the empty set
L1 = 1 + Int * L0
L2 = 1 + Int * L1
...
Ln = 1 + Int * L_{n-1}
Now let L = union over n>=0 of L_n.
I claim
Lsolves the recursion equation forList(Int)
Exercise: prove it (right now)
Notice something:
Ln = f (Ln - 1)
where
f = \ S . 1 + Int * S
(who has or has not seen lambda?)
Notice that f has no recursion in it; f is a perfectly well
defined mathematical function. (Dana Scott nailed this down in the
1970s.)
I claim that if a set H has the property that f(H) == H, then H
is a solution to the recursion equation for list of integers.
Exercise: prove it (right now)
Actually I claim this is "if and only if"
Exercise: prove it (right now)
Notice
L0 = { }
L1 = f(L0)
L2 = f(f(L0))
L3 = f(f(f(L0)))
and so on!
L = union over n>=0 of L_n
Question: is the list of all even numbers a member of L?
Exercise: prove your answer!
The technique just shown is constructive, and it computes the least fixed point of a function. To have a least fixed point, the function must be
For set-theoretic functions, the least element is the empty set.
The least fixed point is the smallest solution to the equations, and it contains all the others.
What's "constructive"?
Consider the powerset construction: P(A) is the set of all subset of A. Assuming that given a set, we can enumerate its elements but not its subsets, the following definition is not constructive:
Power(A) = { S | S subset A }
Let's make it constructive by looping only over elements:
Power(A) = { { } } union { {x} union S | x in A, S in Power(A) }
Exercise: Compute Power(Bool)
Exercise:
Considering this equation:
PB = { { } } union { {x} union S | x in Bool, S in PB }
does it have any solutions other than
Power(Bool)?
I have written a handout on the refinement ordering and fixed points.
Problems from last time:
Show that forall S : g(S) = S if and only ifS = 1 + Int * S`.
Show the same for isomorphism.
(Proof technique for implying an equality or other relation: Assume the left-hand side as hypothesis, then use calculation to show the relation.)
Example: show that if g(S) = S, then = S = 1 + Int * S:
S
= [by hypothesis]
g(S)
= [by definition of `g`]
1 + Int * S
The opposite direction is similar.
Let e be the list of all even numbers. Is e in Lint, where
Lint = union over n >=0 of L_n?
No.
Simplest proof: for all
n, every element ofL_nis finite.By the axiom of choice if
l in Lint, the there exists annsuch thatl in L_n. Thereforelis finite.Because
eis not finite, it can't be inL_n
Consider this recursion equation for power sets of A:
Power(A) = { {} } union { {x} union S | x in A, S in Power(A) }
Construct the least solution for Power(Bool) using the
technique of sequential approximation from class.
Does equation 4 have other solutions for Power(Bool)?
Solution: start fixed-point construction with the set {yellow}:
Y0 = { yellow }
Y1 = { {}, {true, yellow}, {false, yellow} }
Y2 = { {}, {true}, {true, yellow} , {true, false, yellow},
{false}, {false, yellow} }
Y3 = { {}, {true}, {true, yellow} , {true, false, yellow},
{false}, {false, yellow}, {true, false} }
Y4 = Y3
So far we have zero, one, cross (times), plus, and primitive sets like Int and Bool. This mathetmatics is analogous to what Richard Bird calls "wholemeal programming"---dealing with big values. Functinoal programmers like it.
We also have explicit set constructions using set comprehensions and
the element-of or in operator. This mathematics is analogous to
writing recursive functions that poke at data structures.
Now let's make this analogy more explicit.
Never mind what it means; let's look at syntax.
Math:
Lint = 1 + Int * Lint
Standard ML:
datatype lint = Nil | Cons of int * lint
Haskell:
data Lint = Nil | Cons Int Lint
Digression: curried vs uncurried functions
We have't talked yet about the arrow constructor. Consider the space of monotonic, continuous functions from
AtoB:A -> B
Proposition:
A * B -> Cis isomorphic toA -> B -> CProof: homework
Math:
ML and Haskell:
What is summed may vary:
Product operator is n-ary and fields are unnamed
Treatment of products may vary:
Recursion is always mediated by a data declaration
Is this function guaranteed to terminate?
(* SML *)
fun intlength Nil = 0
| intlengh (Cons (n, ns)) = 1 + intlength ns
(* Haskell *)
intlength Nil = 0
intlength (Cons n ns) = 1 + intlength ns
Answers:
In SML, yes: this is the principle of structural induction
In Haskell, NO: Haskell types are defined coinductively
For coinduction, see section 1 of the tutorial paper by Andy Gordon.
Intuition: the largest set satisfying the equations.
The meaning of recursion:
In ML, a datatype is defined inductively: the type is the least (smallest) solution to the recursion equation.
In Haskell, a datatype is defined coinductively: the type is the greatest (largest) set solving the recursion equation.
In ML and Haskell, recursion at the value level (distinct from type) is always inductive (least fixed point).
Question: Let Linf be the set of all finite and infinite lists
of integers. Does Linf solve
Linf = 1 + Int * Linf ?
Question: Suppose you wanted to define a set containing only the infinite lists of integers (no finite lists). What recursion equation would you write?
Worlds of infinite values:
Both semantics and code have a word for this: "bottom"
|
One notation, many meanings:
New partial order: refinement
Refinement comes with its own:
Consider this recursion equation, in the value domain of lists of integers:
lintmap f Nil = Nil
lintmap f (Cons n l) = Cons (f n) (lintmap f l)
e = 0 `Cons` lintmap (2+) e
What is e?
Fixed-point construction!!! Starting at _|_.
Least and greatest fixed points:
I did the proofs using Andy Gordon's tools.
Pretty easy: least (inductive) proof was constructive; greatest (coinductive) proof was by contradiction.
Do you want to do these proofs?
Real truths about Haskell:
I went to the experts.
The experts spake with forked tongue.
If you're willing to pull the bottom element like a rabbit out of a hat, and if you're willing to engage in a lot of mystical juju like
LI = (1 + (Int * LI)bot)bot
then you can recover Haskell types using induction rather than coinduction, and moreover (at least in some cases) you can prove that the greatest and least fixed points are the same.
I found this grotesque!
On coinduction, the jury is still out.
The handout is gobbledegook.
syntactic vs semantic fixed point
weak head normal form
thunks
Do you want another?
Parametric polymorphism in math:
List(A) = 1 + A * List(A)
Parametric polymorphism in Haskell:
data List a = Nil | Cons a (List a)
Special notation for built-in lists!
data [a] = [] | : a (List a)
Context (looking ahead):
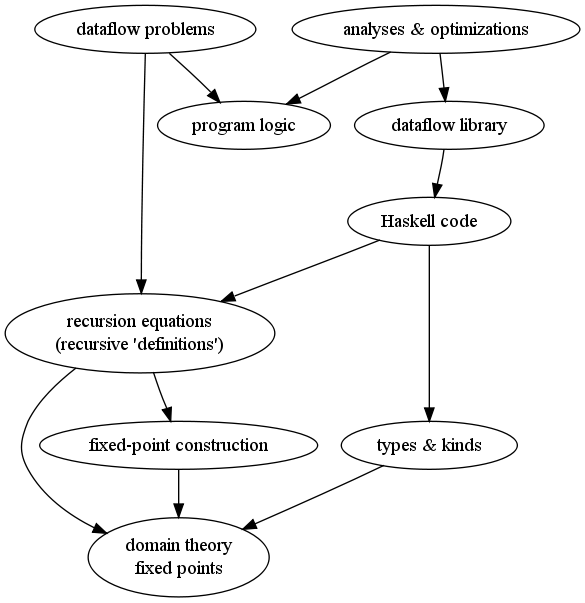
Coming attraction: Concept map
Foundations:
Consider this definition:
data Maybe a = Nothing | Just a
What functions have type
forall a . Maybe a -> Bool
Discover by type-directed programming
Polymorphic functions on lists:
p :: forall a b . (a -> b) -> [a] -> [b]
q :: forall a . (a -> Bool) -> [a] -> [a]
r :: forall a . (a -> Bool) -> [a] -> Bool
u :: forall a b . b -> (a -> b -> b) -> [a] -> b
Type-directed development:
p :: (a->b) -> ([a]->[b])
Introduction rule for arrow:
Gamma, x : tau |- e : tau'
-----------------------------
Gamma |- \x -> e : tau -> tau'
So to make a value arrow type, lambda!
p = \ (f::a->b) -> hole
where hole :: [a] -> [b]
Similarly, hole has arrow type
hole = \as -> hole'
Now what is the type of as?
What is the elimination form for an algebraic datatype?
hole = \as -> case as of
[] -> empty
a:as -> nonempty
What's the type of nonempty?
How could we possible produce a value of that type?
Does it use all the arguments?
OK, what about nonempty? What are the arguments in scope we need to use?
How can we use them?
What do we want in the result?
What is the introduction form for an algebraic data type?
What's the right constructor in this case? At what type should it be used?
Principles of type-directed programming:
Driven by
If the required type has a unique introduction form (arrow, product), use it.
If the required type has multiple introduction forms (any
algebraic data type with multiple constructors), then look for a
form which consumes case-bound or lambda-bound variables in
the environment.
To consume a value, look for
Arrow: introduced by lambda and eliminated by application
Product (rare): introduced by (x1, x2) and similar; eliminated by
let binding
Sum (algebraic data type): introduced by constructor and eliminated by
case.
Syntactic sugar!
Instead of
length = \l -> case l in [] -> 0 _:xs -> 1 + length xs
Absorb lambda in to definition:
length l = case l in [] -> 0 _:xs -> 1 + length xs
Convert top-level case into multiple equations (most idiomatic!):
length [] = 0 length (_:xs) = 1 + length xs
More syntactic sugar: special elimination form for Bool:
Instead of
case e of True -> e1
False -> e2
we write
if e then e1 else e2
So, all we really have in Haskell is
letwhereIn class: Design a Haskell data type to represent formulas in propositional logic. You have choices.
In class: Design a Haskell data type to represent formulas in each of the following normal forms:
In class: Derivations for q, r, and u. None are uniquely determined, but
some have an obvious "best simple" implementation.
Homework: Haskell finger exercises
Concept map:
You can see Norman and John's concept map in PDF or SVG:
Norman also wrote up a partial glossary of concepts.
Important Haskell constructs:
import ... hiding (...)import qualifiedrewriting declaration form
f = \x -> case x of p1 -> e1
...
pn -> en
to the more idiomatic declaration form
f p1 = e1
...
f pn = en
where clauses attach local declarations to a declaration form
let expressions attach local declarations to an expressionUseful ideas in the space of Boolean solvers:
Treating an assignment as something formed by the initial algebra of
empty :: Assignment
extend :: Variable -> Bool -> Assignment -> Assignment
By changing Bool to Value, this idea can be extended to
environments.
Type-directed programming leads to a unique, simple solution for
solve:
solve f = listToMaybe $ filter (sat f) $ allAssignments $ freeVars f
It's hard to create this solution from scratch; it's a little easier to name some of the intermediate results. The solution can also be written more in Hughes's style:
solve f = (listToMaybe . filter (sat f) . allAssignments . freeVars) f
Using list comprehensions to implement allAssignments:
allAssignments [] = [empty]
allAssignments (x:xs) =
[extend a x b | b <- [True, False], a <- allAssignments xs]
Paper, Tony Hoare: Axiomatic Basis for Computer Programming
Rules:
Axiom of assignment {P with e for x} x := e {P}
Rule of consequence
Rule of composition
Rule of iteration
Computational method (Dijkstra): weakest preconditions
Example: insertion sort
ASCII art:
0 j k n
+-------------------------+ +----------+ - - - - - - - +
| | | | |
+-------------------------+ +----------+ - - - - - - - +
This lecture was delivered impromptu in response to students' questions.
Monads allow one to encapsulate computations and run them in sequence. A computation "does something" and then produces a result.
Every monad must provide return and >>= (bind) operators
The type-class declaration
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
introduces overloaded operators
return :: Monad a => a -> m a
(>>=) :: Monad a => m a -> (a -> m b) -> m b
The type variable m has kind * => *.
The computation return x does nothing and produces x
The computation c >>= k first does c's computation,
returns a result x, then does the computation k x and
returns its result.
The operations obey monad laws:
c >>= return is equivalent to creturn x >>= k is equivalent to k xThe return and bind operations are not enough to have useful
computations. For additional utility, each monad general provides
specific primitives, and usually a "run" operation. (The IO monad
is unique in not providing a run operation within the program.
Instead, the value of main has type IO (), and the Haskell runtime
system runs the IO action.)
Example IO primitives:
getChar :: IO Char
putChar :: Char -> IO ()
Copy a character from standard input to standard output, forcing to upper case:
copyUpper :: IO ()
copyUpper = getChar >>= \c -> return (toUpper c)
This function can also be written using monadic do notation, which
makes the lambda-bound variables much easier to read:
copyUpper = do c <- getChar
return (toUpper c)
We then discussed the state monad:
type StateMonad a = State -> (State, a)
We implemented return and bind operations, and we also defined some of these primitives:
get :: StateMonad State
put :: State -> StateMonad ()
run :: StateMonad a -> State -> a
Also observe
run' :: StateMonad a -> State -> State -- run computation, ignore result,
-- and return final state
run' c = run $ c >>= \_ -> get
Finally, after class, Eddie asked about using this in the simplifier. Norman suggested
simplify' :: Exp -> StateMonad Exp -- uses 'put' but never 'get'
finish :: a -> StateMonad (Maybe a)
finish answer = do s <- get
case s in HasChanged -> return $ Just answer
Hasn'tChanged -> return Nothing
Then we can write
simplify :: Exp -> Maybe Exp
simplify e = run $ simplify' e >>= finish
No notes, no photos.
Algorithm: given a term e, return an environment Gamma and a type tau such that
Gamma |- e : tau
is a derivable judgement of the type system, and moreover, Gamma and tau are principal.
What does it mean to be principal?
Is a principal type unique?
An example: give principal typing of
if x == y then 1 else 0
(Converts Bool to Int.)
Let's take a closure look at the computation of the principal typing of
x == y
Final version of insertion sort (not complete; see photos)
void isort(int *a, int n) {
// PERM(a, in a) /\ n >= 0 -- precondition
int k = 0;
// OUTER INVARIANT:
// { PERM(a, in a) /\ SORTED[0..k) /\ 0 <= k <= n }
while (k != n) {
k = k + 1;
int j = k - 1;
int elem = a[j];
// INNER INVARIANT:
// { PERM(???, in a) /\ SORTED[0..j) /\ SORTED[j+1..k)
// /\ BOUNDS => elem <= a[j+1]
// /\ ???
// }
while (j != 0 && elem > a[j-1]) {
//
// ???
//
}
a[j] = elem;
}
}
SORTED[x..y)Definition:
SORTED[x..y) means forall i : x <= i < y-1 : a[i] <= a[i+1]Proof rules
SORTED[x+1..y) a[x] <= a[x+1] 0 <= x
------------------------------------------- Extend-Left
SORTED[x..y)
SORTED[x..y-1) a[y-2] <= a[y-1] y <= n
------------------------------------------- Extend-Right
SORTED[x..y)
SORTED[x..w) SORTED[w..y) a[w-1] <= a[w]
------------------------------------------- Split
SORTED[x..y)
Hoare triple for array assignment:
P[a |--> a with [j] -> e] { a[j] := e } P
Also written
P[a |--> update(a, j, e)] { a[j] := e } P
Where we have proof rules for indexing:
x = y
-------------------------
update(a, x, e)[y] = e
x != y
-------------------------
update(a, x, e)[y] = a[y]
Exercise: binary search
Solutions to binary search
Lattice of Boolean formulas
Given statement S, there are many triples
P {S} Q
Which one is the best?
Let us take Q, the goal, as given.
Using Hoare's implication rule, suppose we find
P' {S} Q
such that if
P {S} Q
then P' => P
Then P' is the weakest precondition of command S and
postcondition Q.
Table (as logical formulas)
A formula is a predicate describing sets of states.
Extend the view to sets
Q: In the Venn diagram, what are the weakest conditions?
(helps keep story straight)
Connection #1: our old friend the subset relation. So relative weakness/strength (impliciation) is a partial order.
The argument from logical formulas is dubious.
Suppose P1 and P2 are preconditions.
That is
P1 {S} Q
P2 {S} Q
what can we conclude?
Q: Given any two formulas P1 and P2, do they have a greatest lower
bound? That is
P1 => B
P2 => B
and
P1 => Q and P2 => Q then B => QYes!
P1 \/ P2I think this conclusion can be derived syntactically, without appealing to an underying model.
So let's conclude
P1 \/ P2 {Q} S
This is much easier to understand if we appeal to the underlying model of machine states!
Let's draw a picture...
Consider the infinite set of Pk such that
Pk {S} Q
Does an infinite set of formulas have a greatest lower bound?
<= suffices)A: No!
x = 3 or x = 5 or x = 7 or x = 11 or ...
Consider this definition:
wp(S, Q) is a predicate that represents the set of all
states such that if S is executed in any of the states, its
execution terminates in a state satisfying Q. (If termination
is not required, we have wlp.)Q: Does this set exist?
A: Yes! (by appeal to the model)
Q: Is it necessarily representable by a formula?
A: No! Consider a primality test. (And note decidability issues)
Conclusion: wp has to be approximated
How can we use wp to replace the proof system for P {S} Q?
P {S} Q, instead write P => wp(S, Q)Dataflow analysis is all about mutation and sequencing, so let's start there:
wp(x := e, Q) = Q[x |--> e]
wp((S1; S2), Q) = wp(S1, wp(S2, Q)) -- like continuations
wp(if B then St else Sf, Q) = (B /\ wp(St, Q)) \/ (!B /\ wp(Sf, Q))
or B => wp(St, Q) /\ !B => wp(Sf, Q)
We can check to make sure the two formulas are the same by enumerating the truth table:
class Predicate a where
tautology :: a -> Bool
instance Predicate Bool where
tautology b = b
instance Predicate b => Predicate (Bool -> b) where
tautology p = tautology (p True) && tautology (p False)
classf b t f = (b && t) || (not b && f)
nrf b t f = (b `implies` t) && (not b `implies` f)
same = tautology check
where check b t f = classf b t f == nrf b t f
implies p q = not p || q
The empty statment is traditionally written skip.
wp(skip, Q) = Q
Review of weakest preconditions: let's curry:
wp :: C -> Formula -> Formula
wp (Gets x e) = subst x e
wp Skip = id
wp (Seq s1 s2) = wp s1 . wp s2
wp (If c t f) = (const c /\ wp t) \/ (const (com c) /\ wp f)
This code compiles.
We have
class Predicate a where
(/\) :: a -> a -> a
(\/) :: a -> a -> a
com :: a -> a
instance Predicate Formula where ...
instance Predicate b => Predicate (a -> b) where
p /\ q = \f -> p f /\ q f
p \/ q = \f -> p f \/ q f
com f = com . f
Homework:
Design and implement a simple object language of assignments and expressions such that expressions are closed under substitution for variables.
Implement substitution.
We will provide sequencing and control flow.
Review: reduction of structured control flow to conditional and unconditional goto.
Idea: each label L is associated with a predicate P_L
wp(goto L, Q) = ???
wp(if B then goto Lt else goto Lf, Q) = ???
Consider this loop
while n > 0 do n := n - 1 end
What is
wp(while n > 0 do n := n - 1 end, n = 0)?
Break down to basic blocks
Loop:
if n > 0 then goto Body else goto End;
Body:
n := n - 1
goto Loop;
End:
To compute
wp(while n > 0 do n := n - 1 end, Q),
Each basic block contributes a recursion equation:
Here Q is n = 0
At the board:
We computed
wp(while n > 0 do n := n - 1 end, n = 0),
in several steps:
Break the loop down into basic blocks
Loop:
if n > 0 then goto Body else goto End;
Body:
n := n - 1
goto Loop;
End:
Each basic block contributed a recursion equation
By substitution, got a recursion equation for
P_Loop = (n > 0 /\ P_Loop [n -> n - 1]) \/ n = 0
Solved by successive approximations:
P0 = true
P1 = (n > 0 /\ true) \/ n = 0
= n >= 0
P2 = (n > 0 /\ (n>=0)[n |-> n - 1]) \/ n = 0
= (n > 0 /\ (n-1>=0)) \/ n = 0
= (n > 0 /\ (n>0)) \/ n = 0
= n > 0 \/ n = 0
= n = 0
Special-case algorithms exist for
structured programming
structured programming with nonlocal exit
so-called reducible control-flow graphs
But it's pretty easy to solve the general case
General case arises out of the nature of the von Neumann machine
control-transfer instructions (branch, conditional branch, computed branch)
branch targets
computational instructions
control transfers and computation can be observed
branch targets are either given by the compiler, recovered through analysis, or in the case of JIT compilation, garnered through observation.
Program logic hinges on predecessors and successors.
(Many/many is obtained through composition; we rule it out to keep compilers simple---there are no foundational difficulties.)
Exercise at the board: how do weakest preconditions work, in the general case, for each of these three kinds of constructs? (Hint: the results of computing wp is a set of recursion equations.)
Arbitrary sequence of assignment, control transfer, label
Main step is to * replace fall through with conditional branch*.
Program as regexp (Assignment, Branch, Label)
(A*(BL))*A*
Not very insightful. But let's refactor:
(A*B)? (LA*B)* (LA*)?
We now have entry, body, exit. Notice
all loops occur within the body
*the body is a collection of basic blocks LA*B *
within the body, order of blocks is irrelevant to semantics,
Finally, labels are unique
Assignment at board: reduce insertion sort (printout) to basic blocks.
Weakest preconditions are about goal-directed programming:
Start with some postcondition we are trying to established (the array is sorted).
Put some command in front of that postcondition to get to a precondition that is easier to establish.
Eventually we will get to a precondition that is so weak that it is trivially established by a procedure's entry condition.
Presto! We have constructed a procedure.
As a method of software construction, this is ideal: we reason backward from a known goal to something easily established.
Problem: the compiler seldom has a goal in mind, and when it does, has no guarantee the goal and be achieved.
Mathematically unsatisfying:
Given P {S} Q, we fixed S and Q and spent all this time
varying P. But why not try the following?
P {S} Q
^ ^ |
| | V
This is the method of strongest postconditions.
If weakest pre is about what we are trying to achieve, then strongest postconditions is about what we can conclude from the code we're given.
Problem: define the predicate transformer sp. (include assertions)
Note: By far the most difficult issue is what to do about an assignment
x := e. In particular, what happens to our knowledge about the previous value ofx?
No analog of P {S} Q. Instead, basic blocks:
\ | /
L
|
Asst
|
Asst
.
:
Asst
|
Branch
/ | \
L1 L2 L3
Method for analysis:
Associate a formula with each label
Compute recursion equations
Solve recursion equations by method of successive approximations
Questions:
When computing weakest preconditions, what names appear on the
right-hand side of the formula associated with label L?
When computing strongest postconditions, what names appear on the
right-hand side of the formula associated with label L?
What is the algorithm for taking a set of basic blocks and computing a set of recursion equations using strongest postconditions?
(Encompasses rules for labels and branches)
Strongest postcondition may imply that assertion always holds.
void isort(int *a, int n) {
L0:;
int k = 0;
goto L1;
L1:
if (k != n) goto L2; else goto L3;
L2:
k = k + 1;
int j = k-1;
assert(0 <= j && j < n);
int elem = a[j];
goto L6;
L6:
if (j != 0) goto L7; else goto L5;
L7:
assert(0 <= j-1 && j-1 < n);
if (a[j-1] > elem) goto L4; else goto L5;
L4:
assert(0 <= j && j < n);
assert(0 <= j-1 && j-1 < n);
a[j] = a[j-1];
j = j - 1;
goto L6;
L5:
assert(0 <= j && j < n);
a[j] = elem;
goto L1;
L3:
return;
}
Can the compiler tell if array access is in bounds?
Note: Hoopl is not quite ready for use.
Focus on approximation of facts:
Constant propagation (as in the paper from July)
Induction-variable elimination (also from July)
Lecture: GADTs and open/closed nodes; algebra of control-flow graphs
Array-bounds checks to wait.
A lattice is a partial order with two operations (meet and join)
least upper bound == join == sup == vee (corresponds to forward data flow)
greatest lower bound == meet == inf == wedge
I can never remember the meaning of meet, join, vee, wedge. I stick with "lub" and "glb", or if I'm feeling daring, "sup" and "inf".
What makes it a lattice is that inf and sup are always defined.
A bounded lattice also has the two distinguished elements top and bottom, each of which is related to all the elements in the lattice.
Any finite lattice is automatically bounded. If you get an infinite unbounded lattice you can always get a bounded lattice by a there is always a top and bottom.
The powerset of any set forms a bounded lattice.
Given any lattice L', I can construct a new lattice L' which is
L "turned upside down."
Thus, what you view as top and bottom is purely a matter of
convention.
No end of confusion.
Compositional approximation of a general formula in the lattice:
A[| TRUE |] = T
A[| FALSE |] = _|_
A[| f /\ f' |] = A[| f |] `inf` A[| f' |]
A[| f \/ f' |] = A[| f |] `sup` A[| f' |]
A[| x = k |] = [ x |--> Const k ]
A[| k = x |] = [ x |--> Const k ]
A[| all others |] = T
Disjunctive normal form may lend intuition but it is superfluous.
Implementation using the Presburger package, but the package is not entirely helpful...
Show the code
Hoare logic ignores history:
Open/closed; algebra of control-flow graphs
Dataflow logic can remember information about paths:
Postorder depth-first numbering
Identifying loop headers
Work at the board computing reaching sets and dominators.
Plan for Weds:
Start at 1.30
NR will open by explaining ideas, graph, node, lattice, transfer functions, rewrite functions
Each team 25 minutes + 5 minutes for questions.
Finish at 4pm (realistically, 4.15).
I will* cut you off after 25 minutes, so **you must practice for timing.
Code is OK, ideas are OK, results are OK
Two or three jury members:
Glenn Holloway, Harvard research staff, worked for several years on reusable optimizers using C++. He will like the simplicity and elegance of the Haskell approach.
Jan Maessen, Google, expert in Haskell, compiler project part of dissertation.
Olin Shivers, Northeastern, quirky, teaches compilers in Standard ML (similar to Haskell), invented control-flow analysis for higher-order languages. He will like this stuff.
Be interesting. Think about what you would tell Professor Guyer.
PRACTICE!
Presentations will be in Halligan 108. Directions to Halligan are online at http://www.cs.tufts.edu/~nr/directions/; visitors, please try to arrive by 1:20, or if you will be driving and need a legal place to park your car, please arrive by 1:10.
To get to the classroom, enter Halligan at the front door (where it says "Department of Athletics Electrical Engineering and Computer Science"), walk past the stairs and down the hall until the hall turns. 108 is the corner on the outside of the building to your left.
If you are driving, park your car in the Dowling Hall garage on Boston Avenue just north of College Avenue. From Dowling, walk a half block southeast to College Avenue and turn left. Continue on College Avenue and cross the railway line. Halligan Hall is the large brick building on your left (it's a former radio factory).
If you drive, when you enter Halligan, go immediately left to the Computer Science office and ask for a parking token. This token will enable you get out of Dowling free. You can then proceed to the classroom.
The schedule for the afternoon is as follows:
| When | Who | What |
| 1:30 | Norman Ramsey | Introduction to Hoopl |
| 2:00 | Chris Rice | Testing Hoopl clients |
| 2:30 | Eddie Aftandilian, Nathan Ricci | Testing optimizations |
| 3:00 | Sound Bites | Break |
| 3:15 | John Mazella | Lazy Code Motion |
| 3:45 | Jessie Berlin, John Sotherland | Strength Reduction and Induction Variables |
| 4:15 | Everyone | Mingling |
| 4:30 | — | Event ends |
Visitors who are able are invited to stay for dinner.
Discussion of how to think about strength reduction and induction variables at a higher level of abstraction than Cocke and Kennedy.
Further discussion of loops and how to identify them.