Simulate an HMM

First, build an HMM simulator so that you have a source of ``observations'' and a target to compare against. To do this, we will build an MM, and then we will proceed to ``hide'' it from the HMM trainer. I suggest creating code that can manage N states, numbered 0, ...  N - 1, and M different kinds of observations, numbered 0, ...  M - 1, and which produces observations of length T. In other words, N, M and T are parameters of your Markov model. 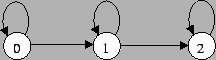Initially, I suggest that we attempt to train models where N = 3, M = 4 and T varies from 3 to 5. Here is an example.

If this above model splits its transition probabilities 3:1 in favor of going ``right'', then the transition probability matrix is as follows.

ai, j	0	1	2
0	0.25	0.75	0
1	0	0.25	0.75
2	0	0	1.0

Let's assume that this model always starts in state 0.

$\pi_{i}^{}$	0	1	2
	1.0	0	0

Finally, there are four observations, 0, 1, 2 and 3, with the following probabilities per state.

bi(k)	0	1	2	3
0	0.5	0.5	0	0
1	0	0.5	0.5	0
2	0	0	0.5	0.5

To build the MM, use a Monte Carlo simulation. First, you'll need a random number generator. In C, use the random() function (see manual page), seeded by srandom() using the data from a call to time() (see manual page).¹ Once random() is seeded, you can easily define a function randomint(lb, ub) that returns a random integer x in the range lb$\leq$ x <ub.²

  int randomint (int lb, int ub) { 
     return lb + random() % (ub - lb); 
  }

You can also define a function that returns a random floating point number x in the range 0 $\leq$ x $\leq$ 1.

  double randomreal () { 
     return ((double) random()) / RAND_MAX; 
  }

To generate a random choice over a given distribution, simply do the following. Assume we wish to generate the initial state according to $\pi$.

1. Generate a random number x such that 0 $\leq$ x $\leq$ 1.
2. i $\leftarrow$ 0.
3. x $\leftarrow$ x - $\pi_{0}^{}$
4. While i < N and x > 0 do
5.    i $\leftarrow$ i + 1
6.    x $\leftarrow$ x - $\pi_{i}^{}$
7.   End while loop.
8. If i < N then i is the randomly selected state else error (sum of probabilities is < 1).

Use the above method to:

• select the initial state of the HMM,
• select the next state, and
• select the observation that appears in each state.

You are now ready to define a function that produces a single observation sequence.

function newsequence ( N, M,$\pi$, a, b, T)

1. Create an HMM according to the given model.
2. Let s be the initial state, chosen according to $\pi$.
3. Let O be the empty sequence of observations.
4. While length(O) < T do
5.   Let o be the observation for current state s, chosen according to b_s.
6.    O = concatenate(O, o) (i.e., add o to the end of O).
7.    s $\leftarrow$next state according to a_s.
8.   End while loop.
9. Return O.