This homework is due at 11:59PM on Wednesday, November 6. Submit your solutions in a single file using the COMP 50 Handin button on DrRacket; the homework is the abstract homework.

All the exercises should be done using the Intermediate Student Language.

This homework is challenging, which is why you have extra time for it. I recommend that you find a study partner or a TA and that you work some of the finger exercises. If you post a finger exercise to Piazza, I will do my best to give you feedback.

Finger exercises

From the first edition, I recommend these finger exercises:

• 19.1.5, 19.2.4
• 20.2.2, 20.2.4
• 21.1.1, 21.1.2
• 21.2.3

And also these exercises:

• Use local definitions to simplify my hours-display function from the Part I of the Structures homework.

• Use abstraction to define a single function that can replace both the congratulations and consolation functions from my solution to the Fitts’s Law problem (Part II of the Structures homework).

• Use abstraction to combine functions sort-up and sort-down from my solution to the fish-division problem from the homework on self-referential data. Define insert as a local function.

Problems to submit

Using local to contain costs

1. Copy the solution to pascal-nums from the templates homework. Try these expressions in the Interactions window:

   > (time (pascal-nums 17))
   > (time (pascal-nums 18))
   > (time (pascal-nums 19))

   Now use local to change the running time. You will be reducing the running time from exponential (2^N) to quadratic (N²). Try these expressions in the Interactions window:

   > (time (pascal-nums 17)))
   > (time (pascal-nums 18)))
   > (time (pascal-nums 19)))
   > (time (second (pascal-nums 100)))
   > (time (second (pascal-nums 200)))
   > (time (second (pascal-nums 300)))

   Finally, I give you a 3000-millisecond time limit. Staying within that limit, please measure how long a list you can compute with the fast version of pascal-nums.¹

   Submit the fast version of pascal-nums, along with the outcome of your measurement.

Using abstraction to eliminate repetitious code

2. On the mutual-reference homework, you wrote three different functions to determine nesting depth of ordered lists, nesting depth of unordered lists, and nesting depth of all lists. Using the abstraction and simplification techniques from Section 21 (Designing Abstractions from Examples), define a single function that can replace these functions, possibly with the addition of a few helper functions.

Parametric data definitions

3. The function condense turns lists of lists of things into lists of things. Here are some functional examples:

   (check-expect (condense '((1 2) (3 4 5) () (6 7)))
                 '(1 2 3 4 5 6 7))
   (check-expect (condense '(("Dear") ("Mr" "Ramsey") ("your" "frog" "died")))
                 '("Dear" "Mr" "Ramsey" "your" "frog" "died"))

   Using the parametric data definition for lists, write a signature, purpose statement, and header for condense.

4. Here is a self-referential data definition:

   A number-bst (binary search tree of numbers) is either:

   • false

   • A structure

     (make-node left key value right)

     where key is a string, value is a number, left is a number-bst in which all keys are less than this key, and right is a number-bst in which all keys are greater than this key.

   An image-bst (binary search tree of images) is either:

   • false

   • A structure

     (make-node left key value right)

     where key is a string, value is an image, left is a image-bst in which all keys are less than this key, and right is a image-bst in which all keys are greater than this key.

   In both data definitions, “less” and ’greater" are determined by string<?; they basically amount to alphabetical order. If you want to understand the details, you can experiment with DrRacket’s Interactions window.

   This problem has three parts:

   1. Generalizing from the two example definitions above, write a parametric data definition for binary-search trees that can be used to store any given class of value.

   2. The “search” in a binary-search tree comes from a function that is given a binary-search tree and a string key. The function searches for a node containing that key, and if it finds such a node, it returns the node’s value. If it does not find the node, it returns false.

      Using your parametric data definition from the previous problem, write the signature, purpose statement, and header for a function that searches binary-search trees. The signature must have one or more type variables.

   3. Using the design recipe for self-referential data, finish the design of the function for searching in a binary-search tree (from the previous problem). Make sure that your test cases use the function with different types of values.

   This problem is similar to the search on the apocalyptic railway, but it is significantly easier.

5. Here are two parametric data definitions:

   A (2Dpoint X) is a structure

   (make-point x y value)

   where x and y are numbers and value is an X.

   A (2Dtree X) is one of the following:

   • A (2Dpoint X)

   • A structure

     (make-v-boundary left x right),

     where

     • x is a number,
     • left is a (2Dtree X) in which every point has an x coordinate at most x, and
     • right is a (2Dtree X) in which every point has an x coordinate at least x

   • A structure

     (make-h-boundary above y below),

     where

     • y is a number,
     • above is a (2Dtree X) in which every point has an y coordinate at most y, and
     • below is a (2Dtree X) in which every point has an y coordinate at least y

   Here is an image derived from a data example made using make-v-boundary: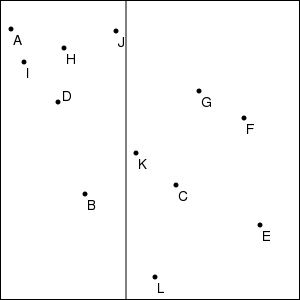
   

   And here is an image derived from a data example made using make-h-boundary:
   

   This problem has two parts:

   1. Based on the simple maps used for the templates homework, write data examples for (2Dtree string). A list of towns appears at the end of the problem, but you need not include every town.

   2. Define a function nearest-point which is given the (x, y) coordinates of a “target” and is also given a (2Dtree X). The function returns the (2Dpoint X) within the tree that is closest (in ordinary Euclidean distance) to the target.

      Your function must avoid searching on the far side of a boundary unless such a search is necessary. To figure out when a far-side search is necessary, use the table you made for the templates homework (or my solution).

   The second part of this problem presents a major design challenge. To help you meet this challenge, here are some observations about templates, conditionals, helper functions, and testing:

   • If you don’t know your templates, or if you are not scrupulous about following the design recipe, you will die of frustration. Know your templates.

   • Treat conditionals like gold: spend as few of them as possible.

   • The function nearest-point consumes only one piece of complex data, which is defined by choices. There are three choices, so you can expect a conditional with three cases.

   • When you’re dealing with a boundary, one subtree has coordinates that are smaller than the location of the boundary, and the other side has coordinates that are at least as large as the location of the boundary. But because you’re searching for the point nearest the target (x, y), there’s a more important distinction.

     • The subtree on the same side as the target is called the near subtree.

     • The subtree on the opposite side as the target is called the far subtree.

   • To tell which subtree is “near” and which is “far”, you will need another conditional.

   • “Near” and “far” are good words to use to form names used in local definitions.

   • In your main function, do not nest conditionals deeper than two, or nobody will understand it. If you need other conditionals (and you will), put them in helper functions.

   • The presence of so many conditionals means you will have to craft your test cases carefully, and you will need more test cases than usual. Make sure that when you press the Run button, that there is no untested code.²

   • Use local definitions for both values and functions. For example, the near and far subtrees are potential candidates for local definitions.

   • You always have to search for the nearest point in the near subtree. Use the appropriate natural recursion.

   • As you know from the templates homework, you may or may not have to search across the boundary in the far subtree. The key to efficiency is to search the far subtree only when necessary. The job of “searching only when necessary” is best given to a helper function. At minimum, this helper function needs to know

     • What is the far subtree?
     • What is the closest point in the near subtree?
     • How far away is the boundary?

     This function also needs to know the (x, y) coordinates of the target point. If you make this function a local function, it can access these coordinates directly. Or you can choose to make it a top-level function, in which case you can test it with check-expect. Both tactics have their advantages.

   • If you do have to search the far subtree, your final answer comes down to choosing whichever of two points is closer to the target (x, y) coordinates. For this job, I recommend designing yet another helper function.

   • The formula for Euclidean distance is annoying to write and even more annoying to read. I recommend that you arrange for it to occur in your code only once. If you need to design a helper function that calculates Euclidean distance, it’s OK.

   To help you create data examples and test cases, here is a list of all the towns from the maps used in the templates homework:

   (list
    (make-point 11 29 "A")
    (make-point 85 194 "B")
    (make-point 176 185 "C")
    (make-point 58 102 "D")
    (make-point 260 225 "E")
    (make-point 244 118 "F")
    (make-point 199 91 "G")
    (make-point 64 48 "H")
    (make-point 24 62 "I")
    (make-point 116 31 "J")
    (make-point 136 153 "K")
    (make-point 155 277 "L"))

   Once you have a good template, I don’t expect the code itself to give you much trouble, but if at any point you get stuck, here are some useful questions. You should base your answers on the results for the map examples on the templates homework.

   • Which side of the boundary is the near side?
   • How do you know?
   • Which side of the boundary do you have to search first?
   • How do you code that search?
   • Do you have to search the far side of the boundary?
   • How do you know?
   • If you have to search the far side of the boundary, how do you code that search?
   • What searches do the natural recursions correspond to?
   • If you only have to search the near side of the boundary, then what is the closest point?
   • If you have to search both sides of the boundary, then how do you determine the closest point?

Karma problem

There is one karma problem. It uses the following data definition:

• A bounding-box is a structure:

  (make-bb left right top bottom)

  where left, right, top, and bottom are numbers, and furthermore

  • (<= left right)
  • (<= top bottom)

  We say that a point (x, y) lies within a bounding box if x is between left and right and y is between top and bottom.

The problem is to define a function that is given a bounding-box and a (2Dtree string) and returns an image of that portion of the tree which lies within the bounding box. The image should include not only the points but also the horizontal and vertical lines marking boundaries.