7 October 2013: More lists and trees; designing
Today:
- More trees and lists
- Enriched design recipe for self-referential data
- The essential and the incidental
Coming attraction:
- Multiple complex inputs (e.g., two lists)
The railway tree
(define nyp (make-stn "NY Penn Station" 228.7))
(define nro (make-stn "New Rochelle" 212.1))
(define nhv (make-stn "New Haven" 156.4))
(define pvd (make-stn "Providence" 42.6))
(define bby (make-stn "Back Bay" 1.1))
(define bos (make-stn "South Station" 0))Live demo: how to make a tree
Functions:
southmost- imagine
northmost stations-onthe railway; theappendfunction
Note:appendis our first function that consumes two lists. (Built into BSL)- Checking
stations-on:south-to-north? - But first,
decreasing? - But first,
singleton?(used the enriched recipe)
List design:
- Lists of two or more elements
- The enriched recipe
The Essential and the Incidental
What are you learning?
- A foreign language: Beginning Student Language, which comes with
- vocabulary:
define,cond,define-struct,make-posn - grammar:
(define (f x) (+ (* 5 x) 22)) - meaning: the above is a function definition
- idioms:
(define dog (circle ...)), how to arrange functions
- vocabulary:
- Domain knowledge: the stuff we want programs to run on
- mathematics (e.g., probability)
- display rate for making movies
- geometry and trigonometry of navigation on the Earth’s surface
- Fitts’s Law
- …
- Computing knowledge: how does the meat grinder work?
- rules of arithmetic for symbols, strings, images, and numbers
- rules of function application: plug in argument for parameter
- rules of conditionals
- Computational problem solving through design
What do we think of all this?
Language is dominated by fashion (some languages are better for some purposes, but they don’t always win.
Vocabulary and grammar are rote learning. Fluency will come with time and practice. Lean on the manuals and the first Intermezzo.
Domain knowledge rocks. Every problem solver needs it. Sometimes (usually later in your career) you will work with a “domain expert.” For example, Professor Brodley works with radiologists to help teach the computer how to read X-rays and MRIs. But while you’re a student, and early in your career, or if you start a company, often you have to become the domain expert.
Start now. Take your hobbies seriously. Go deep into something that interests you—know more than anybody else.
The rules of computing are necessary. They become interesting when
As a last resort, you have to figure out what went wrong
- You need to know what things cost:
- Will it run on my PC?
- Will it run on my phone?
- Will it support a thousand users? A million?
- Will it handle big data? Cost is a big point of emphasis in COMP 15.
The key idea of this course is systematic problem solving. It helps you with business (courses), engineering, math, English, journalism, medicine, and other things. I guarantee it.
Roles:- Keeps 15h from turning into 30h
- By the end of the term, you won’t need a TA
Become a card-carrying member
6. Tests
5. Code
4. Template
3. Functional examples
2. Signature/purpose/header
1b. Data examples
1a. Describe data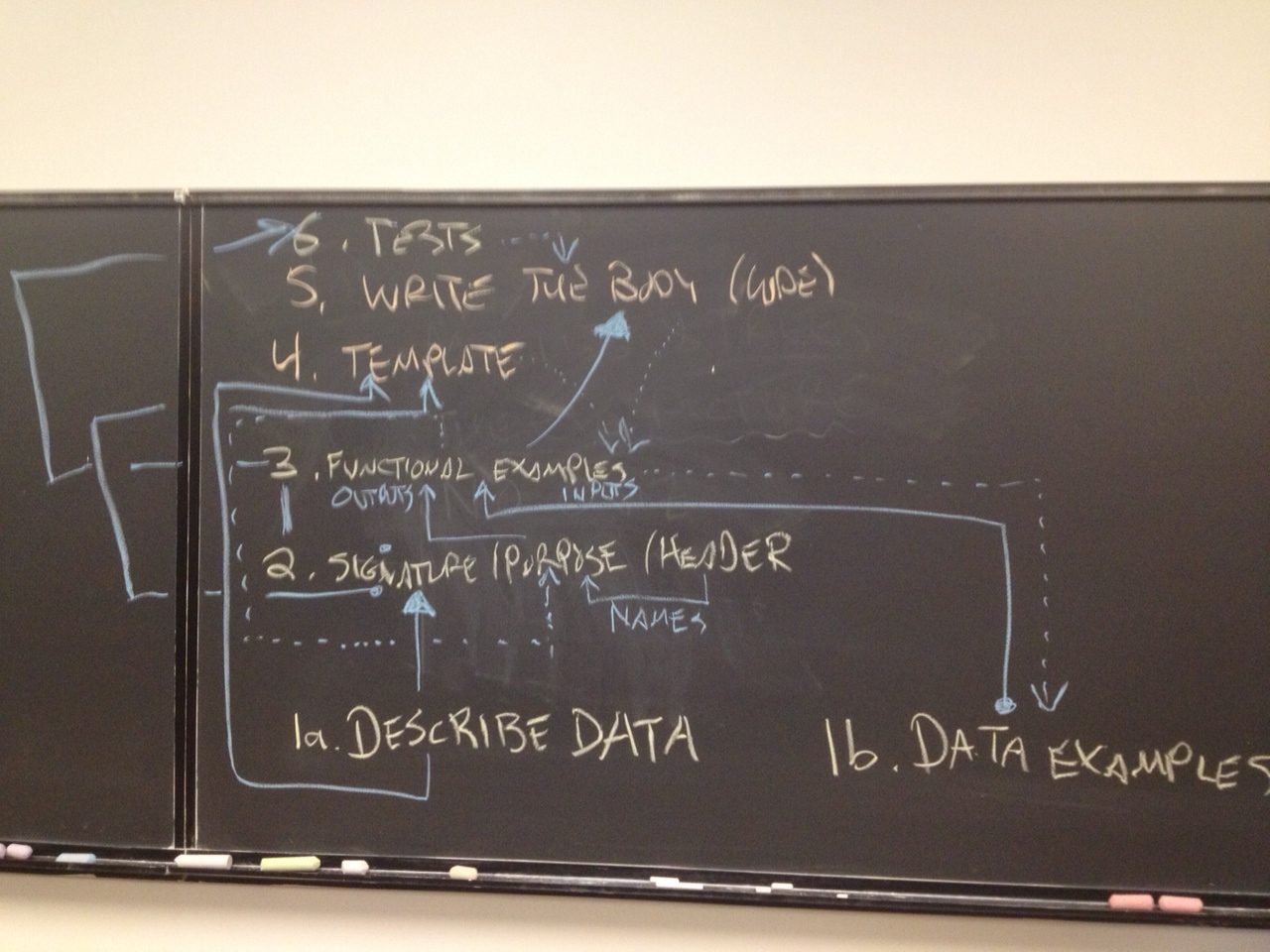
The design recipe from the bottom up, with feedback loops
The Grid
Add variants!
- cond cases with type predicates
forms of data
=============
| "atomic" | "enumerations" | "structure"
process steps | numbers, images, ... | intervals, strings | define-struct
===============-------------------------------------------------------------------
| | [1,3] (1,3) [1,3) | (make-posn 3 4)
describe data | Number Image | color is one of: .. | (make-dst "h")
----------------------------------------------------------------------------------
signature | Number -> Image | XYZ -> Number | ABC -> String
purpose | create sq of size s | convert into number | add "Dear" to name
header | (define (square s) ...) | |
----------------------------------------------------------------------------------
functional | 3 |---> [] | [1,3] |---> 2 | (make-posn 3 4)
examples | .... | ... | |--> "5"
----------------------------------------------------------------------------------
template | domain knowledge | cond cases! | selector expr.
----------------------------------------------------------------------------------
now code
----------------------------------------------------------------------------------
tests | turn examples into tests (use of check-expect)
| (check-expect (S 3) []) | (check-expect | (check-expect 5
| | (f 1 3) 2) | (f (make-posn 3 4)))
Interplay of the steps, e.g., in the line-drawing or circle-dropping programs.