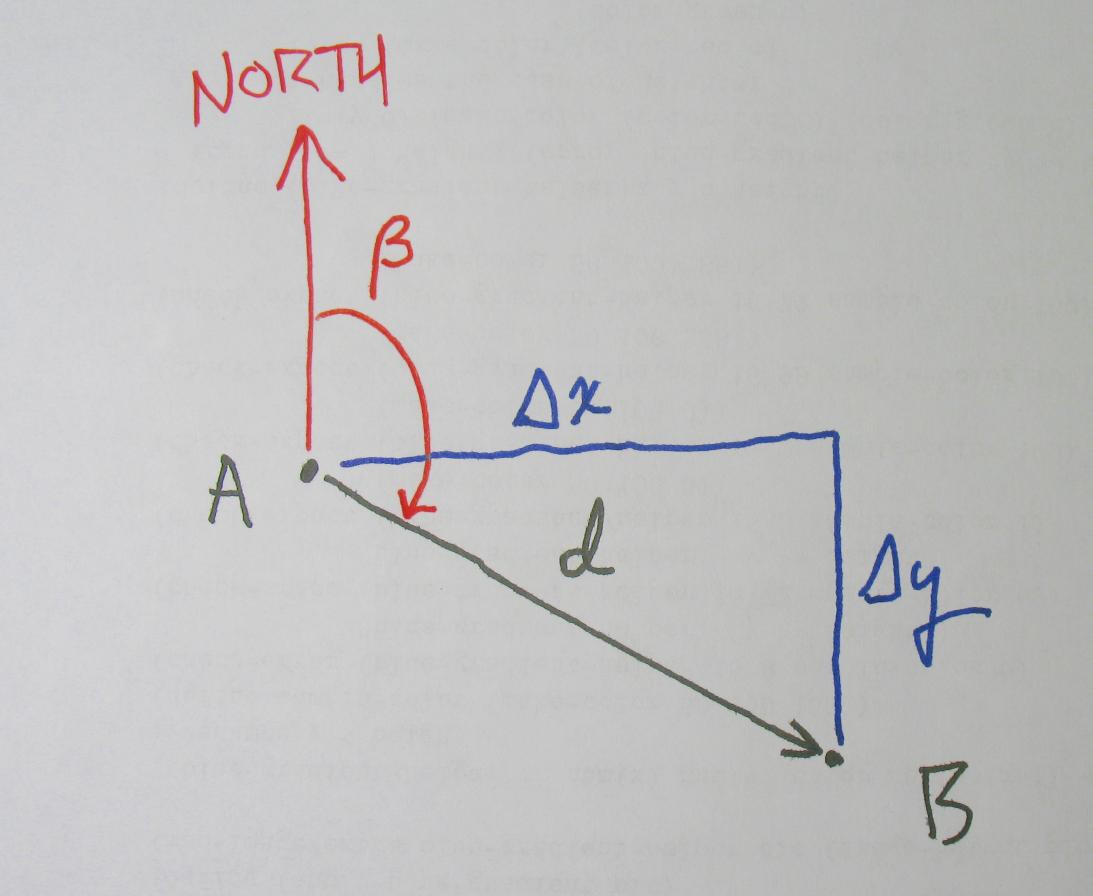
A step on the Earth’s surface from A to B
This handout contains all the math you need to do these tasks:
GPS projection over short distances, assuming the Earth is flat
Distance between two nearby points, assuming the Earth is flat
In all diagrams and equations:
θ is latitude (pronounced THAYT-uh)
ϕ is longitude (pronounced FEE)
β is bearing (pronounced BAYT-uh)
R is the radius of the Earth, which according to official geoid data is 6,378,137 meters.
Both distance and projection involve
A point A given by latitude θA and longitude ϕA
A point B given by latitude θB and longitude ϕB
The distance d between the points A and B
The bearing β of point B as seen from point A
The bearing is the angle made by a line drawn from A to B with another line drawn from A to the North Pole. Here’s a picture:

A step on the Earth’s surface from A to B
The homework has three computational problems related to this picture:
Given the two points A and B, which is to say the values of θA, ϕA, θB, and ϕB, compute the distance d between the two points.
Given the two points A and B, compute the bearing β of B as seen from A.
Given point A, which is to say the values of θA and ϕA, and given distance d and bearing β, compute the location of point B, i.e., θB and ϕB.
The first two problems can be solved using the following equations:
Δ y = R(θB − θA)
Δ x = RcosθA(ϕB − ϕA)
d2 = (Δ x)2 + (Δ y)2
β = arctan(Δ x / Δ y)
In case Δ y is zero, you want to use the two-argument arc-tangent function. In Beginning Student Language this is the atan function with two arguments. In the figure Δ x is about 60mm and Δ y is about -36mm and the bearing β is (atan 60 -36), which is about 120 degrees.
The third problem requires that you solve for θB and ϕB; given
I expect you to be able to solve for θB given R and Δ y, and similarly solve for ϕB given R and Δ x.
It is easy to get equations wrong. The only way you can know for sure is to test with actual locations. As a source of ideas you can make up your own coordinates, measure coordinates in the field, look up coordinates, or use Google Earth or Google Maps.
You can also use the Great Circle calculator at http://williams.best.vwh.net/gccalc.htm, but because the Great Circle calculator uses a more accurate model of the Earth, your answers will be off by a few percent.