Home People Papers & Presentations Courses Software Geometry Links

Reporting all intersections of line segments and their characteristics is one of the early and most fundamental problems in computational geometry. We concentrate on the problem of reporting all intersections in an embedding of a complete graph that may contain degeneracies such as vertical lines, or multiply intersecting lines, where the intersections along a segment need to be reported according to the order in which they are encountered. We apply our method to compute the simplicial depth median of a point set in R^2 [5].

A graph presents some difficulties for a sweep line algorithm that most of the existing sweep based algorithms do not handle. We present a novel approach that sweeps a complete graph of N vertices and k intersection points in optimal O(k)=O(N^4) time and O(N^2) space, that is simple and easy to code and resolves the difficulties in the graph sweep. The algorithm sweeps the graph using a topological line, borrowing the concept of horizon trees from the topological sweep method [4] and using ideas from [3] to deal with degeneracies. The novelty in our approach is the use of the moving wall that separates at any time the graph into two regions: the region of known structure, in front of the moving wall, and the region that may contain intersections generated by edges that have not yet been registered in the sweep process, behind the wall.

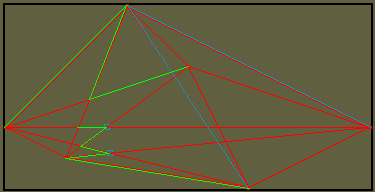
A snap-shot of the sweep line in a complete graph of 6 vertices. The green edges are the cut (topological line) edges. The blue squares are the vertices ready to be swept (ready vertices) and the blue lines are the moving wall associated with the current position of the sweep line.

[1]"Topologically Sweeping the Complete Graph" , E. Rafalin, D. Souvaine Proceedings volume related to the Cologne/Twente Workshop on Graphs and Combinatorial Optimization 2005, special volume of Discrete Applied Mathematics, submitted for publication, October 2005.

[2]"Topologically Sweeping the Complete Graph in Optimal Time and Space" , E. Rafalin, D. Souvaine, Tufts CS Technical Report, 2003-05

[3]"Topological Sweep in Degenerate cases", E. Rafalin, D. Souvaine, I. Streinu, Proceedings of the 4th international workshop on Algorithm Engineering and Experiments, ALENEX 02, in LNCS 2409, Springer-Verlag, Berlin, Germany, pages 155-156, Postscript version, Pdf version

[4]"Topologically Sweeping an arrangement", H.Edelsbrunner, L. Guibas, J. of Computer and System Sciences 38, 165-194, 1989

[5]"Algorithms for bivariate medians and a Fermat-Torricelli problem for lines", G. Aloupis, S. Langerman, M. Soss, and G. Toussaint. Comp. Geom. Theory and Appl. 26(1):69--79, 2003

A README file describing how to use the code.

A tar.zip version of the code.

Topologically Sweeping in degenerate cases

LMS regression in O(n²) time using guided topological sweep

This material is based upon work supported by the National Science Foundation under grants CCF-1422311 and CCF-1423615. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.