The Least Median of Squares (LMS) Regression Line of a point set is the line that minimizes the median squared residual. As a comparison, the more familiar ordinary least squares (OLS) regression line minimizes the sum of the squared residual. The advantage of the LMS line over the OLS line is that at least 50% of the data would need to be corrupt in order to skew the line (while for the OLS line, a single corrupt data point can give the resulting regression line an arbitrarily large slope).
We present an implementation of the guided topological sweep algorithm that computes the Least median of square regression line of a point set, based on the algorithm presented in [3].
The code deals with degeneracies in the data set and with multiple identical points. The implementation is based on minor modifications to this code.
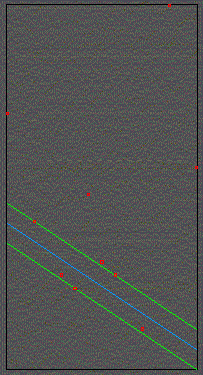
The green lines determine the smallest width slab that enclose 50% of the data points. The LMS regression line is the line exactly in the middle of the slab
[1] "Topological Sweep in Degenerate cases", E. Rafalin, D. Souvaine, I. Streinu, ALENEX 02, January 2002, San-Francisco, CA, Postscript version, Pdf version
[2] "Topologically Sweeping an arrangement", H.Edelsbrunner, L. Guibas, J. of Computer and System Sciences 38, 165-194, 1989
[3] "Computing Median-of-Squares Regression Lines and Guided Topological Sweep ", H.Edelsbrunner, D. Souvaine Journal of the American Statistical Association, 85, 1990, 115-119
A README file describing how to use the code.
A tar.zip version of the code - NEW - supports vertical slabs!
|
This material is based upon work supported by the National Science Foundation under grants CCF-1422311 and CCF-1423615. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. |
|