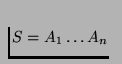 of n objects,
the sequence containing n-1 copies of S followed by
the first object A1 in S contains all permutations of the members of
A as subsequences. This sequence contains n(n-1)+1 elements.
of n objects,
the sequence containing n-1 copies of S followed by
the first object A1 in S contains all permutations of the members of
A as subsequences. This sequence contains n(n-1)+1 elements.
Given any set of scripts that are aware, convergent, and homogeneous, one can try them in all possible permutations in a very straightforward way. One exploits the following mathematical fact:
Proposition 5: Given a sequenceCounter to intuition, enumerating all permutations as subsequences of a given sequence does not require O(n!) steps, but only O(n2) steps.of n objects, the sequence containing n-1 copies of S followed by the first object A1 in S contains all permutations of the members of A as subsequences. This sequence contains n(n-1)+1 elements.
As an aside, this fact is easy to see by inductive proof. The
inductive basis case is that for two objects A1 and A2, the
appropriate sequence is A1A2A1. If we presume that the
proposition is true for
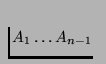 ,
then a sequence Sn-1 consisting of n-2 copies of
,
then a sequence Sn-1 consisting of n-2 copies of
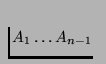 ,
followed by A1, contains all permutations of
,
followed by A1, contains all permutations of
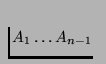 as subsequences. For An elements, we
construct the sequence Sn of n-1 copies of
as subsequences. For An elements, we
construct the sequence Sn of n-1 copies of
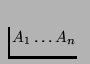 ,
followed by A1. Our claim is that Sn contains all permutations
of
,
followed by A1. Our claim is that Sn contains all permutations
of
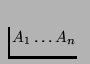 as subsequences.
as subsequences.
To show this, we choose one element Ai from the first copy of
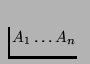 ,
and consider the subsequence of this
sequence constructed by starting after Ai and deleting Ai from the rest.
The beginning of this subsequence always has the form of
the sequence in the inductive hypothesis, and thus contains all
permutations of the A's without Ai. Thus the sequence Sn (of
which this is a subsequence) contains all permutations starting
with Ai. As Ai was arbitrary, Sn contains all permutations
of the A's.
,
and consider the subsequence of this
sequence constructed by starting after Ai and deleting Ai from the rest.
The beginning of this subsequence always has the form of
the sequence in the inductive hypothesis, and thus contains all
permutations of the A's without Ai. Thus the sequence Sn (of
which this is a subsequence) contains all permutations starting
with Ai. As Ai was arbitrary, Sn contains all permutations
of the A's.
For example, consider what happens with four scripts A, B, C, and D. If we start with the sequence ABCDABCDABCDA and select, e.g., C from the first group, the subsequence constructed according to the proof is ABDABDA, which has already been shown to contain all permutations of A, B, and D. By repeating this process we can generate all permutations of A, B, C, and D:
subsequence permutations ABCDABCDABCDA ABCD.BCD.B... (A first) .BCD..C...... ABCD, ABDC ..C..B.D.B... ACBD, ACDB ...D.BC..B... ADBC, ADCB .BCDA.CDA.C.. (B first) ..CDA..D..... BCDA, BCAD ...DA.C.A.... BDAC, BDCA ....A.CD..C.. BACD, BADC ..CDAB.DAB.D. (C first) ...DABA...... CDAB, CDBA ....AB.D.B... CABD, CADB .....B..A..DA CBAD, CBDA ...DABC.ABC.A (D first) ....ABC..B... DABC, DACB .....BC.A.C.. DBCA, DBAC ......C.AB..A DCAB, DCBA
This is not the best known solution to the problem of ``Permutation Embedding''. For n objects there is a sequence of n2-2n+4elements that contains all permutations of the original objects as subsequences[1,5,13,19,22,26,27]. The methods utilized to construct a sequence with this lower bound are less intuitive than ours, while the size of the sequence remains O(n2) in all cases. To our knowledge, finding the optimal solution in the general case remains an open problem in combinatorics.
In our case, the objects being permuted are scripts that manage the values of configurable attributes, while the sequence is the execution order for the scripts. If we know that a correct order for the scripts exists, then if we try to execute them in the order suggested above, that order will be achieved at some time during the process. Because of our homogeneity constraint, each script need work only once and scripts will not undo the work of others, so that one iteration of the scripts in the proper order is all that is required. Thus the precedence constraints for all scripts will be satisfied if there is a way to satisfy them at all, and the algorithm dynamically infers the correct execution order for the scripts as it executes.