Observability

The Maelstrom framework allows one to `glue together' several scripts toward a common goal. Precedences do not have to be specified during the gluing because Maelstrom will sort the scripts into an appropriate order during execution. During the sorting process, Maelstrom does not determine the actual precedences between scripts, but rather a total order that satisfies those precedences. The order is observable but the precedences are not[25]. Similarly,

Proposition 7: While the effects of homogeneity are observable, homogeneity itself is an abstract ideal that is unobservable in practice.

We will illustrate this fact with several examples.

For simplicity, let us consider the case in which all scripts control configuration attributes that have static values in the absence of script effects. This ignores dynamic attributes that can change on their own without script intervention. If the former are problematic, the latter surely are as well.

In this simplified model, there are only attributes to be controlled and parameters describing ideal settings. A configuration attribute is any such data, including text or numeric fields in configuration files or device memory, or even hierarchies of configuration data as handled by Arusha[17] or Babble[10]. A particular script can perhaps do two things with an attribute:

• read its value to validate this value against established norms.
• write a value into the attribute in order to put it into compliance with such norms.

The value of a particular attribute can be compared with a configuration parameter that describes its ideal state. This can either be a fixed value or a rule that describes the ideal value in a variety of situations.

Using this simplified model of script behavior, we can describe correct and compliant script behavior as well as possible deviant script behaviors:

• A script that is aware can read all the configuration attributes that it sets to check for success or failure.
• A script that is convergent only changes attributes that are ``out of sync'' with desired parameter settings. This means that it reads every attribute and writes it only if it does not satisfy parameter requirements or rules.
• A script that is homogeneous agrees with other scripts upon parameter values. This can be accomplished either by synchronizing the contents of multiple parameter sources or by depending upon a single source for parameter and policy information.

  

Figure 2: A healthy transaction copies a parameter into an attribute only if needed.

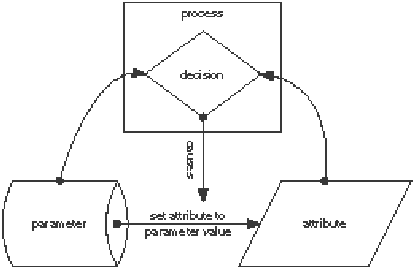
Graphically, the relationships between scripts, attributes, and parameters may be depicted by representing scripts as rectangles, decisions as diamonds, parameters (or policies) as storage drums, and device attributes to be controlled as parallelograms. An arrow between two objects means that the first affects the second, even when one or more of the objects being affected are themselves arrows. An arrow between a parameter and an attribute means that this parameter affects that attribute by setting it to a compliant value. An arrow from a script to the prior arrow means that the script in question enforces that relationship.

  

Figure 3: Two homogeneous scripts using the same parameter source.

  

Figure 4: Two inhomogeneous scripts using different parameter sources.

For example, in Figure 2, we have one healthy configuration process that controls one attribute with respect to one parameter. The process reads both the attribute and its controlling parameter, and the attribute is only set if needed. This is indicated by a decision node whose inputs are the values to compare, and which controls the (data flow) arrow between the parameter and the attribute in question.

This notation allows us to notate many things that can go wrong (or right) when scripts try to cooperate. Homogeneity of scripts means that when they control the same attribute, they utilize the same source (Figure 3). Inhomogeneity results from two processes that try to force the same attribute into conformance with conflicting parameters or policies (Figure 4).

  

Figure 5: Latent inhomogeneity masked by a single environmental side-effect.

  

Figure 6: Latent inhomogeneity hidden by multiple environmental side-effects.

It would seem from the above example that inhomogeneity is easy to observe and detect, but it can be easily masked and obscured by relatively common scripting errors so that it is only observable under specific environmental conditions.

For example, in Figure 5, script B changes an attribute P to a parameter value X depending upon conformance of a distinct attribute Q to a parameter Y. If another script C sets P according to another parameter rule Z, then the result of the sequence BC will always give P the value from Z, while the sequence CB will give P an inhomogeneous value only if Q is initially out of conformance with Y. Thus inhomogeneity of B and C is not observable except under certain (typically unknown) environmental preconditions.

One might think that this condition would be rare in traditional practice, but we actually find it very common in our own scripts! For example, we might want to update someone's password on a machine or network. This password is stored, with other information - such as the user's print name - that might be changed inadvertently at the same time as the password is changed.

Side-effects can make inhomogeneity arbitrarily difficult to detect. In Figure 6, three processes B, C, and D have homogeneous effects except when parameter W matches attribute R, parameter Y does not match attribute Q, and B and C are executed after script D. In this case alone, scripts B and C are inhomogeneous and the orders DBC and DCB will set attribute P according to conflicting parameters Z and X, respectively.

Thus inhomogeneity is very difficult to detect in general, even when the scripts being tested work properly in isolation and are fully convergent and aware of their effects. Using a generalization of the above construction, one can create a set of scripts for which every permutation produces the same result except within one particular environment, wherein two permutations produce inconsistent results.