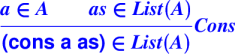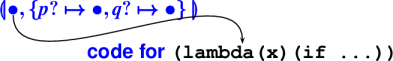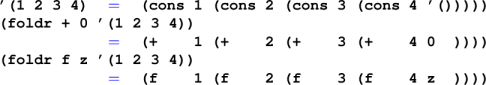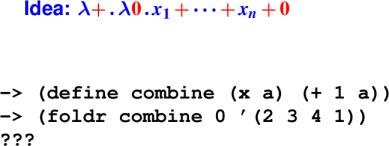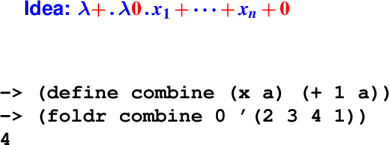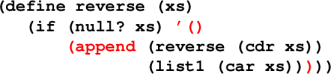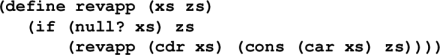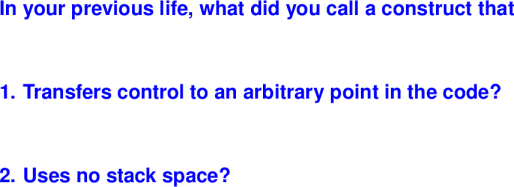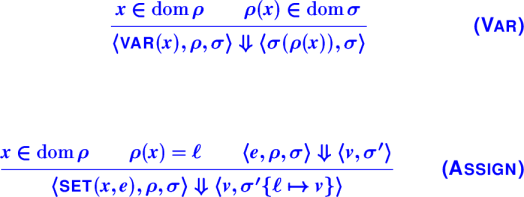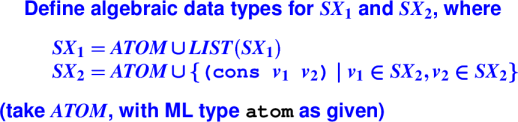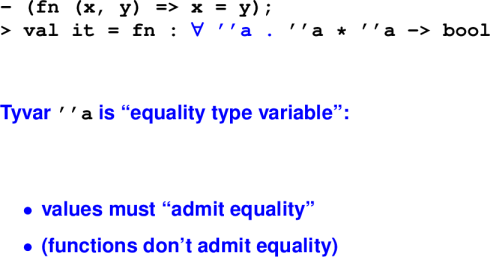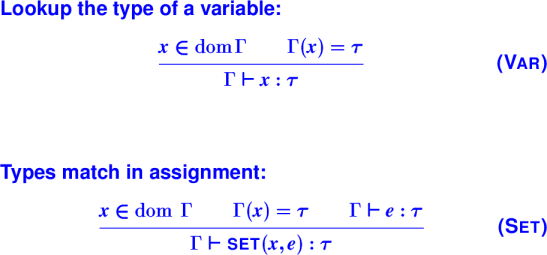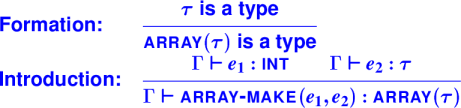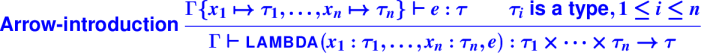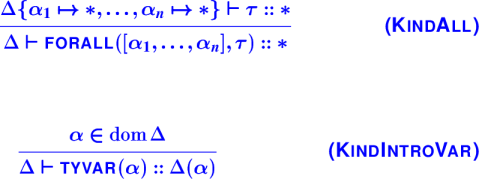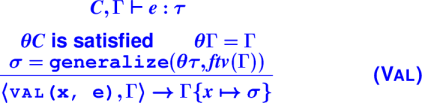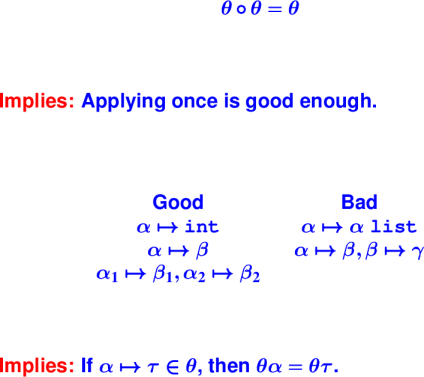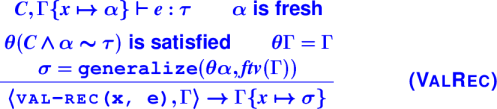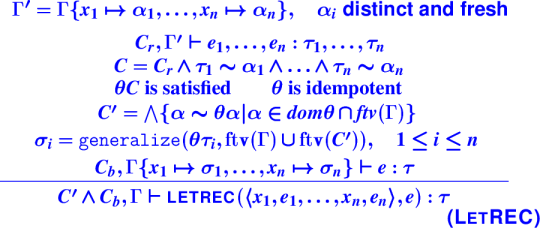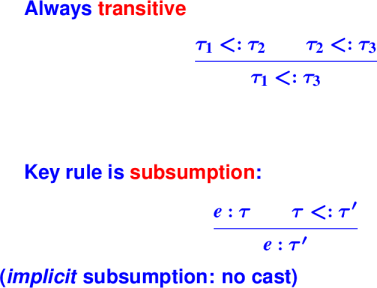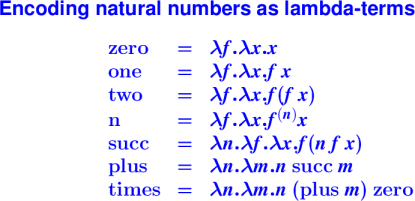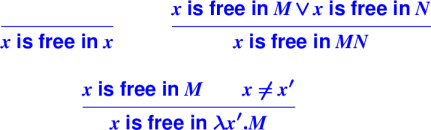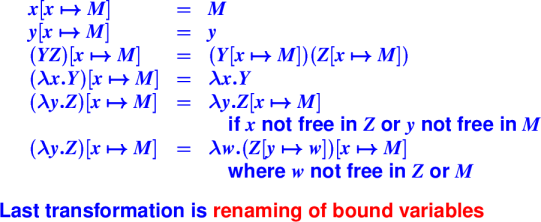Handout: 105 Tip Sheet
Topic of study: the stuff software is made of
- Thousands
- Each one unique
- Why do you suppose so many?
Conclusion: make it easier to write programs that really work
- An invaluable skill for software practitioners
Your language can make you or break you. - Compiler assignments at Princeton
Cultural enrichment: Paul Graham, especially the "Blub paradox"
- Java in January
- F# in February
- Modula-3 in March
- Ada in April
What if the course were called "Cooking"?
The same thing for programming languages:
Understanding core ideas of Programming Languages that manifest in many languages
The marriage of math and code
Principal tools: Induction and recursion
New ways of thinking about programming
Become a sophisticated consumer, aware of old wine in new bottles
Double your productivity
Bonus: preparation for advanced study
(Course has to serve everyone from fresh out of 15/61 to grad students)
If you're going to enjoy the course,
- You should enjoy programming (15)
- You should also like math (61, sort of---induction and proofs)
- You should be willing to work hard
Intellectual tools you need to understand, evaluate, and use languages effectively
Notations of the trade (source of precision, further study)
Learn by doing:
- Lots of short programs
- High power-to-weight ratio (lots of thought per line)
Just as intellectually challenging as COMP 40, but in an entirely different direction.
Language shapes your thinking
There aren't that many great features, and you will see them over and over
You'll choose features, and therefore languages, to fit your needs
Some are more powerful than others
In Comp 105,
Only the most powerful features need apply
We explode your brain so you can think differently
You'll know you're doing it right if at first your head hurts terribly, then you have a breakthrough moment and it all seems pleasant afterwards
To say more with less (expressive power):
- First-class functions
- Continuations
- Pattern matching
- Type inference
To promote reliability and reuse:
- Abstract data types
- Type polymorphism
- Objects and inheritance
- Modules and "generics"
Describing it all precisely:
- Operational semantics (daily tool of the trade)
- Denotational semantics (sheer beauty of the ideas, source of much code)
- Type rules (concise specifications of type systems)
You must get Norman's book (both volumes)
You won't need the book on ML for about a month
Homework will be frequent and challenging:
- Many small programming problems
- Some theory problems, more like a math problem set
- The occasional larger project, like a type checker or a game solver
- Submit electronically
- First homework is due a week from today; designed to get you moving quickly.
- The course is relentlessly cumulative.
Both individual and pair work:
- All problems should be discussed with others
(Essential to your success)
- Discussions must be acknowleged
- Most problems must be completed individually
- Do not allow anyone else to see your code
For some problems larger in scope, you will work in pairs
Be very careful to separate your pair work and your individual work. (A mistake could be major violation of academic integrity, with severe penalties.)
Arc of the homework looks something like this:
| impcore |
one star |
| opsem |
two stars |
| scheme |
three stars |
| hofs |
four stars |
And it's more or less four-star homeworks from there on out.
Lesson: don't make decisions based on the first couple of homeworks!
We don't cover everything in lecture
Lecture is for just the hard parts
We'll talk very little about the code (just the interesting bits)
In a 100-level course, you are responsible for your own learning
Course evaluations from previous years: a few students want everything gone over in lecture. That's not how things work in real life, and that's not how things work here. We point you in the right direction and identify traps and pitfalls, and we find good problems for you to work on.
If you're expecting to see everything in lecture, you have a couple of choices: change your expectations, or take the course next year when you will have more experience and will be more prepared to manage your own learning.
- Class goes very fast; recitations provide chance to dig in to key topics with classmates.
- Start this Thursday and Friday.
- Details on signing up on course web page.
- You are responsible!
- Treasure Hunt for participation points
Call me "Kathleen," "Professor Fisher", or "Profesor."
Goal: eliminate superficial differences
- Makes comparisons easy
- Differences that remain must be important!
Imperative programming with an IMPerative CORE:
Write a function that takes a natural number n and returns true (1) iff all the digits in n are 4's.
Code Note
Impcore variable definition
Example
(val n 99)
Compare
int n = 99;
Also, expressions at top level (definition of it)
Impcore expressions
No statements means expression-oriented:
(if e1 e2 e3)
(while e1 e2)
(set x e)
(begin e1 ... en)
(f e1 ... en)
Each one has a value and may have side effects!
Functions are primitive (+ - * / = < > print)
or defined with (define f ...).
The only type of data is "machine integer" (deliberate oversimplification)
Scopes also called "name spaces"; we will call them "environments" because that's the pointy-headed theory term---and if you want to read some of the exciting papers, pointy-headed theory has to be second nature.
Names known in "environments"
Ways to talk about meanings of names:
- Scope rules
- Name spaces
- Environments (aka symbol tables)
Impcore vars in 2 environments: globals, formals
There are no local variables
- Just like awk; if you need temps, use extra formal parameters
- For homework, you'll add local variables
Functions live in their own environment (not shared with variables)
Environmental abuse
Abuse of separate name spaces:
-> (val f 33)
33
-> (define f (x) (+ x x))
f
-> (f f)
66
Ways a recursive function could decompose a natural number n.
Peel back one (Peano numbers):
n = 0
n = m + 1, m is also a natural number
Split into two pieces:
n = 0
n = k + (n - k) 0 < k < n (everything gets smaller)
Sequence of decimal digits (see study problems on digits)
n = d, where 0 <= d < 10
n = 10 * m + d, where 0 <= d < 10 and m > 0
To do your homework problems, which I recommend starting today, you'll need to invent at least one more.
Question: How do we define the meaning of a program?
while (i < n && a[i] < x) { i++ }
Answer: Inductively
Atomic forms: Assign meaing directly (e.g., constants, variables)
Compound forms: Assign meaning using the meaning of the parts
Programming-languages people are wild about compositionality.
- Build sensible things from sensible pieces using just a few construction principles.
Example of compositionality: syntax (grammar)
Programming languages more orderly than natural language.
Example of non-compositionality
Question: What do we assign meaning to?
Answer: The Abstract Syntax Tree (AST) of the program.
Question: How can we represent all while loops?
while (i < n && a[i] < x) { i++ }
Answer:
Tag code as a while loop
Identify the condition, which can be any expression
Identify the body, which can be any expression
As a data structure:
WHILEX(exp1, exp2), where
exp1 = representation of (i < n && a[i] < x), and
exp2 = representation of i++
Norman Ramsey and Geoff Mainland put together some Beamer slides explaining operational semantics for Impcore.
Structure of the input drives the structure of the code.
To discover recursive functions, write algebraic laws:
sum 0 = 0
sum n = n + sum (n - 1)
Which direction gets smaller?
Code:
(define sum (n)
(if (= n 0) 0 (+ n (sum (- n 1)))))
Another example:
exp x 0 = 1
exp x (n + 1) = x * (exp x n)
Can you find a direction in which something gets smaller?
Code:
(define exp (x n)
(if (= n 0)
1
(* x (exp x (- n 1)))))
Programming with assignments etc
Recursion and composition:
Recursive function boot camp
Two recursive data structures: the list and the S-expression
More powerful ways of putting functions together (compositionality again, and it leads to reuse)
As a lens for understanding, you can ask these questions about any language:
What is the abstract syntax? What are the syntactic categories, and what are the terms in each category?
What are the values? What do expressions/terms evaluate to?
What environments are there? That is, what can names stand for?
How are terms evaluated? What are the judgments? What are the evaluation rules?
What's in the initial basis? Primitives and otherwise, what is built in?
Question 2: what are the values?
Two new kinds of data:
Picture of a cons cell: (cons 3 (cons ( 2 '())))
Values are S-expressions.
An S-expression is either
A list of S-expressions is either
Like any other abstract data type, S-Expresions have:
creators that create new values of the type '()
producers that make new values from existing values (cons s s')
mutators that change values of the type (not in uScheme)
observers that examine values of the type
number? symbol? boolean? null? car cdr
N.B. creators + producers = constructors
(cons 'a '()) also written '(a)
(cons 'b '(a))
(cons 'c '(b a))
(null? '(c b a)) equals #f
(cdr '(c b a) equals '(b a)
(car '(c b a) equals 'c
The symbol ' is pronounced "tick." It indicates that what follows is a literal.
What is the representation of
'((a b) (c d))
which can be alternatively written
cons( (cons a (cons b '())) cons( (cons c (cons d '())) '())
What is the representation of
cons('a 'b)
Contrast this representation with the one for
cons('a '())
Both of these expressions are S-expressions, but only cons('a '()) is a list.
Homework 1 grades have been mailed out. See Jerett or Jared if you have questions about grading.
Homework 2 is due tonight at midnight.
Homework 3 is available on the website. It is due Wed, Feb 17 at 6pm.
Can be defined via inference rules:

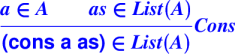
Constructors: '(),cons
Observers: null?, pair?, car, cdr (also known as "first" and "rest", "head" and "tail", and many other names)
Sequences a frequently used abstraction
Can easily approximate a set
Can implement finite maps with association lists (aka dictionaries)
You don't have to manage memory
These "cheap and cheerful" representations are less efficient than balanced search trees, but are very easy to implement and work with---see the book.
The only thing new here is automatic memory management. Everything else you could do in C. (You can have automatic memory management in C as well.)
Algebraic laws of lists:
(null? '()) == #t
(null? (cons v vs)) == #f
(car (cons v vs)) == v
(cdr (cons v vs)) == vs
Combine creators/producers with observers
Can use laws to prove properties of code and to write better code.
Any list is therefore constructed with '() or with cons applied to an atom and a smaller list.
- How can you tell the difference between these types of lists?
- What, therefore, is the structure of a function that consumes a list?
Example: length
Algebraic Laws for length
length '() = 0
length (cons x xs) = 1 + length xs
Code:
(define length (x)
(if (null? x)
0
(+ 1 (length (cdr x)))))
Using informal math notation with .. for "followed by" and e for the empty sequence, we have these laws:
xs .. e = xs
e .. ys = ys
(z .. zs) .. ys = z .. (zs .. ys)
xs .. (y .. ys) = (xs .. y) .. ys
The underlying operations are append, cons, and snoc. Which ..'s are which?
But we have no snoc
If we cross out the snoc law, we are left with three cases... but case analysis on the first argument is complete.
So cross out the law xs .. e == xs.
Which rules look useful for writing append?
*** Equations and function for append ***
(append '() ys) == ys
(append (cons z zs) ys) == (cons z (append zs ys))
(define append (xs ys)
(if (null? xs) ys
(cons (car xs) (append (cdr xs) ys))))
Why does it terminate?
The major cost center is cons because it corresponds to allocation.
How many cons cells are allocated?
Let's rigorously explore the cost of append.
IF
IH ('())
If a in A and IH(as) then IH (cons a as)
THEN
Forall as in List(A), IH(as)
Claim: Cost (append xs ys) = |xs|
Proof: By induction on the structure of xs.
Base case: xs = '()
(append '() ys) returns ys with 0 allocated cons cells.
Induction case: xs = (cons z zs)
car xs = z and cdr xs = zs and |xs| = 1 + |zs|
cost (append (cons z zs) ys)) =
cost (cons z (append zs ys)) =
1 + cost (append zs ys) =
By IH, cost (append zs ys) = |zs|
1 + |zs| =
|xs|
Conclusion: Cost of append is linear in length of first argument.
Algebraic laws for list reversal:
reverse '() = '()
reverse (x .. xs) = reverse xs .. reverse '(x) = reverse xs .. '(x)
And the code?
*** Naive list reversal ***
(define reverse (xs)
(if (null? xs) '()
(append (reverse (cdr xs))
(list1 (car xs)))))
The list1 function maps an atom x to the singleton list containing x.
How many cons cells are allocated? Let's let n = |xs|.
- Q: How many calls to
reverse? A: n
- Q: How many calls to
append? A: n
- Q: How long a list is passed to
reverse? A: n-1, n-2, ... , 0
- Q: How long a list is passed as first argument to
append? A: n-1, n-2, ... , 0
- Q: How many
cons cells are allocated by call to list1? A: one per call to reverse.
- Conclusion: O(n^2) cons cells allocated.
Let's try a new algebraic law:
reverse (x .. xs) .. zs = reverse xs .. x .. zs = reverse xs .. (cons x zs)
reverse '() .. zs = zs
The code
*** Reversal by accumulating parameters ***
(define revapp (xs zs)
(if (null? xs) zs
(revapp (cdr xs)
(cons (car xs) zs))))
(define reverse (xs) (revapp xs '()))
The cost of this version is linear in the length of the list being reversed.
Parameter zs is the accumulating parameter.
(A powerful, general technique.)
Implementation: list of key-value pairs
'((k1 v1) (k2 v2) ... (kn vn))
Picture with spine of cons cells, car, cdar, caar, cadar.
*** A-list example ***
-> (find 'Building
'((Course 105) (Building Braker)
(Instructor Fisher)))
Braker
-> (val ksf (bind 'Office 'Halligan-205
(bind 'Courses '(105)
(bind 'Email 'comp105-staff '()))))
((Email comp105-staff)
(Courses (105))
(Office Halligan-205))
-> (find 'Office ksf)
Halligan-205
-> (find 'Favorite-food ksf)
()
Notes:
- attribute can be a list or any other value
- 'nil' stands for 'not found'
*** Laws of assocation lists ***
(find k (bind k v l)) = v
(find k (bind k' v l)) = (find k l), provided k != k'
(find k '()) = '() --- bogus!
*** Introduce local names into environment ***
(let ((x1 e1)
...
(xn en))
e)
Evaluate e1 through en, bind answers to x1, ... xn
- Name intermediate results (simpler code, less error prone)
Creates new environment for local use only:
rho {x1 |-> v1, ..., xn |-> vn}
Also let* (one at a time) and letrec (local recursive functions)
Note that we really have definititions and it might be easier to read if McCarthy had actually used definition syntax, which you'll see in ML, Haskell, and other functional languages:
*** What McCarthy should have done ***
(let ((val x1 e1)
...
(val xn en))
e)
Things that should offend you about Impcore:
Look up function vs look up variable requires different interfaces!
To get a variable, must check 2 or 3 environments.
- Can't create a function without giving it a name:
- High cognitive overhead
- A sign of second-class citizenship
All these problems have one solution: lambda
From Church's lambda-calculus:
(lambda (x) (+ x x))
"The function that maps x to x plus x"
At top level, like define. (Or more accurately, define is a synonym for lambda that also gives the lambda a name.)
In general, \x.E or (lambda (x) E)
x is bound in E- other variables are free in
E
The ability to "capture" free variables is what makes it interesting.
(lambda (x) (+ x y)) ; means what??
What matters is that y can be a parameter or a let-bound variable of an enclosing function.
- Can tell at compile time what is captured.
- To understand why anyone cares, you'll need examples
First example: Finding roots. Given n and k, find an x such that x^n = k.
Step 1: Write a function that computes x^n - k.
Step 2: Write a function that finds a zero between lo and hi bounds.
Picture of zero-finding function. Algorithm uses binary search over integer interval between lo and hi. Finds point in that interval in which function is closest to zero.
Code that computes the function x^n - k given n and k:
*** Function escapes! ***
-> (define to-the-n-minus-k (n k)
(let
((x-to-the-n-minus-k (lambda (x)
(- (exp x n) k))))
x-to-the-n-minus-k))
-> (val x-cubed-minus-27 (to-the-n-minus-k 3 27))
-> (x-cubed-minus-27 2)
-19
The function to-the-n-minus-k is a higher-order function because it returns another (escaping) function as a result.
*** No need to name the escaping function ***
-> (define to-the-n-minus-k (n k)
(lambda (x) (- (exp x n) k)))
-> (val x-cubed-minus-27 (to-the-n-minus-k 3 27))
-> (x-cubed-minus-27 2)
-19
General purpose zero-finder that works for any function f:
*** The zero-finder ***
(define findzero-between (f lo hi)
; binary search
(if (>= (+ lo 1) hi)
hi
(let ((mid (/ (+ lo hi) 2)))
(if (< (f mid) 0)
(findzero-between f mid hi)
(findzero-between f lo mid)))))
(define findzero (f) (findzero-between f 0 100))
findzero-between is also a higher-order function because it takes another function as an argument. But nothing escapes; you can do this in C.
Example uses:
*** Cube root of 27 and square root of 16 ***
-> (findzero (to-the-n-minus-k 3 27))
3
-> (findzero (to-the-n-minus-k 2 16))
4
*** Lambda questions ***
(define combine (p? q?)
(lambda (x) (if (p? x) (q? x) #f)))
(define divvy (p? q?)
(lambda (x) (if (p? x) #t (q? x))))
(val c-p-e (combine prime? even?))
(val d-p-o (divvy prime? odd?))
(c-p-e 9) == ? (d-p-o 9) == ?
(c-p-e 8) == ? (d-p-o 8) == ?
(c-p-e 7) == ? (d-p-o 7) == ?
*** Lambda answers ***
(define conjoin (p? q?)
(lambda (x) (if (p? x) (q? x) #f)))
(define disjoin (p? q?)
(lambda (x) (if (p? x) #t (q? x))))
(val c-p-e (conjoin prime? even?))
(val d-p-o (disjoin prime? odd?))
(c-p-e 9) == #f (d-p-o 9) == #t
(c-p-e 8) == #f (d-p-o 8) == #f
(c-p-e 7) == #f (d-p-o 7) == #t
"Escape" means "outlive the function in which the lambda was evaluated."
We have already seen an example:
*** An ``escaping'' function ***
-> (define to-the-n-minus-k (n k)
(lambda (x) (- (exp x n) k)))
Where are n and k stored???
Picture of activation record for to-the-n-minus-k with n and k being popped.
Closures represent escaping functions:

An example:
*** What's the closure for conjunction? ***
(define conjoin (p? q?)
(lambda (x) (if (p? x) (q? x) #f)))
Closure for conjunction:
Preview: in math, what is the following equal to?
(f o g)(x) == ???
Another algebraic law, another function:
(f o g) (x) = f(g(x))
(f o g) = \x. (f (g (x)))
*** Functions create new functions ***
-> (define o (f g) (lambda (x) (f (g x))))
-> (define even? (n) (= 0 (mod n 2)))
-> (val odd? (o not even?))
-> (odd? 3)
-> (odd? 4)
Another example: (o not null?)
Currying converts a binary function f(x,y) to a function f' that takes x and returns a function f'' that takes y and returns the value f(x,y).
As we study higher-order functions in more detail, you will see why currying is useful.
*** Classic functional technique: Currying ***
-> (val positive? (lambda (y) (< 0 y)))
-> (positive? 3)
-> (val <-c (lambda (x) (lambda (y) (< x y))))
-> (val positive? (<-c 0)) ; "partial application"
-> (positive? 0)
Curried functions take their arguments "one-at-a-time."
*** What's the algebraic law for `curry`? ***
... (curry f) ... = ... f ...
Keep in mind:
All you can do with a function is apply it!
(((curry f) x) y) = f (x, y)
No need to Curry by hand!:

*** Exercises ***
-> (map ((curry +) 3) '(1 2 3 4 5))
???
-> (exists? ((curry =) 3) '(1 2 3 4 5))
???
-> (filter ((curry >) 3) '(1 2 3 4 5))
??? ; tricky
*** Answers ***
-> (map ((curry +) 3) '(1 2 3 4 5))
(4 5 6 7 8)
-> (exists? ((curry =) 3) '(1 2 3 4 5))
-> (filter ((curry >) 3) '(1 2 3 4 5))
(1 2)
*** Bonus content: vulnerable variables? ***
-> (val seed 1)
-> (val rand (lambda ()
(set seed (mod (+ (* seed 9) 5) 1024)))))
-> (rand)
14
-> (rand)
131
-> (set seed 1)
1
-> (rand)
14
Q: What's the problem with this approach?
A: The seed is exposed to the end user, who can break the abstraction of the rand function.
*** Bonus: Lambda as abstraction barrier! ***
-> (val mk-rand (lambda (seed)
(lambda ()
(set seed (mod (+ (* seed 9) 5) 1024))))))
-> (val rand (mk-rand 1))
-> (rand)
14
-> (rand)
131
-> (set seed 1)
error: set unbound variable seed
-> (rand)
160
Opsem grades have been mailed
Scheme homework due tonight at 6pm
HOFs homework due Sunday, Feb 28 at 11:59pm
Reasoning about Functions
Useful Higher-Order Functions
Tail Calls
Q: Can you do case analysis on a function?
A: No!
Q: So what can you do then?
A: Apply it!
Recursive function consuming A is related to proof about A
Q: How to prove two lists are equal?
A: Prove they are both '() or that they are both cons cells cons-ing equal car's to equal cdr's
Q: How to prove two functions equal?
A: Prove that when applied to equal arguments they produce equal results.
Goal: Start with functions on elements, end up with functions on lists
- Generalizes to sets, arrays, search trees, hash tables, ...
Goal: Capture common patterns of computation or algorithms
exists? (Ex: Is there a number?)all? (Ex: Is everything a number?)filter (Ex: Take only the numbers)map (Ex: Add 1 to every element)- foldr (General: can do all of the above.)
Fold also called reduce, accum, a "catamorphism"
Algorithm encapsulated: linear search
Example: Is there a even element in the list?
Algebraic laws:
(exists? p? '()) == ???
(exixts? p? '(cons a as)) == ???
(exists? p? '()) == #f
(exixts? p? '(cons a as)) == p? x or exists? p? xs
*** Defining exists? ***
-> (define exists? (p? xs)
(if (null? xs)
(if (p? (car xs))
(exists? p? (cdr xs)))))
-> (exists? pair? '(1 2 3))
-> (exists? pair? '(1 2 (3)))
-> (exists? ((curry =) 0) '(1 2 3))
-> (exists? ((curry =) 0) '(0 1 2 3))
Filter:

Algorithm encapsulated: Linear filtering
Example: Given a list of numbers, return only the even ones.
Algebraic laws:
(filter p? '()) == ???
(filter p? '(cons m ms)) == ???
(filter p? '()) == '()
(filter p? '(cons m ms)) == if (p? m)
(cons m (filter p? ms))
(filter p? ms)
*** Defining filter ***
-> (define filter (p? xs)
(if (null? xs)
'()
(if (p? (car xs))
(cons (car xs) (filter p? (cdr xs)))
(filter p? (cdr xs)))))
-> (filter (lambda (n) (> n 0)) '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter (lambda (n) (<= n 0)) '(1 2 -3 -4 5 6))
(-3 -4)
-> (filter ((curry <) 0) '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter ((curry >=) 0) '(1 2 -3 -4 5 6))
(-3 -4)
*** Composition Revisited: List Filtering ***
-> (val positive? ((curry <) 0))
<procedure>
-> (filter positive? '(1 2 -3 -4 5 6))
(1 2 5 6)
-> (filter (o not positive?) '(1 2 -3 -4 5 6))
(-3 -4)
Map:

Algorithm encapsulated: Transform every element
Example: Square every element of a list.
Algebraic laws:
(map f '()) == ???
(map f (cons n ns)) == ???
(map f '()) == '()
(map f (cons n ns)) == cons (f n) (map f ns)
*** Defining map ***
-> (define map (f xs)
(if (null? xs)
'()
(cons (f (car xs)) (map f (cdr xs)))))
-> (map number? '(3 a b (5 6)))
(#t #f #f #f)
-> (map ((curry *) 100) '(5 6 7))
(500 600 700)
-> (val square* ((curry map) (lambda (n) (* n n))))
<procedure>
-> (square* '(1 2 3 4 5))
(1 4 9 16 25)
Foldr:

Algebraic laws for foldr:

foldr takes two arguments:
Example: foldr plus zero '(a b)
cons a (cons b '())
| | |
v v v
plus a (plus b zero)
Code for foldr:

Another view of operator folding:
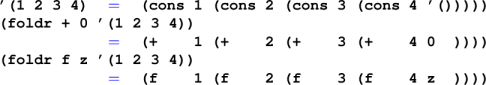
Exercise:
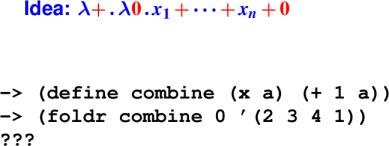
Wait for it:

Answer:
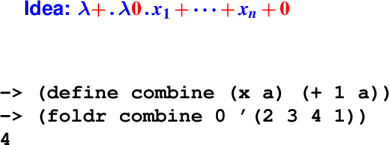
Intuition: In a function, a call is in tail position if it is the last thing the function will do.
A tail call is a call in tail position.
Important for optimizations: Can change complexity class.
What is tail position?
Tail position is defined inductively:
- The body of a function is in tail position
- When
(if e1 e2 e3) is in tail position, so are e2 and e3
- When
(let (...) e) is in tail position, so is e, and similary for letrec and let*.
- When
(begin e1 ... en) is in tail position, so is en.
Idea: The last thing that happens
Anything in tail position is the last thing executed!
Key idea is tail-call optimization!
Tail-call optimization:

Example of tail position:

Example of tail position:
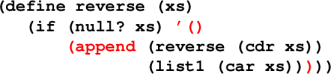
Example: reverse '(1 2)
Question: How much stack space is used by the call?
Call stack:
reverse '()
append
reverse '(2)
append
reverse '(1 2)
Answer: Linear in the length of the list
Another example of tail position:
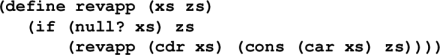
Another example of tail position:

Example: revapp '(1 2) '()
Question: How much stack space is used by the call?
Call stack: (each line replaces previous one)
revapp '(1 2) '() --> revapp '(2) '(1) --> revapp '() '(2 1)
Answer: Constant
Question:
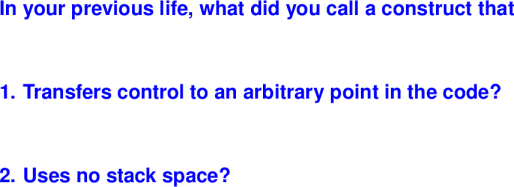
Answer: a goto!!
Think of "tail call" as "goto with arguments"
A continuation is code that represents "the rest of the computation."
- Not a normal function call because continuations never return
- Think "goto with arguments"
Direct style: Last action of a function is to return a value. (This style is what you are used to.)
Continuation-passing style (CPS): Last action of a function is to "throw" value to a continuation.
Compiler representation: Compilers for functional languages often convert direct-style user code to CPS because CPS matches control-flow of assembly.
Some languages provide a construct for capturing the current continuation and giving it a name k. Control can be resumed at captured continuation by throwing to k.
A style of coding that can mimic exceptions
Call-backs in GUI frameworks
How functions finish:

Design Problem: Missing Value:

Ideas?
Bad choices:
- nil
- special symbol
'fail
- run-time error
Good choice:
- exception (not in uScheme)
Solution: A New Interface:

*** Coding \lit{witness} with continuations ***
(define witness-cps (p? xs succ fail)
(if (null? xs)
(fail)
(let ((x (car xs)))
(if (p? x)
(succ x)
(witness-cps p? (cdr xs) succ fail)))))
``Continuation-Passing Style'':

Question: How much stack space is used by the call?
Answer: Constant
*** Example Use: Instructor Lookup ***
-> (val 2016s '((Fisher 105)(Hescott 170)(Chow 116)))
-> (instructor-info 'Fisher 2016s)
(Fisher teaches 105)
-> (instructor-info 'Chow 2016s)
(Chow teaches 116)
-> (instructor-info 'Souvaine 2016s)
(Souvaine is-not-on-the-list)
Instructor Lookup: The Code:

Instructor Lookup: The Code:

Instructor Lookup: The Code:
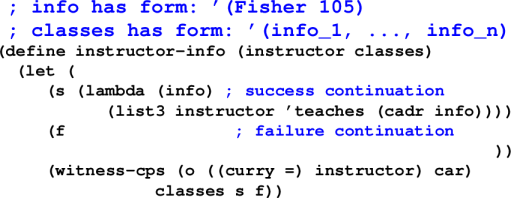
Instructor Lookup: The Code:

*** Exercise: Find a satisfying assignment if one exists ***
(val f1 '(and x y z w p q (not x)))
(val f2 '(not (or x y)))
(val f3 '(not (and x y z)))
(val f4 '(and (or x y z)
(or (not x) (not y) (not z))))
Wait for it ...:

*** Satisfying assignments ***
(val f1 '(and x y z w p q (not x))) ; NONE
(val f2 '(not (or x y)))
; { x |-> #f, y |-> #f }
(val f3 '(not (and x y z)))
; { x |-> #f, ... }
(val f4 '(and (or x y z)
(or (not x) (not y) (not z))))
; { x |-> #f, y |-> #t, ... }
Continuations for Search:

start carries a partial truth assignment to variables current
Box describes how to extend current to make a variable, say x, true.
Case 1: current(x) = #t
Call success continuation with current
Pass fail as resume continuation (argument to success)
Case 2: current(x) = #f
Call fail continuation
Case 3: x not in current
Call success cotinuation with current{x -> #t}
Pass fail as resume continuation
start carries a partial truth assignment to variables current
Box describes how to extend current to make a negated variable, say not x, true.
Case 1: current(x) = #f
Call success continuation with current
Pass fail as resume continuation (argument to success)
Case 2: current(x) = #t
Call fail continuation
Case 3: x not in current
Call success cotinuation with current{x -> #f}
Pass fail as resume continuation
Solver enters A
If A is solved, newly allocated success continuation starts B
If B succeeds, we're done! Use success continuation from context.
If B fails, use resume continuation A passed to B as fail.
If A fails, the whole thing fails. Use fail continuation from context.
Solver enters A
If A is solved, we're good! But what if context doesn't like solution? It can resume A using the resume continuation passed out as fail.
If A can't be solved, don't give up! Try a newly allocated failure continuation to start B.
If ever B is started, we've given up on A entirely. So B's success and failure continuations are exactly the ones in the context.
If B succeeds, but the context doesn't like the answer, the context can resume B.
If B fails, abject failure all around; call the original fail continuation.
Scheme grades have been mailed
HOFs homework due Sunday, Feb 28 at 11:59pm
Scheme Semantics
Scheme as it really is
First four of five questions: Syntax, Values, Environments, Evaluation
Key changes from Impcore:
New constructs: let, lambda, application (not just names)
New values: cons cells and functions (closures)
A single environment
{New Abstract Syntax}:

{New Evaluation Judgment}:

It's not precisely true that rho never changes.
New variables are added when they come into scope.
Old variables are deleted when they go out of scope.
But the location associated with a variable never changes.
The book includes all rules for uScheme. Here we will discuss on key rules.
{New Evaluation Rules}:
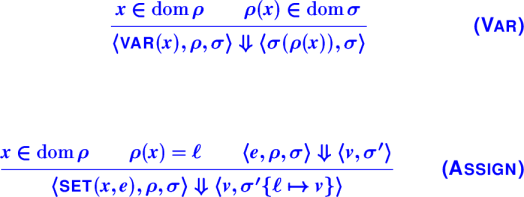
Board: Picture of environment pointing to store.
Questions about Assign:
What changes are captured in σʹ?
What changes are captured in σʹ{ℓ ↦ v}?
What would happen if we used σ instead of σʹ
What would happen if we used a fresh ℓ?
Some other ℓ in the range of ρ?
{Semantics of Lambda}:

{Applying Closures}:

Questions about ApplyClosure:
What if we used σ instead of σ0 in evaluation of e1?
What if we used σ instead of σ0 in evaluation of arguments?
What if we used ρc instead of ρ in evaluation of arguments?
What if we did not require ℓ1, …, ℓn ∉ dom(σ)?
What is the relationship between ρ and σ?
{Locations in Closures}:

Picture of environment and store that results from executing above program.
Closure Optimizations
- Major issue in making functional programs efficient
- Keep closures on the stack
- Share closures
- Eliminate closures (when functions don't escape)
Midterm: Wednesday, March 2, in-class. You may bring one-page of notes.
Monday's Class: Midterm Review. Bring Questions! In-class evaluations.
Scheme Wrap-up
Intro to ML
{uscheme and the Five Questions}:

Advantages:
- High-level data structures
- Cheap, easy recursion
- Automatic memory management (garbage collection!)
- Programs as data!
- Hygenic macros for extending the language
- Big environments, tiny interpreters, everything between
- Sophisticated Interactive Development Environments
- Used in AI applications; ITA; Paul Graham's company Viaweb
Down sides:
- Hard to talk about data
- Hard to detect errors at compile time
Bottom line: it's all about lambda
- Major win
- Real implementation cost (heap allocation)
- Macros!
- Cond expressions (solve nesting problem)
- Mutation
- ...
Real Scheme: Macros
A Scheme program is just another S-expression
Function define-syntax manipulates syntax at compile time
Macros are hygienic---name clashes impossible
let, and, many others implemented as macros
*** Real Scheme: Conditionals ***
(cond (c1 e1) ; if c1 then e1
(c2 e2) ; else if c2 then e2
... ...
(cn en)) ; else if cn then en
; Syntactic sugar---'if' is a macro:
(if e1 e2 e3) == (cond (e1 e2)
(#t e3))
Real Scheme: Mutation
Not only variables can be mutated.
Mutate heap-allocated cons cell:
(set-car! '(a b c) 'd) => (d b c)
Circular lists, sharing, avoids allocation
- still for specialists only
Apply your new knowledge in Standard ML:
- You've already learned (most of) the ideas
- There will be a lot of new detail
- Good language for implementing language features
- Good language for studying type systems
Lectures on ML:
- Algebraic types and pattern matching
- Exceptions
- An introduction to types
Meta: Not your typical introduction to a new language
- Not definition before use, as in a manual
- Not tutorial, as in Ullman
- Instead, the most important ideas that are most connected to your work up to now
Designed for programs, logic, symbolic data
Theme: Precise ways to describe data
ML = uScheme + pattern matching + exceptions + static types
uScheme
(cons x xs)
'()
(lambda (x) e)
or and
#t #f
(let (x e1) e2)
ML
x :: xs
[] or nil
fn x => e
orelse andalso
true false
let val x = e1 in e2 end
- Pattern matching is big and important. You will like it.
- Exceptions are easy
- Static types get two to three weeks in their own right.
Pattern matching facilitates case analysis.
Static types tell us at compile time what the cases are.
And lots of new concrete syntax!
The length function.
Algebraic laws:
length [] = 0
length (x::xs) = 1 + length xs
The code:
fun length [] = 0
| length (x::xs) = 1 + length xs
Things to notice:
No brackets! (I hate the damn parentheses)
Function application by juxtaposition
Function application has higher precedence than any infix operator
Compiler checks all the cases (try in the interpreter)
Let's try another! map, filter, exists, all, take, drop, takewhile, dropwhile
*** Length ***
fun length [] = 0
| length (x::xs) = 1 + length xs
val res = length [1,2,3]
*** Map ***
fun map f [] = []
| map f (x::xs) = (f x) :: (map f xs)
val res1 = map length [[], [1], [1,2], [1,2,3]]
*** Filter ***
fun filter pred [] = []
| filter pred (x::xs) =
let val rest = filter pred xs in
if pred x
then (x::rest)
else rest
end
val res2 = filter (fn x => (x mod 2) = 0) [1,2,3,4]
(* Note: the convention of using a question mark in the
names of predicates doesn't work in SML. *)
*** Exists ***
fun exists pred [] = false
| exists pred (x::xs) =
(pred x) orelse (exists pred xs)
val res3 = exists (fn x => (x mod 2) = 1) [1,2,3,4]
(* Note fn x => e is syntax for lambda in SML *)
*** All ***
fun all pred [] = true
| all pred (x::xs) =
(pred x) andalso (all pred xs)
val res4 = all (fn x => (x >= 0)) [1,2,3,4]
*** Take ***
exception ListTooShort
fun take 0 l = []
| take n [] = raise ListTooShort
| take n (x::xs) = x::(take (n-1) xs)
val res5 = take 2 [1,2,3,4]
val res6 = take 3 [1] handle ListTooShort => (print "List too short!"; [])
(* Note use of exceptions. *)
*** Drop ***
fun drop 0 l = l
| drop n [] = raise ListTooShort
| drop n (x::xs) = (drop (n-1) xs)
val res7 = drop 2 [1,2,3,4]
val res8 = drop 3 [1] handle ListTooShort => (print "List too short!"; [])
*** Takewhile ***
fun takewhile p [] = []
| takewhile p (x::xs) =
if p x then (x::(takewhile p xs)) else []
fun even x = (x mod 2 = 0)
val res8 = takewhile even [2,4,5,7]
val res9 = takewhile even [3,4,6,8]
*** Drop while ***
fun dropwhile p [] = []
| dropwhile p (a as (x::xs)) =
if p x then (dropwhile p xs) else a
val res10 = dropwhile even [2,4,5,7]
val res11 = dropwhile even [3,4,6,8]
(* fancy pattern form: a as (x::xs) *
*** Fold ***
fun foldr p zero [] = zero
| foldr p zero (x::xs) = p (x, (foldr p zero xs))
fun foldl p zero [] = zero
| foldl p zero (x::xs) = foldl p (p (x, zero)) xs
val res12 = foldr (op +) 0 [1,2,3,4]
val res13 = foldl (op * ) 1 [1,2,3,4]
(* Note op to convert an infix operator into a function *)
ML---The Five Questions
Syntax: definitions, expressions, patterns, types
Values: num/string/bool, record/tuple, algebraic data
Environments: names stand for values (and types)
Evaluation: uScheme + case and pattern matching
Initial Basis: medium size; emphasizes lists
(Question Six: type system---a coming attraction)
A note about books
Ullman is easy to digest
Ullman is clueless about good style
Suggestion:
- Learn the syntax from Ullman
- Learn style from Ramsey
Tidbits:
The most important idea in ML!
Originated with Hope (Burstall, MacQueen, Sannella), in the same lab as ML, at the same time (Edinburgh!)
Board:
A "suit" is produced using hearts, diamonds, clubs, or spades
A "list of A" is produced using nil or a :: as, where a is an A and as is a "list of A"
A "heap of A" is either empty or it's an A and two child heaps
*** Datatype declarations ***
datatype suit = hearts | diamonds | clubs | spades
datatype 'a list = nil (* copy me NOT! *)
| op :: of 'a * 'a list
datatype 'a heap = EHEAP
| HEAP of 'a * 'a heap * 'a heap
type suit val hearts : suit, ...
type 'a list val nil : forall 'a . 'a list
val op :: : forall 'a .
'a * 'a list -> 'a list
type 'a heap
val EHEAP: forall 'a. 'a heap
val HEAP : forall 'a.'a * 'a heap * 'a heap -> 'a heap
Exegesis (on board):
Notation 'a is a type variable
- On left-hand side, it is a formal type parameter
- On right-hand side it is an ordinary type
- In both cases it represents a single unknown type
Name before = introduces a new type constructor into the type environment. Type constructors may be nullary.
Alternatives separated by bars are value constructors of the type
They are new and hide previous names
(Do not hide built-in names nil and list from the initial basis!)
Value constructors participate in pattern matching
Complete by themselves: hearts, spades, nil
Expect parameters to make a value or pattern: ::, HEAP
op enables an infix operator to appear in a nonfix context
Type application is postfix
- A list of integer lists is written:
int list list
New names into two environments:
suit, list, heap stand for new type constructors
hearts, clubs, nil, ::, EHEAP, HEAP stand for new value constructors
Algebraic datatypes are inherently inductive (list appears in its own definition)---to you, that means finite trees
'a * 'a list is a pair type --- infix operators are always applied to pairs
Recitation-leader Midterm Review: 7-9pm Monday, Halligan 102
Midterm: Wednesday in class; 1-page self-prepared sheet of notes
Midterm review
Sample Problems
Course Evaluations
Plan on:
Recursion and Induction
Write recursive functions
- Explain why function terminates
Prove properties using induction
- Explain why induction is well-founded
Algebraic laws can lead naturally to recursive functions and inductive proofs
Understanding a language: Key Questions
What is the abstract syntax?
What are the values?
What are the environments?
How does evaluation happen?
What is the initial basis?
What are the types?
First-class functions
What they are
How to use them effectively
Lambdas create anonymous functions
Closures are run-time representation of functions; they capture the environment at closure-definition time
Continuations capture the rest of the computation
Local bindings
Various forms: let, let*, and letrec
What is let used for?
How do the various forms differ?
Data structures and associated operations
S-expressions ((), null?, cons, car, cdr, ...)
Lists
Tuples
Cost Models and Optimizations
Operational semantics
Precisely describe meaning of programs
Written using inference rules
Judgement forms capture all relevant information
Environments track information about variables
Stores map locations to values
Datatypes can define an enumerated type and associated values.
datatype suit = heart | diamond | spade | club
Here suit is the name of a new type.
The data constructors heart, dimaond, spade, and club are the values of type suit.
Data constructors are separated by vertical bars.
Datatypes are deconstructed using pattern matching.
fun toString heart = "heart"
| toString diamond = "diamond"
| toString spade = "spade"
| toString club = "club"
val suitName = toString heart
datatype IntTree = Leaf | Node of int * IntTree * IntTree
IntTree is the name of a new type.
There are two data constructors: Leaf and Node.
Nodes take a tuple of three arguments: a value at the node, and left and right subtrees.
The keyword of separates the name of the data constructor and the type of its argument.
When fully applied, data constructors have the type of the defining datatype (ie, IntTree).
We build values of type IntTree using the associated constructors: (Draw on board)
val tempty = Leaf
val t1 = Node (1, tempty, tempty)
val t2 = Node (2, t1, t1)
val t3 = Node (3, t2, t2)
What is the in-order traversal of t3?
[1,2,1,3,1,2,1]
What is the pre-order traversal of t3?
[3,2,1,1,2,1,1]
(The @ symbol denotes append in ML)
fun inOrder Leaf = []
| inOrder (Node (v, left, right)) =
(inOrder left) @ [v] @ (inOrder right)
val il3 = inOrder t3
fun preOrder Leaf = []
| preOrder (Node (v, left, right)) =
v :: (preOrder left) @ (preOrder right)
val pl3 = inOrder t3
IntTree is monomorphic because it has a single type.
Note though that the inOrder and preOrder functions only cared about the structure of the tree, not the payload value at each node.
Polymorphic datatypes are written using type variables that can be instantiated with any type.
datatype 'a tree = Child | Parent of 'a * 'a tree * 'a tree
tree is a type constructor (written in post-fix notation), which means it produces a type when applied to a type argument.
Examples:
int tree is a tree of integers
bool tree is a tree of booleans
char tree is a tree of characters
int list tree is a tree of a list of integers.
'a is a type variable: it can represent any type.
It is introduced on the left-hand of the = sign. References on the right-hand side are types.
Child and Parent are data constructors.
Child takes no arguments, and so has type 'a tree
When given a value of type 'a and two 'a trees, Parent produces a 'a tree
val empty = Child
val tint1 = Parent (1, empty, empty)
val tint2 = Parent (2, tint1, tint1)
val tint3 = Parent (3, tint2, tint2)
val tstr1 = Parent ("a", empty, empty)
val tstr2 = Parent ("b", tstr1, tstr1)
val tstr3 = Parent ("c", tstr2, tstr2)
fun inOrder Child = []
| inOrder (Parent (v, left, right)) =
(inOrder left) @ [v] @ (inOrder right)
fun preOrder Child = []
| preOrder (Parent (v, left, right)) =
v :: (preOrder left) @ (preOrder right)
Functions inOrder and preOrder are polymorphic: they work on any value of type 'a tree. 'a is a type variable and can be replaced with any type.
Datatype declarations introduce names into:
the type environment: suit, IntTree, tree
the value environment: heart, Leaf, Parent
Datatype declarations are inherently inductive:
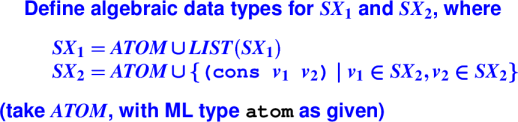
Wait for it ...
*** Exercise answers ***
datatype sx1 = ATOM1 of atom
| LIST1 of sx1 list
datatype sx2 = ATOM2 of atom
| PAIR2 of sx2 * sx2
Eliminate values of algebraic types
New language construct case (an expression)
fun length xs =
case xs
of [] => 0
| (x::xs) => 1 + length xs
At top level, fun better than case
When possible, write
fun length [] = 0
| length (x::xs) = 1 + length xs
case works for any datatype
fun toStr t =
case t
of Leaf => "Leaf"
| Node(v,left,right) => "Node"
But often pattern matching is better style:
fun toStr' Leaf = "Leaf"
| toStr' (Node (v,left,right)) = "Node"
Part of learning any new field: talk to people in their native vocabulary
Introduce means "produce", "create", "make", "define"
Eliminate means "consume", "examine", "observe", "use"
It's like knowing what to say when somebody sneezes.
Types and their uses:
|
Type
|
Produce
|
Consume
|
|
Introduce
|
Eliminate
|
|
arrow (function)
|
Function definition or Lambda (fn)
|
Application
|
|
algebraic datatype
|
Apply constructor
|
Case or Pattern match
|
|
tuple
|
(e1, ..., en)
|
Case or Pattern match!
|
val (x,y) = (1,2)
val (left, pivot, right) = split xs
val (n,xs) = (3, [1,2,3])
val (x::xs) = [1,2,3]
val (_::xs) = [1,2,3]
- Declaration:
exception EmptyQueue
- Introduction:
raise e where e : exn
- Elimination:
e1 handle pat => e2
ML Traps and pitfalls:

*** Order of clauses matters ***
fun take n (x::xs) = x :: take (n-1) xs
| take 0 xs = []
| take n [] = []
(* what goes wrong? *)
*** Gotcha --- overloading ***
- fun plus x y = x + y;
> val plus = fn : int -> int -> int
- fun plus x y = x + y : real;
> val plus = fn : real -> real -> real
Gotcha --- equality types:
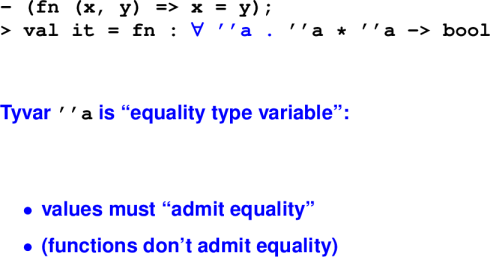
Gotcha --- parentheses
Put parentheses around anything with |
case, handle, fn
Function application has higher precedence than any infix operator
*** Syntactic sugar for lists ***
- 1 :: 2 :: 3 :: 4 :: nil; (* :: associates to the right *)
> val it = [1, 2, 3, 4] : int list
- "the" :: "ML" :: "follies" :: [];
> val it = ["the", "ML", "follies"] : string list
> concat it;
val it = "theMLfollies" : string
ML from 10,000 feet:

The value environment
Names bound to immutable values
Immutable ref and array values point to mutable locations
ML has no binding-changing assignment
Definitions add new bindings (hide old ones):
val pattern = exp
val rec pattern = exp
fun ident patterns = exp
datatype ... = ...
Nesting environments
At top level, definitions
Definitions contain expressions:
def ::= val pattern = exp
Expressions contain definitions:
exp ::= let defs in exp end
Sequence of defs has let-star semantics
What is a pattern?
pattern ::= variable
| wildcard
| value-constructor [pattern]
| tuple-pattern
| record-pattern
| integer-literal
| list-pattern
Design bug: no lexical distinction between
- VALUE CONSTRUCTORS
- variables
Workaround: programming convention
Function pecularities: 1 argument
Each function takes 1 argument, returns 1 result
For "multiple arguments," use tuples!
fun factorial n =
let fun f (i, prod) =
if i > n then prod else f (i+1, i*prod)
in f (1, 1)
end
fun factorial n = (* you can also Curry *)
let fun f i prod =
if i > n then prod else f (i+1) (i*prod)
in f 1 1
end
Tuples are "usual and customary."
Mutual recursion:

Syntax of ML types:

Syntax of ML types:

Polymorphic types:

Old and new friends:
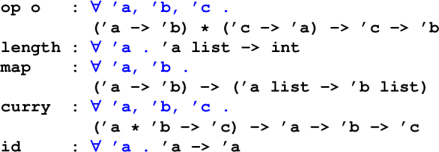
What kind of value do we have?
Type systems classify values.
n + 1
"hello" ^ "world"
(fn n => n * (n - 1))
if p then 1 else 0
Questions type systems can answer:
What kind of value does it evaluate to (if it terminates)?
What is the contract of the function (!)
Does this program contain certain kinds of errors?
Who has the rights to look at it/change it?
Is the number miles or millimeters?
Questions type systems generally cannot answer:
Will my program contain a division by zero?
Will my program contain an array bounds error?
Will my program take the car of `'()?
Will my program terminate?
Suppose L is a Turing-Complete Language.
TP is the set of programs in L that terminate.
Wish: a type system to statically classify terminating programs:
Expression e in L has type T (e : T) iff e terminates.
But: Undecideable!
We can prove no such type system exists.
Choices:
Most languages use a combination of static and dynamic checks
Static:
input independent
efficient at run-time
approximate
Dynamic:
depends on input
run-time overhead
precise
As a working definition, a set of values
As a precise definition, a classifier for terms!!
- Note: a computation can have a type even if it never produces a value!
Source of new language ideas for next 20 years
Needed if you want to understand advanced designs (or create your own)
Define an AST for expressions with:
- Simple integer arithmetic operations
- Numeric comparisons
- Conditional
- Numeric literal
Language of expressions
Numbers and Booleans:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| LIT of int
| IF of exp * exp * exp
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = INTTY | BOOLTY
Can't add an integer and a boolean:
3 + (3 < 99)
(ARITH(PLUS, LIT 3, CMP (LT, LIT 3, LIT 99)))
Can't compare an integer and a boolean
(3 < (4 = 24))
CMP (LT, LIT 3, CMP(EQ (LIT 4, LIT 24)))
Form of judgment Context |- term : type
Written |- e : tau
Contexts vary between type systems
(Right now, the empty context)
Inference rules determine how to code val tc : exp -> ty:
Given e, find tau such that |- e : tau
What inference rules do you recommend for this language?
Informal example:
|- 3 : int |- 5 : int
------------------------------------------------------------
|- 3 + 5 : int
General form:
|- e1 : int |- e2 : int
------------------------------------------------------------
|- ARITH ( _ , e1, e2) : int
Informal example:
|- 7 : int |- 10 : int
------------------------------------------------------------
|- 7 < 10 : bool
General form:
|- e1 : int |- e2 : int
------------------------------------------------------------
|- CMP ( _ , e1, e2) : bool
Informal example:
|- 14 : int
General form:
-----------------------------------
|- LIT (n) : int
Informal example:
|- true : bool
|- 3 : int
|- 42 : int
------------------------------------------------------------
|- IF (true, 3, 42) : int
General form:
|- e : bool
|- e1 : tau1
|- e2 : tau2 tau1 equiv tau2
------------------------------------------------------------
|- IF ( e, e1, e2) : tau1
Experience shows it is better to test two types for equivalence than to write rule with same type appearing twice.
Typing rules let us read off what a type checker needs to do.
input to checker: e
output from checker: tau
val tc : exp -> ty
exception IllTyped
fun tc (ARITH (_, e1, e2)) =
case (tc e1, tc e2)
of (INTTY, INTTY) => INTTY
| _ => raise IllTyped
| tc (CMP (_, e1, e2)) =
case (tc e1, tc e2)
of (INTTY, INTTY) => BOOLTY
| _ => raise IllTyped
| tc (LIT _) = INTTY
| tc (IF (e,e1,e2)) =
case (tc e, tc e1, tc e2)
of (BOOLTY, tau1, tau2) =>
if eqType(tau1, tau2)
then tau1 else raise IllTyped
| _ => raise IllTyped
An implementor's trick: If you see identical types in a rule,
Give each type a distinct subscript
Introduce equality constraints
Remember to be careful using primitive equality to check types---you are better off with eqType.
Add variables and let binding to our language, what happens?
Extended language of expressions
Numbers and Booleans:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| LIT of int
| IF of exp * exp * exp
| VAR of name
| LET of name * exp * exp
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = INTTY | BOOLTY
What could go wrong with a variable?
Used inconsistently:
;; x can't be both an integer and a list
x + x @ x
;; y can't be both an integer and a string
let y = 10 in y ^ "hello" end
Need to track variable use to ensure consistency
Key idea: Type environment (Gamma) tracks the types of variables.
x in domain Gamma tau = Gamma(x)
------------------------------------------------------------
Gamma |- VAR x : tau
Gamma |- e : tau
Gamma{x->tau} |- e' : tau'
------------------------------------------------------------
Gamma |- LET x = e in e' : tau'
Type checker needs Gamma -- gives type of each "term variable".
val tc : ty env -> exp -> ty
fun tc Gamma (ARITH ... ) = <as before>
| tc Gamma (VAR x) =
case Gamma (x)
of Some tau => tau
| None => raise IllTyped
| tc Gamma (LET x, e1, e2) =
let tau1 = tc Gamma e1
in tc (extend Gamma x tau1) e2
end
Introduction:
Gamma{x->tau1} |- e : tau2
------------------------------------------------------------
Gamma |- fn x : tau1 => e : tau1 -> tau2
Elimination:
Gamma |- e : tau1 -> tau2
Gamma |- e1 : tau1
------------------------------------------------------------
Gamma |- e e1 : tau2
Review
I gave you syntax for simple language
You came up with typing rules
I showed you how to implement the type checker.
Then on your homework,
You will design new syntax and typing rules for lists
You will extend an existing type checker
You will implement a full type checker from scratch
This is a big chunk of what language designers do.
Type checking with type constructors
Formation, Introduction, and Elimination Rules
New watershed in the homework
You've been developing and polishing programming skills: recursion, higher-order functions, using types to your advantage. But the problems have been mostly simple problems around simple data structures, mostly lists.
We're now going to shift and spend the next several weeks doing real programming-languages stuff, starting with type systems.
You've already seen everything you need to know to implement a basic type checker, and you are almost fully equipped to add array operations and types to Typed Impcore.
What's next is much more sophisticated type systems, with an infinite number of types. We'll focus on two questions:
What is and is not a good type, that is, a classifier for terms?
How shall we represent types?
We'll look at these questions in two contexts: monomorphic and polymorphic languages.
Monomorphic types have "one shape."
- Examples:
int, bool, int -> bool, int * int
Polymorphic types have "many shapes."
- Examples:
'a list, 'a list -> 'a list, ('a * int)
Language designer's agenda:
What new types do I have (formation rules)?
What new syntax do I have to create terms of a type (introduction rules)?
What new syntax do I have to observe terms of a type (elimination rules)?
Here's how it works:
Every new variety of type requires special syntax
We get three kinds of typing rules: formation, introduction, and elimination
Implementation is a straightforward application of what you already know.
Question: If I add lists to a language, how many new types am I introducing?
Type rules for variables:
Type rules for control:

Notice: one rule for if!!
Product types: Both x and y:

(At run time, identical to cons, car, cdr)
Arrow types: Function from x to y:

Arrow types: Function from x to y:

Typical syntactic support for types
Explicit types on lambda and define:
For lambda, argument types:
(lambda ((int n) (int m)) (+ (* n n) (* m m)))
For define, argument and result types:
(define int max ((int x) (int y)) (if (< x y) y x))
Abstract syntax:
datatype exp = ...
| LAMBDA of (name * tyex) list * exp
...
datatype def = ...
| DEFINE of name * tyex * ((name * tyex) list * exp)
...
Array types: Array of x:
Array types continued:

References (similar to C/C++ pointers):

Wait for it ...
Reference Types:

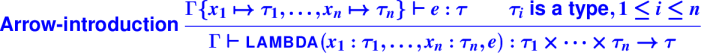
*** Type-checking LAMBDA ***
datatype exp = LAMBDA of (name * tyex) list * exp
...
fun ty (Gamma, LAMBDA (formals, body)) =
let val Gamma' = (* body gets new env *)
foldl (fn ((n, ty), g) => bind (n, ty, g))
Gamma formals
val bodytype = ty(Gamma', body)
val formaltypes =
map (fn (n, ty) => ty) formals
in funtype (formaltypes, bodytype)
end
Type System homework due Tuesday, March 29.
Monday: Typed Impcore
Today: TypedUScheme
Type formation: Composing types
Typed Impcore:
Standard ML:
Can't add new syntactic forms and new type formation rules for every new type.
Representing type constructors generically:

Question: How would you represent an array of pairs of booleans?:

Question: How would you represent an array of pairs of booleans?:

Well-formed types
We still need to classify type expressions into:
types that classify terms (eg, int)
type constructors that build types (eg, list)
nonsense terms that don't mean anything (eg, int int)
Idea:
We use types to classify expressions.
Apply the same idea to classify types.
Kinds are to types as types are to expressions.
Monomorphic types are limiting
Each new type constructor requires
- Special syntax
- New type rules
- New internal representation (type formation)
- New code in type checker (intro, elim)
- Do another proof of soundness
Monomorphism hurts programmers too
Monomorphism leads to code duplication
User-defined functions are monomorphic:
(define int lengthI ((list int) l)
(if (null? l) 0 (+ 1 (lengthI (cdr l)))))
(define int lengthB ((list bool) l)
(if (null? l) 0 (+ 1 (lengthB (cdr l)))))
(define int lengthS ((list sym) l)
(if (null? l) 0 (+ 1 (lengthS (cdr l)))))
Quantified types:

Representing quantified types
Two new alternatives for tyex:
datatype tyex
= TYCON of name
| CONAPP of tyex * tyex list
| FORALL of name list * tyex
| TYVAR of name
Kinding rules for quantified types:
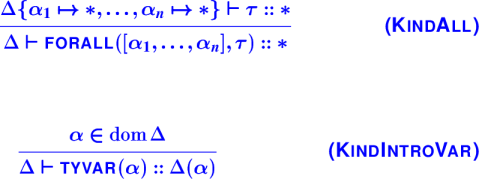
*** Programming with these types ***
Substitute for quantified variables
-> length
<proc> : (forall ('a) (function ((list 'a)) int))
-> (@ length int)
<proc> : (function ((list int)) int)
-> (length '(1 2 3))
type error: function is polymorphic; instantiate before applying
-> ((@ length int) '(1 2 3))
3 : int
*** Substitute what you like ***
-> length
<proc> : (forall ('a) (function ((list 'a)) int))
-> (@ length bool)
<proc> : (function ((list bool)) int)
-> ((@ length bool) '(#t #f))
2 : int
*** More ``Instantiations'' ***
-> (val length-int (@ length int))
length-int : ((list int) -> int)
-> (val cons-bool (@ cons bool))
cons-bool : ((bool (list bool)) ->
(list bool))
-> (val cdr-sym (@ cdr sym))
cdr-sym : ((list sym) -> (list sym))
-> (val empty-int (@ '() int))
() : (list int)
Bonus instantiation:
-> map
<proc> :
(forall ('a 'b)
(function ((function ('a) 'b)
(list 'a))
(list 'b)))
-> (@ map int bool)
<proc> : (function ((function (int) bool)
(list int))
(list bool))
Create your own!
Abstract over unknown type using type-lambda
-> (val id (type-lambda ('a)
(lambda (('a x)) x)))
id : (forall ('a) ('a -> 'a))
'a is type parameter (an unknown type)
This feature is parametric polymorphism
Two forms of abstraction:
|
term
|
type
|
lambda
|
function (arrow)
|
type-lambda
|
forall
|
Power comes at notational cost
Function composition
-> val o (type-lambda ('a 'b 'c)
(lambda ((('b -> 'c) f)
(('a -> 'b) g))
(lambda (('a x)) (f (g x))))))
o : (forall ('a 'b 'c)
(('b -> 'c) ('a -> 'b) -> ('a -> 'c)))
Aka o :
Instantiate by substitution:

Generalize with type-lambda:

*** A phase distinction embodied in code ***
-> (val x 3)
3 : int
-> (val y (+ x x))
6 : int
fun checkThenEval (d, (delta, gamma, rho)) =
let val (gamma', tystring) = elabdef (d, gamma, delta)
val (rho', valstring) = evaldef (d, rho)
val _ = print (valstring ^ " : " ^ tystring)
in (delta, gamma', rho')
end
Three environments --- what happens?:
Three environments revealed:

Exercise: Three environments:
Type Inference Intuition
Formalization
Constraints!
New topic: Type inference:

*** What type inference accomplishes ***
-> (define double (x) (+ x x))
double ;; uScheme
-> (define int double ((int x)) (+ x x))
double : (int -> int) ;; Typed uSch.
-> (define double (x) (+ x x))
double : int -> int ;; nML
*** What else type inference accomplishes ***
-> ((@ cons bool) #t ((@ cons bool) #f (@ '() bool)))
(#t #f) : (list bool) ;; typed uScheme
-> ( cons #t ( cons #f '() ))
(#t #f) : bool list ;; nML
Key ideas:
For each unknown type, introduce a fresh type variable
Enforce equality constraints
Introduce type-lambda at let/val bindings
{Examples}:

Let's do an example on the board
(val-rec double (lambda (x) (+ x x)))
What do we know?
Key idea: Record the constraint in a typing judgement.
a2 = int /\ a2 = int, { double : a1, x : a2 } |- (+ x x) : int
Example: if
(if y 1 0)
y has type ʹa3, 1 has type int, 0 has type int
Requires what constraints? (int = int, ʹa3 = 1bool`)
Example:
(if z z (- 0 z))
z has type ʹa3, 0 has type int, - has type int * int -> int
Requires what constraints? (ʹa3 = bool /\ int = int /\ ʹa3 = int)
Is this possible?
Why not?
let val app2 = (lambda (f x y)
(begin
(f x)
(f y)))
*** Exercise: Give the type of cc ***
let val cc = (lambda (nss) (car (car nss)))
*** Exercise: Give the type of cc ***
let val cc = (lambda (nss) (car (car nss)))
forall 'a . 'a list list -> 'a
*** Solve these constraints! ***
datatype con = ~ of ty * ty
| /\ of con * con
| TRIVIAL
infix 4 ~
infix 3 /\
{Solving Constraints}:
When is a constraint satisfied?:

{Examples}:

Board: which of these have solutions?
int ~ bool
int list ~ bool list
'a ~ int
'a ~ int list
'a ~ int -> int
'a ~ 'a
'a * int ~ bool * 'b
'a * int ~ bool -> 'b
'a ~ ('a, int)
'a ~ tau (arbitrary tau)
Question: in solving tau1 ~ tau2, how many potential cases are there to consider?
Question: how are you going to handle each case?
{Solving Constraint Conjunctions}:

So far
After this lecture, you can write solve, a function which, given a constraint C, has one of three outcomes:
Returns the identity substitution in the case where C is trivially satisfied
Returns a non-trivial substitution if C is satisfiable otherwise.
Calls unsatisfiableEquality in when C cannot be satisfied
You can also write a type inferencer ty for everything except let forms. (Coming Wednesday)
Type Inference Homework due Wednesday, April 6.
Next Week: Kathleen at Royal Society meeting in London
Kathleen's office hours cancelled.
Norman Ramsey lecturing on Smalltalk.
He'll ask: What have you covered in the first 10 weeks of class?
Type inference, continued
Moving from type schema to types (Instantiation)
Moving from types to type schema (Generalization)
Type Inference:

Key Idea:

Judgement forms:

Formalizing Type Inference:

Moving between type schema and types:
From Type Schema to Types:

Consider
Gamma = {fst : forall 'a 'b. 'a * 'b -> 'a, y : 'ay}
??, Gamma |- if (y, fst 2 3, 4) : ??
Imagine we ignore the freshness constraint when instantiating fst:
fst : 'ay * 'b -> 'ay
From if, we get the constraints:
'ay ~ bool
'ay ~ int
which aren't satisfiable. Which means this code would be erroneously flagged as an error.
Correct typing:
'ay ~ bool, Gamma |- if (y, fst 2 3, 4) : int
fst : 'a * 'a -> 'a
Gamma |- fst 2 #t
Application rule yields constraints:
'a ~ int
'a ~ bool
which aren't satisfiable. Which means this code would also be erroneously flagged as an error.
Correct typing:
Gamma |- fst 2 #t : int
From Types to Type Schema:

Generalize Function:

First Candidate VAL rule:
Example:

Second Candidate VAL rule:
VAL rule:
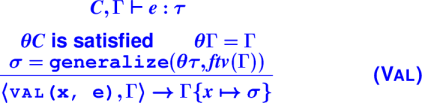
*** Let Examples ***
(lambda (ys)
(let ((s (lambda (x) (cons x '()))))
(pair (s 1) (s #t))))
(lambda (ys)
(let ((extend (lambda (x) (cons x ys))))
(pair (extend 1) (extend #t))))
(lambda (ys)
(let ((extend (lambda (x) (cons x ys))))
(extend 1)))
Let:

Idempotence:
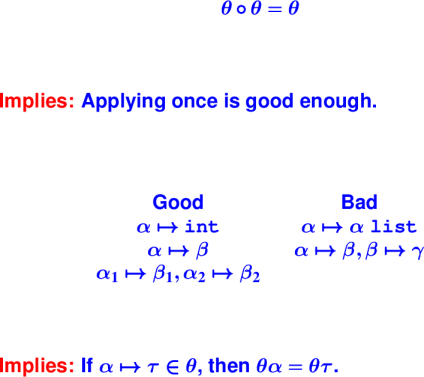
VAL-REC rule:
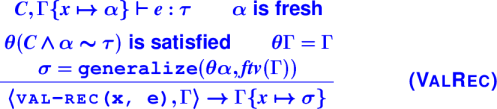
LetRec:
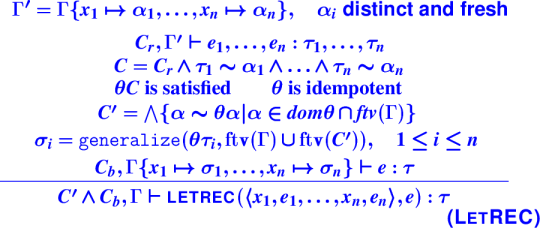
Forall things
Managing Quantified types
| FORALL contains all variables (because none are free in the context) |
FORALL contains variables not free in the context |
FORALL is empty |
| Generalize over all variables (because none are free in the context) |
Generalize over variables not free in the context |
Never generalize |
- Hardcopy solutions to tuScheme type checker available in class.
Instantiation of type schemas
Generalization: From types to type schemas
Splitting constraints for let rules
Where have we been?
- Programming in the small
- Expressive power
Success stories:
- First-class functions
- Algebraic data types and pattern matching
- Polymorphic type systems
What about big programs?
An area of agreement and a great divide:
INFORMATION HIDING
/ \
/ \
reuse / \ modular reasoning
/ \
/ \
OBJECTS MODULES
Two kinds of reuse:
- Inheritance: reuse implementations
- Subtyping: reuse interfaces
Don't conflate them!
We know that mixing code and data can create powerful abstractions (function closures)
Objects are another way to mix code and data
Pioneers were Nygaard and Dahl, who added objects to Algol 60, producing SIMULA-67, the first object-oriented language
Bjarne Stroustrup liked Simula but wanted complete control of costs, so he created C++
James Gosling wanted something a little cleaner and a little more like Simula, created Java
Microsoft funded C#
Objects are everywhere
Agglutination containing
A lot like a closure
A class is a way to define objects. It provides a recipe for object construction, defining the methods (code) and specifying how to initialize the instance variables (state) via constructors.
Not really useful for building small things
If you build a big, full-featured abstraction, you can easily use inheritance to build another, similar abstraction. Very good at adding new kinds of things that behave similarly to existing things.
Programs that are evolving
A particular kind of evolution: operations stay the same, but we add new kinds of things
For your homework, you'll take a Smalltalk system that has three kinds of numbers, and you'll add a fourth kind of number.
If you do anything at all interesting, your control flow becomes smeared out over half a dozen classes, and your algorithms are nearly impossible to understand.
Why Smalltalk?
- Another Turing Award
- Small, simple, pure objects
- Almost the complete language can be done in a relatively small interpreter
Alive and well today
- At the core of Ruby
- As an extension to C ("Objective C") for Apple products
Values are objects (even true, 3, "hello")
Even classes are objects!
There are no functions---only methods on objects
Slogan: Everything is an object.
Syntax:
mutable variables
message send
sequential composition of mutations and message sends (side effects)
"blocks" (really closures, objects and closures in one, used as continuations)
No if or while. These are implemented by passing continuations to Boolean objects.
(Smalltalk programmers have been indoctrinated and don't even notice)
Impcore syntax:

Smalltalk syntax:

Smalltalk syntax:

Environments
Dynamic semantics
- Main rule is method dispatch (complicated)
- The rest is familiar
The initial basis is enormous
- Why? To demonstrate the benefits of reuse, you need something big enough to reuse.
Types
There is no compile-time type system.
At run time, Smalltalk uses behavioral subtyping, known to Rubyists as "duck typing"
Look at SEND
- Message identified by name (messages are not values)
- Always sent to a receiver
- Optional arguments must match arity of message name
(no other static checking)
N.B. BLOCK and LITERAL are special objects.
*** Example: A bank account ***
-> (use finance.smt)
<class FinancialHistory>
<class DeductibleHistory>
-> (val account (initialBalance: FinancialHistory 1000))
<FinancialHistory>
-> (deposit:from: account 400 #salary)
1400
-> (withdraw:for: account 50 #plumber)
1350
-> (cashOnHand account)
1350
Protocol is Smalltalk term of art:
- The set of messages an object can respond to
- What it is supposed to do on receipt
Ruby dialect "duck typing" is a statement about protocols
Protocol is determined by the class of which an object is an instance
- About classes and instances, more later

Arities:
- Symbolic messages: arity 1
- Keyword messages: arity is number of colons
Every object gets not just the protocol but the implementations from its class. And a class can inherit from its superclass (more undefined terms) all the way up to class Object.
*** Simple examples ***
-> true
<True>
-> True
<class True>
-> Object
<class Object>
-> (isNil 3)
<False>
-> (isNil nil)
<True>
-> (println nil)
nil
nil
- Object = state + operations
- Class = way to define objects
- Six questions for Smalltalk
- Message passing
- Protocols
- Method Dispatch
- Blocks
- Collections
- Subtyping
- Double Dispatch
Blocks are closures
Blocks are objects
Booleans use continuation-passing style
Protocol for Booleans:

Booleans implemented with two classes True and False
Classes True and False:

Protocol for Booleans:

Board - Method dispatch
To answer a message:
Consider the class of the receiver
Is the method with that name defined?
If so, use it
If not, repeat with the superclass
Run out of superclasses?
"Message not understood"
{ message dispatched to class }:

*** Blocks manage loops ***
-> (val x 10)
-> (val y 20)
-> (whileTrue: [(<= x (* 10 y))]
[(set x (* x 3))])
nil
-> x
270
Protocol for blocks:

Key strategy for reuse in object-oriented languages: subtype polymorphism
A value of the subtype can be used wherever a value of the supertype is expected.
Board:
- SUBTYPE != SUBCLASS
- SUPERTYPE != SUPERCLASS
Only crippled languages like C++ identify subtype with subclass
Only the uneducated don't know the difference
Subtyping mathematically:
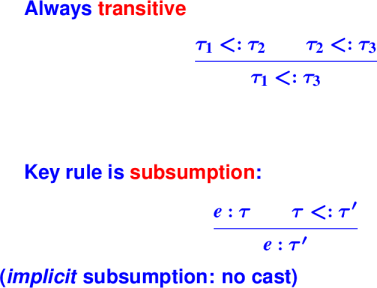
Subtyping is not inheritance:

Typical object-orientation:
- Code you execute depends on class of the receiver
What if you need to choose code based on both receiver and argument?
Solution: method name encodes both operation and type of argument
Examples:
addIntegerTo:
addFloatTo:
In class Float:
(method + (anInteger) (addFloatTo: anInteger self))
In class Integer:
(method addFloatTo: (aFloat) (<<code to add an Integer and a Float>>)
Consider evaluation of:
(+ 5.5 3)
Sends + message to object 5.5 with argument 3
Sends addFloatTo: message to 3 with argument 5.5
Code to add an Integer and a Float is executed.
Wide interfaces, reused
Algorithms smeared out over multiple classes
Behavioral subtyping, aka "Duck typing"
Old wine in new bottles
Initialization
Double dispatch
Information Hiding and Module Systems
Smalltalk collection classes
SML's Module System
Goal of objects is reuse
Key to successful reuse is a well-designed class hierarchy
Killer app: toolkits for building user interfaces
Smalltalk blue book is 90 pages on language, 300 pages on library
Lots of abstract classes
- Define protocols
- Build reusable stuff, just like class
Boolean
``Collection hierarchy'':

``Collections hierarchy'':

Collection mutators:

Collection observers:

Collection iterators:

Implementing collections:

Reusable methods:

Question: what's the most efficient way to find the size of a list?
Question: what's the most efficient way to find the size of an array?
Question: The addAll: method shows that the Collection class relies on subclass implementation of do: What happens if a subclass implements do: incorrectly?
{species method}:

{The four crucial Collection methods}:

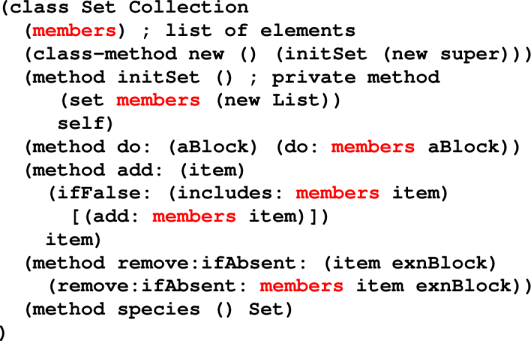
Most subclass methods work by delegating all or part of work to list members
N.B. Set is a client of List, not a subclass!
Next example highlight: class method and super!

{Information Hiding in Smalltalk}:

- Kathleen's Tuesday office hours moved to Thursday 2-3
Signatures
Structures
Functors
Unlocking the final door for building large software systems
You have all gotten good at first-class functions, algebraic data types, and polymorphic types
Modules are the last tool you need to build big systems
Functions of a true module system:
Hide representations, implementations, private names
"Firewall" separately compiled units (promote independent compilation)
Possibly reuse units
Real modules include separately compilable interfaces and implementations
Designers almost always choose static type checking, which should be "modular" (i.e., independent)
C and C++ are cheap imitations
- C doesn't provide namespaces
- C++ doesn't provide modular type checking for templates
Collect declarations
- Unlike definition, provides partial information about a name (usually environment and type)
Things typically declared:
Terminology: a module is a client of the interfaces it depends on
Roles of interfaces in programming:
The best-proven technology for structuring large systems.
Means of hiding information (ask "what secret does it hide?")
A way to limit what we have to understand about a program
- Estimated force multiplier x10
A contract between programmers
- Essential for large systems
- Parties might be you and your future self
Interface is the specification or contract that a module implements
- Includes contracts for all declared functions
Two approaches to writing interfaces
Interface "projected" from implementation:
- No separate interface
- Compiler extracts from implementation
(CLU, Java class, Haskell, Oberon)
- When code changes, must extract again
- Few cognitive benefits
Full interfaces:
- Distinct file, separately compiled
(Caml, Java interface, Modula, Ada)
- Implementations can change independently
- Full cognitive benefits
Holds all dynamically executed code (expressions/statements)
May include private names
May depend only on interfaces, or on interfaces and implementations both (max cognitive benefits when all dependency is mediated by interfaces)
Dependencies may be implicit or explicit (import, require, use)
The Perl of module languages?
Has all known features
Supports all known styles
Rejoice at the expressive power
Weep at the terminology, the redundancy, the bad design decisions
What we've been using so far is the core language
Modules are a separate language layered on top.
ML module terminology
Interface is a signature
Implementation is a structure
Generic module is a functor
Structures and functors match signature
Analogy: Signatures are the ``types'' of structures.
Signature says what's in a structure
Specify types (w/kind), values (w/type), exceptions.
Ordinary type examples:
type t // abstract type, kind *
eqtype t
type t = ... // 'manifest' type
datatype t = ...
Type constructors work too
type 'a t // abstract, kind * => *
eqtype 'a t
type 'a t = ...
datatype 'a t = ...
*** Signature example: Integers ***
signature INTEGER = sig
eqtype int (* <-- ABSTRACT type *)
val ~ : int -> int
val + : int * int -> int
val - : int * int -> int
val * : int * int -> int
val div : int * int -> int
val mod : int * int -> int
val > : int * int -> bool
val >= : int * int -> bool
val < : int * int -> bool
val <= : int * int -> bool
val compare : int * int -> order
val toString : int -> string
val fromString : string -> int option
end
Implementations of integers
A selection...
structure Int :> INTEGER
structure Int31 :> INTEGER (* optional *)
structure Int32 :> INTEGER (* optional *)
structure Int64 :> INTEGER (* optional *)
structure IntInf :> INTEGER (* optional *)
*** Queues in Standard ML: A Signature ***
signature QUEUE = sig
type 'a queue (* another abstract type *)
exception Empty
val empty : 'a queue
val put : 'a * 'a queue -> 'a queue
val get : 'a queue -> 'a * 'a queue (* raises Empty *)
(* LAWS: get(put(a, empty)) == (a, empty)
...
*)
end
*** Queues in Standard ML: A Structure ***
structure Queue :> QUEUE = struct
type 'a queue = 'a list
exception Empty
val empty = []
fun put (x,q) = q @ [x]
fun get [] = raise Empty
| get (x :: xs) = (x, xs)
(* LAWS: get(put(a, empty)) == (a, empty)
...
*)
end
Exercise: Signature for a Stack
structure Stack = struct
type 'a stack = 'a list
exception Empty
val empty = []
val push = op ::
fun pop [] = raise Empty
| pop (tos::rest) = tos
end
Exercise: Signature for a Stack
signature STACK = sig
type 'a stack
exception Empty
val empty : 'a stack
val push : 'a * 'a stack -> 'a stack
val pop : 'a stack -> 'a
end
*** Dot notation to access elements ***
structure Queue :> QUEUE = struct
type 'a queue = 'a list
exception Empty
val empty = []
fun put (q, x) = q @ [x]
fun get [] = raise Empty
| get (x :: xs) = (x, xs)
end
fun single (x:'a) : 'a Queue.queue =
Queue.put(Queue.empty, x)
Signature Matching
Well-formed
structure Queue :> QUEUE = QueueI
if the principal signature of QueueI matches the ascribed signature QUEUE. Intuitively:
Every type in QUEUE must have a matching type in QueueI
Every exception in QUEUE must have a matching exception in QueueI
Every value in QUEUE must have a matching value in QueueI with at least as general a type.
Signature Ascription
Signature Ascription is the process of attaching a signature to a structure.
Transparent Ascription: type equalities are revealed.
structure strid : sig_exp = struct_exp
Opaque Ascription: type equalities are hidden.
structure strid :> sig_exp = struct_exp
Transparent Ascription
Example:
structure IntLT : ORDERED = struct
type t = int
val le = (op <)
val eq = (op =)
end
Valid: IntLT.t = int
Opaque Ascription
Example:
structure Queue :> QUEUE = struct
type 'a queue = 'a list
exception Empty
val empty = []
fun put (x, q) = q @ [x]
fun get [] = raise Empty
| get (x :: xs) = (x, xs)
end
Not valid: 'a Queue.queue = 'a list
Functors
A Functor is a function on modules.
functor AddSingle(Q:QUEUE) =
struct
structure Queue = Q
fun single x = Q.put (Q.empty, x)
end
Instantiating Functors
Functor applications are evaluated at compile-time.
functor AddSingle(Q:QUEUE) =
struct
structure Queue = Q
fun single x = Q.put (Q.empty, x)
end
structure QueueS = AddSingle(Queue)
structure EQueueS = AddSingle(EQueue)
where EQueue is a more efficient implementation
Sharing Constraints:

Why functors?:

Hardcopy solutions to uSmalltalk assignment available in class.
SML assignment due Wednesday, April 27
- Extended SML Example: Computations
Error-tracking Interpreter
An Extended Example
Lots of interfaces using ML signatures
Idea of how to compose large systems
Use case for the error summaries from recitation
Some ambitious, very abstract abstractions---it's almost the last week of class, and you should see something ambitious.
Practice implementing functors
Error modules: Three common implementations (all covered in recitation)
Your obligations: two types, three functions, algebraic laws
*** Classic ``accumulator'' for errors ***
signature ERROR = sig
type error (* a single error *)
type summary (* summary of what errors occurred *)
val nothing : summary (* no errors *)
val <+> : summary * summary -> summary (* combine *)
val oneError : error -> summary
(* laws: nothing <+> s == s
s <+> nothing == s
s1 <+> (s2 <+> s3) == (s1 <+> s2) <+> s3
// associativity
*)
end
*** First Error Implementation ***
structure FirstError :>
ERROR where type error = string
and type summary = string option =
struct
type error = string
type summary = string option
val nothing = NONE
fun <+> (NONE, s) = s
| <+> (SOME e, _) = SOME e
val oneError = SOME
end
*** All Error Implementation ***
structure AllErrors :>
ERROR where type error = string
and type summary = string list =
struct
type error = string
type summary = error list
val nothing = []
val <+> = op @
fun oneError e = [e]
end
Ambitious! (will make your head hurt a bit)
Computations either:
return a value
produce an error
Errors must be threaded through everything :-(
*** Exercise: Simple arithmetic interpreter ***
(* Given: *)
datatype 'a comp = OK of 'a | Err of AllErrors.summary
datatype exp = LIT of int
| PLUS of exp * exp
| DIV of exp * exp
(* Write an evaluation function that tracks errors. *)
val eval : exp -> int comp = ...
*** Exercise: LIT and PLUS cases ***
fun eval (LIT n) = OK n
| eval (PLUS (e1, e2)) =
(case (eval e1)
of OK v1 => (case (eval e2)
of OK v2 => OK (v1 + v2)
| err2 as (Err s2) => err2)
| err1 as (Err s1) => (case (eval e2)
of OK v2 => err1
| err2 as (Err s2) =>
Err (AllErrors.<+> (s1, s2))))
*** Exercise: DIV case ***
| eval (DIV (e1, e2)) =
(case (eval e1)
of OK v1 => (case (eval e2)
of OK v2 =>
(case v2
of 0 => Err (AllErrors.oneError "Div by 0.")
| _ => OK (v1 div v2))
| err2 as (Err s2) => err2)
| err1 as (Err s1) => (case (eval e2)
of OK v2 => err1
| err2 as (Err s2) =>
Err(AllErrors.<+> (s1, s2))))
That's really painful!
We can extend the computation abstraction with sequencing operations to help.
*** Combining generic computations ***
signature COMPUTATION = sig
type 'a comp (* Computation! When run, results in
value of type 'a or error summary. *)
(* A computation without errors always succeeds. *)
val succeeds : 'a -> 'a comp
(* Apply a pure function to a computation. *)
val <$> : ('a -> 'b) * 'a comp -> 'b comp
(* Application inside computations. *)
val <*> : ('a -> 'b) comp * 'a comp -> 'b comp
(* Computation followed by continuation. *)
val >>= : 'a comp * ('a -> 'b comp) -> 'b comp
end
eval e1 + eval e2
(op +) (eval e1, eval e2)
curry (op +) (eval e1) (eval e2)
curry (op +) <$> eval e1 <*> eval e2
The first three versions are not well typed. Why?
The last version will thread errors through the compuation behind the scenes.
Note:
eval e1, eval e2 : int comp
curry (op +) : int -> (int -> int)
<$> : (int -> (int -> int)) * (int comp) -> (int -> int) comp
<*> : (int -> int) comp * int comp -> int comp
curry (op +) <$> eval e1 : (int -> int) comp
let pa = curry (op +) <$> eval e1
note by above, pa : (int -> int) comp
pa <*> eval e2 : int comp
*** {Buckets of \emph{generic} algebraic laws} ***
succeeds a >>= k == k a // identity
comp >>= succeeds == comp // identity
comp >>= (fn x => k x >>= h) == (comp >>= k) >>= h
// associativity
succeeds f <*> succeeds x == succeeds (f x) // success
...
*** Environments using ``computation'' ***
signature COMPENV = sig
type 'a env (* environment mapping strings
to values of type 'a *)
type 'a comp (* computation of 'a or
an error summary *)
val lookup : string * 'a env -> 'a comp
end
*** Payoff! ***
functor InterpFn(structure Error : ERROR
structure Comp : COMPUTATION
structure Env : COMPENV
val zerodivide : Error.error
val error : Error.error -> 'a Comp.comp
sharing type Comp.comp = Env.comp) =
struct
val (<*>, <$>, >>=) = (Comp.<*>, Comp.<$>, Comp.>>=)
(* Definition of Interpreter *)
end
*** Definition of intepreter, continued ***
datatype exp = LIT of int
| VAR of string
| PLUS of exp * exp
| DIV of exp * exp
fun eval (e, rho) =
let fun ev(LIT n) = Comp.succeeds n
| ev(VAR x) = Env.lookup (x, rho)
| ev(PLUS (e1, e2)) = curry op + <$> ev e1 <*> ev e2
| ev(DIV (e1, e2)) = ev e1 >>= (fn n1 =>
ev e2 >>= (fn n2 =>
case n2
of 0 => error zerodivide
| _ => Comp.succeeds
(n1 div n2)))
in ev e
end
*** {Extend a signature with \lit{include}} ***
signature ERRORCOMP = sig
include COMPUTATION
structure Error : ERROR
datatype 'a result = OK of 'a
| Err of Error.summary
val run : 'a comp -> 'a result
val error : Error.error -> 'a comp
end
*** {Let's build \lit{ERRORCOMP}} ***
functor ErrorCompFn(structure Error : ERROR) :>
ERRORCOMP where type Error.error = Error.error
and type Error.summary = Error.summary =
struct
structure Error = Error
datatype 'a result = OK of 'a
| Err of Error.summary
type 'a comp = 'a result
fun run comp = comp
fun error e = Err (Error.oneError e)
fun succeeds = OK
...
end
*** ``Computations Abstraction" = a monad ***
Haskell has syntactic support to make
monadic programming easier:
eval :: Exp -> Hopefully Int
eval (LIT i) = return i
eval (PLUS e1 e2) = do {
v1 <- eval e1;
v2 <- eval e2;
return (v1 + v2) }
eval (DIV e1 e2) = do {
v1 <- eval3 e1;
v2 <- eval3 e2;
if v2 == 0 then Error "divby0" else return (v1 `div` v2)}
Theoretical underpinnings for most programming langauges (all in this class).
Church-Turing Thesis: Any computable operator can be expressed as an encoding in lambda calculus
Test bench for new language features
Only three syntactic forms:
M ::= x | \x.M | M M'
Everything is programming with functions
First example:
(\x.\y.x) M N --> (\y.M) N --> M
Crucial: argument N is never evaluated (could have an infinite loop)
Everything is continuation-passing style
Q: Who remembers the boolean equation solver?
Q: What classes of results could it produce?
A: success, failure
Q: How were the results delivered?
A: calling continuations
Q: How shall we do Booleans?
A: true continuation, false continuation
Booleans take two continuations:
true = \t.\f.t
false = \t.\f.f
if M then N else P = ??? (* M N P *)
if = \b.\t.\e.b t e
How many ways can pairs be created? (A: one, pair constructor)
How many continuations? (A: one, corresponding to the pair)
What information does it expect? (A: the two elements of the pair)
What are the algebraic laws?
fst (pair x y) = x
snd (pair x y) = y
Code pair, fst, and snd
pair x y f = f x y
fst p = p (\x.\y.x)
snd p = p (\x.\y.y)
pair = \x.\y.\f.f x y
fst = \p.p (\x.\y.x)
snd = \p.p (\x.\y.y)
How many ways can lists be created? (A: two, nil and cons)
How many continuations? (A: two, one for each)
What does each continuation expect? (A: nil - nothing; cons - hd, tl)
For each creator, what are the laws regarding its continuations?
cons y ys n c = c y ys
nil n c = n
car xs = xs error (\y.\ys.y)
cdr xs = xs error (\y.\ys.ys)
null? xs = xs true (\y.\ys.false)
cons = \y.\ys.\n.\c.c y ys
nil = \n.\c.n
car = \xs.xs error (\y.\ys.y)
cdr = \xs.xs error (\y.\ys.ys)
null? = \xs.xs true (\y.\ys.false)
Wikipedia good: "Church numerals"
Key Idea: The value of a numeral is the number of times it applies its argument function.
Encoding natural numbers:

Church Numerals:
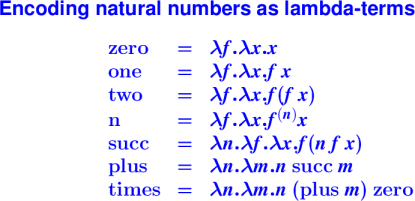
*** Church Numerals in $\lambda$ ***
zero = \f.\x.x;
succ = \n.\f.\x.f (n f x);
plus = \n.\m.n succ m;
times = \n.\m.n (plus m) zero;
...
-> four;
\f.\x.f (f (f (f x)))
-> three;
\f.\x.f (f (f x))
-> times four three;
\f.\x.f (f (f (f (f (f (f (f (f (f (f (f x)))))))))))
Taking stock:
bools
pairs
lists
numbers
Question: What's missing from this picture?
Answer: We're missing recursive functions.
Astonishing fact: we don't need letrec or val-rec (Wednesday)
New kind of semantics: small-step
New judgment form
M --> N ("M reduces to N in one step")
No context!! No turnstile!!
Just pushing terms around == calculus
{Reduction rules}:

The substitution in the beta rule is the heart of the lambda calculus
- It's hard to get right
- It's a stupid design for real programming (shell, tex, tcl)
- It's even hard for theorists!
- But it's the simplest known thing
Board examples:
Are these functions the same?
\x.\y.x
\w.\z.w
Are these functions the same?
\x.\y.z
\w.\z.z
Free variables:
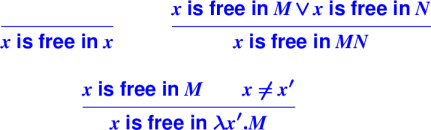
Examples of free variables:
\x. + x y (* y is free *)
\x.\y. x (* nothing is free *)
*** Exercise: Free Variables ***
What are the free variables in:
\x.\y. y z
\x.x (\y.x)
\x.\y.\x.x y
\x.\y.x (\z.y w)
y (\x.z)
(\x.\y.x y) y
*** Exercise: Free Variables ***
What are the free variables in:
\x.\y. y z - z
\x.x (\y.x) - nothing
\x.\y.\x.x y - nothing
\x.\y.x (\z.y w) - w
y (\x.z) - y z
(\x.\y.x y) y - y
Capture-avoiding substitution:
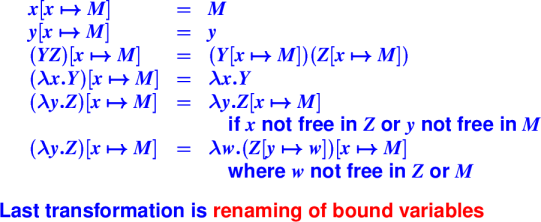
Example:
(\yes.\no.yes)(\time.no) ->
\z.\time.no
and never
\no.\time.no // WRONG!!!!!!
Must rename the bound variable:
(\yes.\no.yes) (\time.no) tuesday
->
(\yes.\z.yes) (\time.no) tuesday
->
(\z.\time.no) tuesday
->
\time.no
{Renaming of bound variables}:
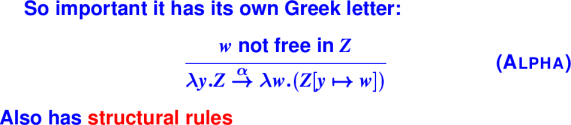
SML assignment due tonight at midnight.
Lambda calclulus assignment due Monday at midnight.
Monday: Review. Bring Questions!
Final: Friday, May 6, 8:30 - 10:30 in Braker 001 (class)
Review:
(\yes.\no.yes) (\time.no) tuesday
-> WRONG!!!
(\no.\time.no) tuesday
->
\time.tuesday
Must rename the bound variable:
(\yes.\no.yes) (\time.no) tuesday
-> (alpha)
(\yes.\z.yes) (\time.no) tuesday
-> (beta)
(\z.\time.no) tuesday
-> (beta)
\time.no
{Conversion/Reduction Rules}:

Capture-avoiding substitution:

Nondeterminism of conversion:
A
/ \
V V
B C
Now what??
Church-Rosser Theorem:
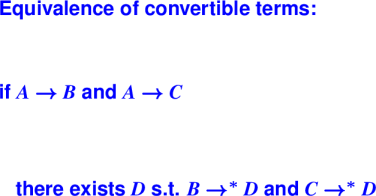
Given a beta-redex
(\x.M) N
do the beta-reduction only if N is in normal form
- Good model for ML and Scheme, so-called "call by value" languages
- Think "arguments before bodies"
Q: Does applicative order ever prevent you from making progress?
A: No. We can prove it by induction on the number of lambdas in N
Normal-order reduction:

Always choose leftmost, outermost redex
"Normal-order" stands for produces a normal form, not for "the normal way of doing things"
Normal-order illustration:

Normal-order is not your typical call-by-value semantics!
What solves this equation?:
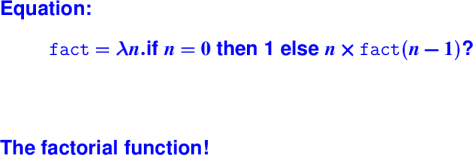
Exercise
Is there a solution? Is it unique? If so, what is it?
f1 = \n.\m.(eq? n m) n
(plus n (f1 (succ n) m));
f2 = \n.f2 (isZero? n 100 (pred n));
f3 = \xs.xs nil (\z.\zs.cons 0 (f3 zs));
f4 = \xs.\ys.f4 ys xs;
Exercise answers
f1 = \n.\m.(eq? n m) n
(plus n (f1 (succ n) m));
; sigma (sum from n to m)
f2 = \n.f2 (isZero? n 100 (pred n));
; no unique solution (any constant f2)
f3 = \xs.xs nil (\z.\zs.cons 0 (f3 zs));
; map (const 0)
f4 = \xs.\ys. f4 xs ys;
; not unique: constant functions ...
Recursion = Fixed point:
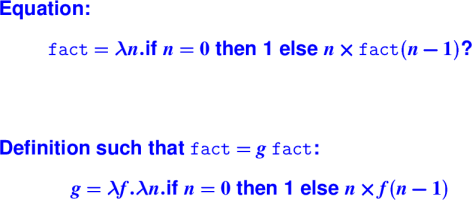
Why the term "Fixed point"?
The function g doesn't "move/change" x.
x = g x
Suppose g F = F. Proof that F is factorial.
For all n, g F n = n!, by induction:
Basis: n = 0.
F 0 = g F 0 = 1
Induction: n > 0. F n = { by assumption } g F n = { definition of g } if n = 0 then 1 else n * F (n-1) = { assumption, n > 0 } n * F (n-1) = { induction hypothesis } n * (n-1)! = { definitiion of factorial } n!
Your turn:
*** Conversion to fixed point ***
length = \xs.null? xs 0 (+ 1 (length (cdr xs)))
lg = \lf.\xs.null? xs 0 (+ 1 (lf (cdr xs)))
Note that: lg length = length
A recursive function f implies there is a higher-order function g such that f = g f.
Amazing fact: Given g, we can compute f, the fixed-point of g.
One startling idea
You can define a fixed-point operator fix
Algebraic Law: fix g = g (fix g)
Use fix g to define recursive functions!
{Y combinator can implement fix}:

Why is it called a "calculus"?
Differential calculus example: d/dx x^n equals what?
What's going on here?
Answer: pure formal manipulation
No understanding of functions required; you could write a program to do it (and many people have)
What's the role of calculi in computer science:
Lambda calculus:
Process calculus:
Pi calculus:
- Mobile computing and mobile agents
Ambient calculus:
- Security and protection domains
Why so many calculi? They have simple metatheory and proof technique.
Lambda calclulus assignment due tonight at midnight.
Final: Friday, May 6, 8:30 - 10:30 in Braker 001 (class)
May bring one double-sided page of notes
ML
Datatypes
Declarations introduce type constructor & data constructors
Datatypes can be recursive
Type variables allow polymorphic data structures
ML Pattern Matching
Deconstruct values: datatypes, lists, tuples, ...
Bind variables
Appear in function definitions, case expressions, and let bindings
ML Exceptions
- Declarating, raising, handling
Type Systems: Big Idea
Static vs. Dynamic Typing
Expressiveness (+ Dynamic)
Don't have to worry about types (+ Dynamic)
Dependent on input (- Dynamic)
Runtime overhead (- Dynamic)
Serve as documentation (+ Static)
Catch errors at compile time (+ Static)
Used in optimization (+ Static)
Type Systems: Big Idea
Type Systems: Mechanics
Monomorphic and Polymorphic Types
Types, Type Constructors, Quantified Types (∀α.τ)
Kinds (κ) classify types:
well-formed,
types (*),
type constructors: κ ⇒ κ
Type Environments: type identifiers → kinds
Typing Rules
- Introduction and Elimination forms
Type Checking
Induction and Recursion
Hindley-Milner Type Inference: Big Idea
Hindley-Milner Type Inference: Mechanics
Use fresh type variables to represent unknown types
Generate constraints that collect clues
Solve constraints when introducing quantifiers
Compromises to preserve decideability:
Object-Oriented Programming: Big Ideas
"Programming-in-the-medium"
Advantages and Disadvantages
Enables code reuse
Easy to add new kinds of objects
Hard to add new operations
Algorithms smeared across many classes
Hard to know what code is executing
Good match for GUI programming
Smalltalk mantra: Everything is an Object
- Can redefine basic operations
Object-Oriented Programming: Mechanics
Classes and objects
Computation via sending messages
Double-dispatch
Inheritance for implementation reuse
Subtyping ("duck typing") for client code reuse
Subtyping is not Inheritance
self and super
Blocks to code anonymous functions & continuations
Module Systems a la SML: Big Ideas
Module Systems a la SML: Mechanics
Signatures describe interfaces
Structures provide implementations
Signature ascription hides structure contents (Heap :> HEAP)
Functors
Lambda Calculus: Big Ideas
Lambda Calculus: Mechanics
Bound vs. Free variables
α-conversion: Names of bound variables don't matter.
β-reduction: Models computation.
Capture-avoiding substitution (Why important?)
Recursion via fixed points
Y combinator calculates fixed points:
- Y = λf.(λx.f(x x))(λx.f(x x))
Programming Experience
Recursion and higher-order functions are now second-nature to you.
- You'll miss pattern matching and algebraic data types in any language you use that doesn't have them!
C for impcore (imperative language)
Scheme (dynamically typed functional language)
ML (statically typed functional language)
uSmalltalk (dynamically typed OO language)
Built substantial pieces of code
SAT solver using continuations
Type checker (ML pattern matching!)
Type inference system (using constraints, reading typing rules)
BigNums (Power of OO abstractions; resulting challenges)
Game solver (SML module system)
Where might you go from here?
Haskell
Prolog
Ruby
Additional Courses
Compilers
Special Topics:
Domain-specific languages
Probabilisitic Programming Languages
Advanced Functional Programming
Big-picture questions?
Studying for the Exam
Exam will be like midterm
Expect to write some code (SML, uSmalltalk) 2ex
Review homework assignments
Review recitation materials
Make sure you understand Big Ideas/tradeoffs
Other Questions?
Course feedback
In future courses
Congratulations!
Back to class home page