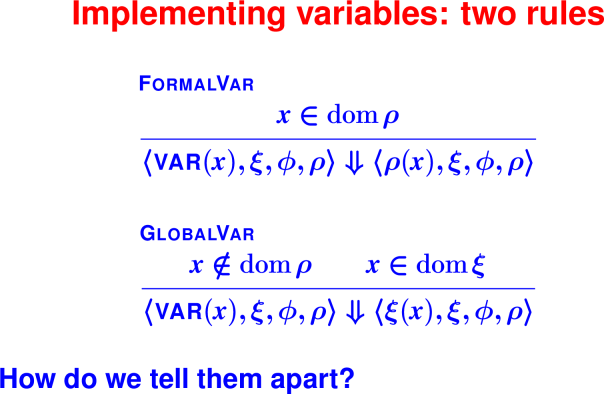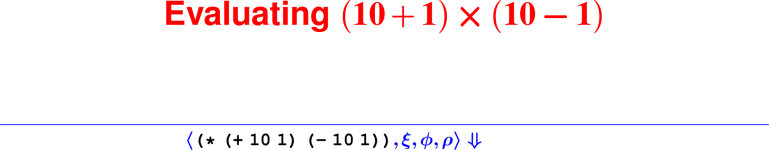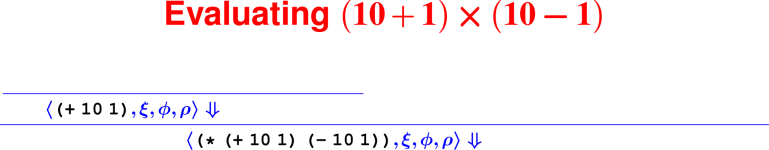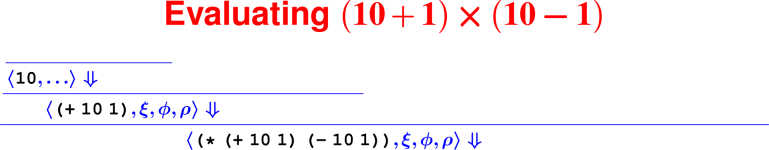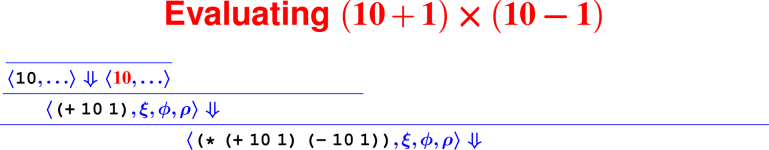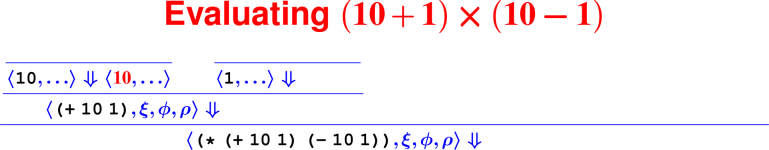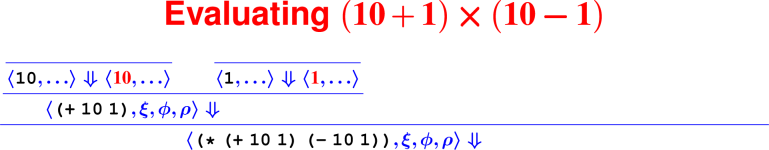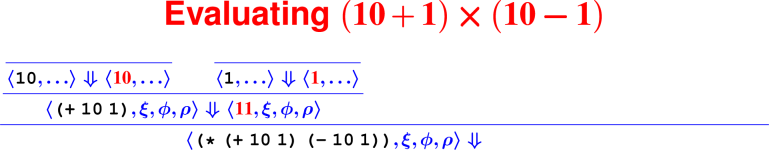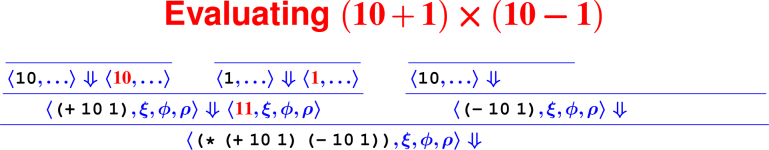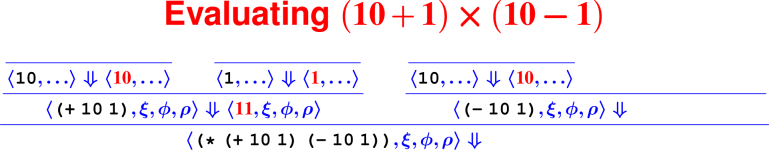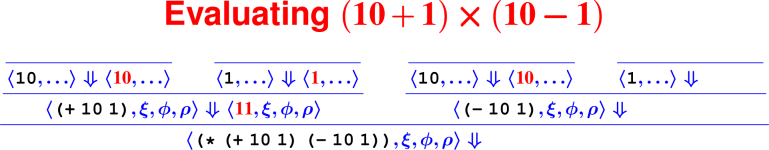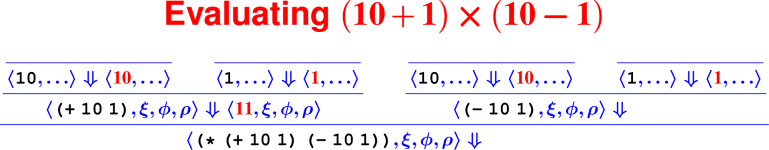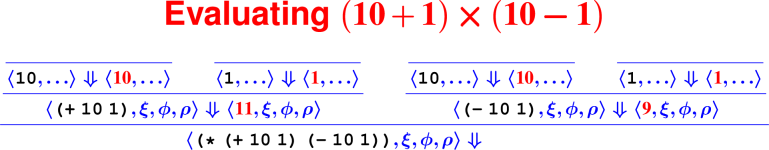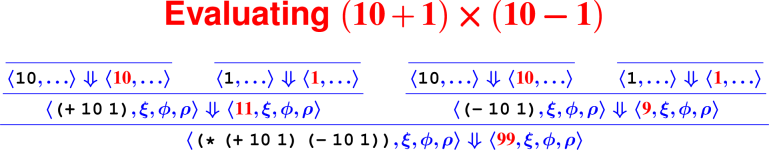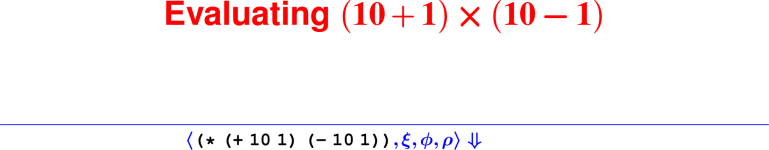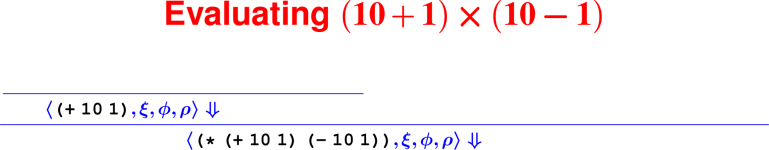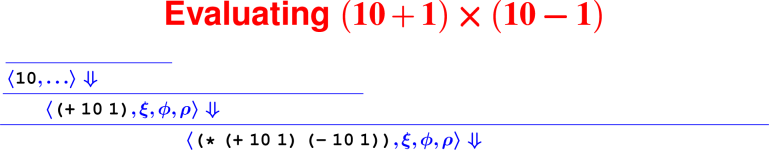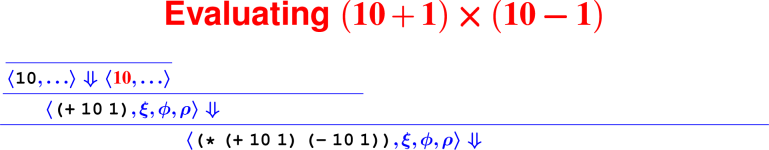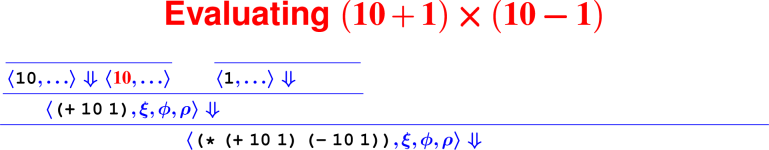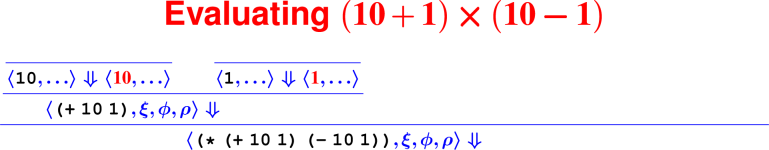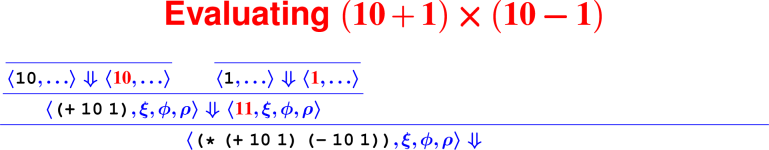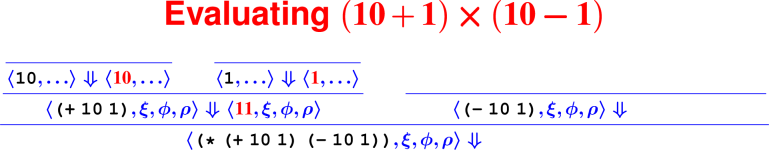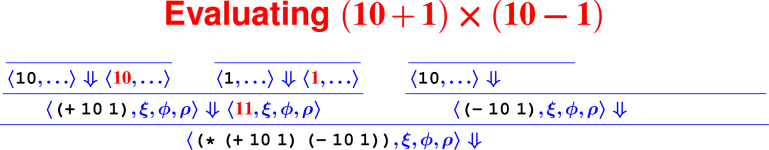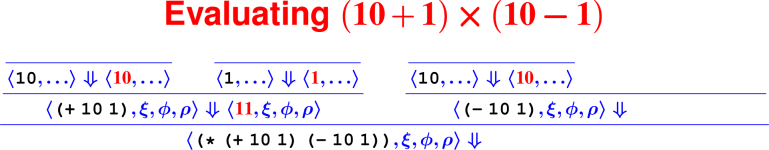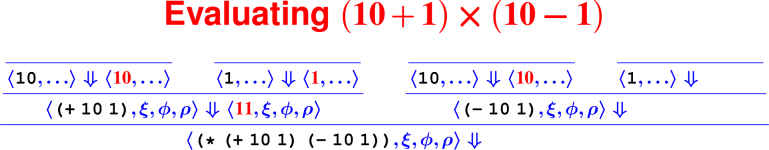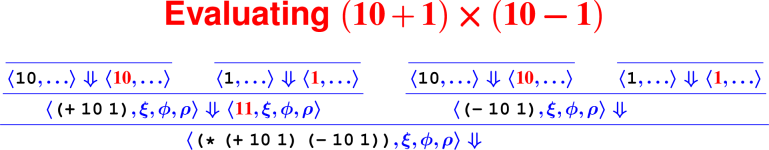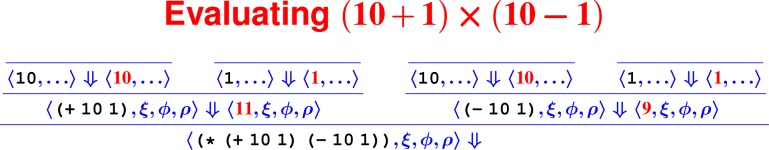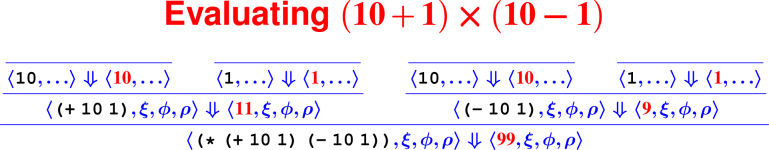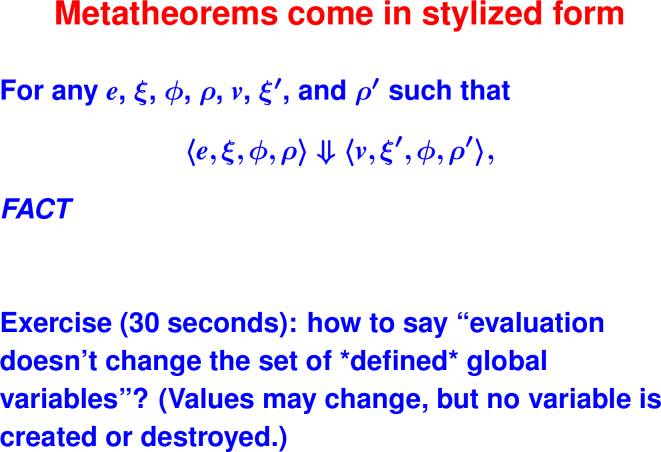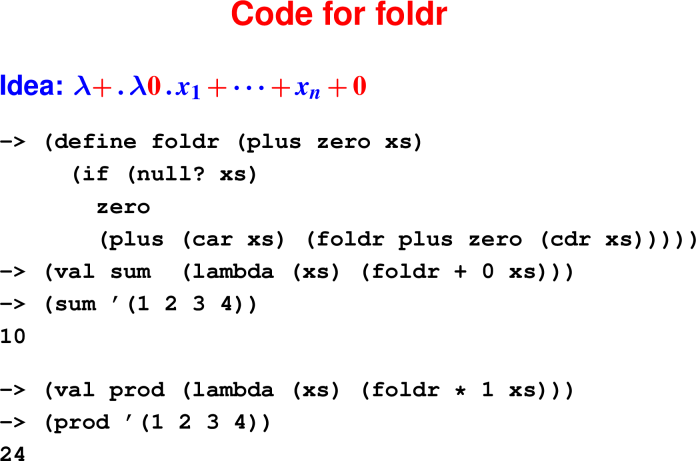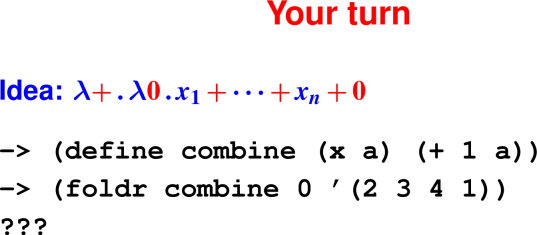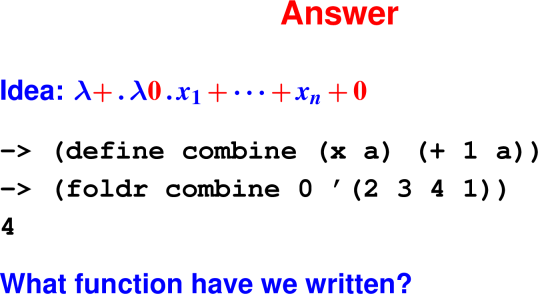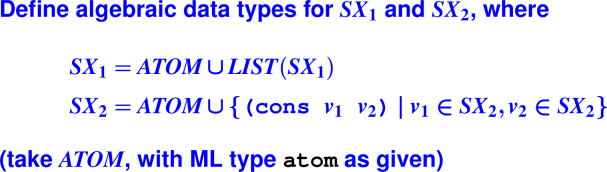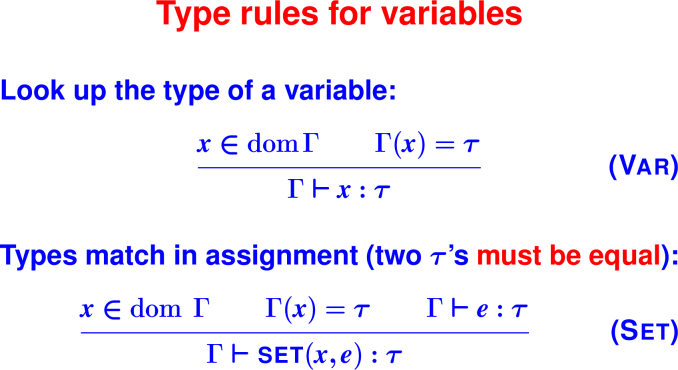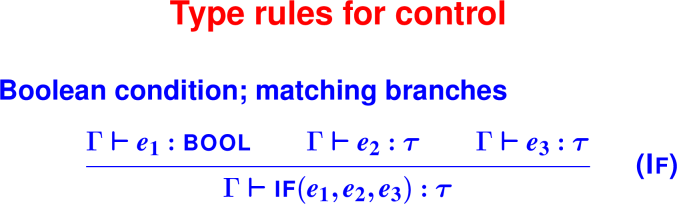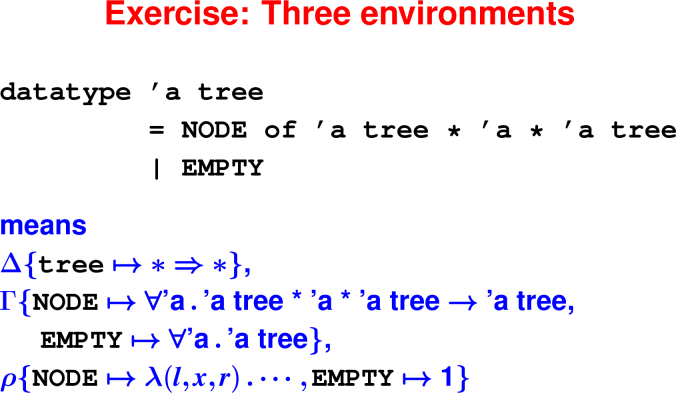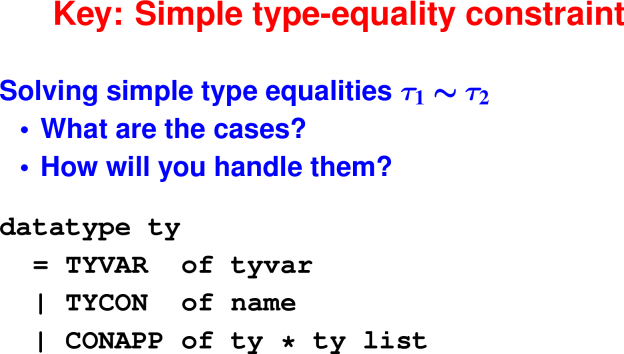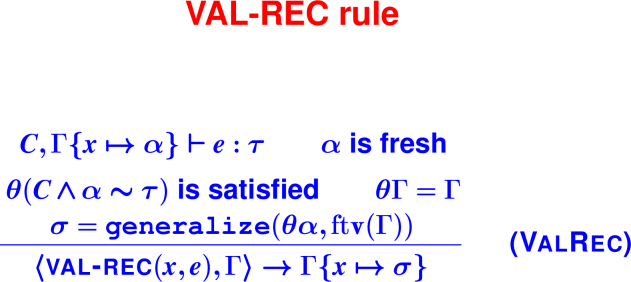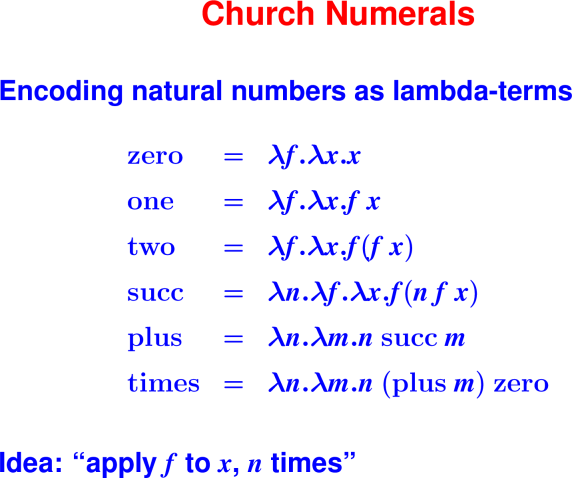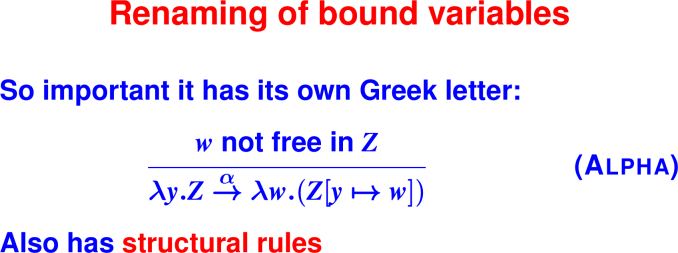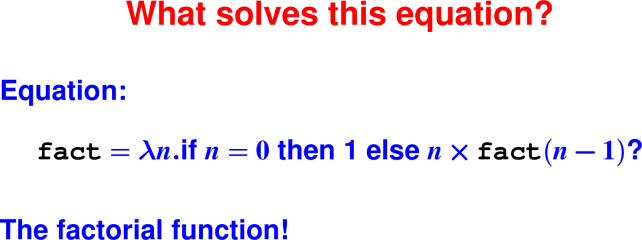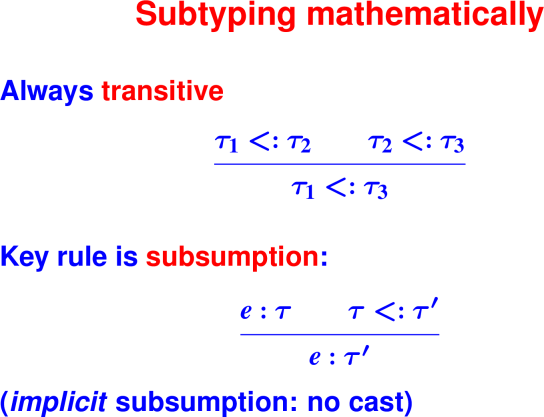Photos from Lecture
There is a shared album with photos of lecture. Anybody can add photos.
16 January 2019: Introduction to Comp 105
There are PDF slides for 1/17/2019.
Handout: Experiences of successful 105 students
Handout: Lessons in program design
Handout: Homework (photograph, due Jan 22)
Handout: Homework (Impcore, due Jan 29)
There will be a shared album with photos of lecture. Anybody can add photos.
Introduction
My pronouns are he, him, his.
Please call me “Norman,” “Professor Ramsey,” or “Mr Ramsey”
Why we are here
- Write code from scratch
- In a language you’ve never seen
- That sails past code review
What it involves:
- Programming practice (emphasize widely used features: functions, types, modules, objects)
- Mathematical description (how things work, see patterns)
(Example: see patterns of recursion in homework)
Today:
- Start with technical work
- Then a little about experience and expectations
What is a programming language?
What is a PL? Think. Then pair. Then share.
First three classes: new ways of thinking about stuff you already know
Syntactic structure: induction
Numerals
Show some example numerals
Numerals:
2018
73
1852Not numerals:
3l1t3
2+2
-12Q: What does a numeral stand for?
That is, if a numeral appears in the syntax, what sort of value flies around at run time?
Q: Does every numeral stand for one of these things?
Q: How many of them are there?
Q: How many numerals are there?
In-class Exercise: Inductive definitions of numerals
Write an inductive definition of numerals
There is more than one! When you finish one, look for another
Value structure: induction again
In-class exercise: inductive definition of natural number
- Again, there is more than one
- What makes it easy to know meaning of numerals?
Writing code with recursion and induction
Data-driven design process. Connections to design ideas from 1970s, 1980s, 1990s, plus test-driven development (2000s).
Syntax in programming languages
Concrete Syntax
Programming-languages people are wild about compositionality.
Build sensible things from sensible pieces using just a few construction principles.
Example: expressions, e1 + e2
Syntactic structure of Impcore
Watch for syntactic categories, syntactic composition
Live coding in Impcore
Try square function. E.g., (square (+ 2 2))
23 January 2019: Abstract syntax and operational semantics
There are PDF slides for 1/24/2019.
Handout: 105 Impcore Semantics, Part 1
Live coding: Impcore
All fours, tests, big literals
square, negated, interactive check-expect
Review: algebraic laws
Approaching 105
100-level course
Responsibility for your own learning: lecture is the tip of the iceberg
Announcement: Syllabus scavenger hunt (participation grades)
Systematic programming process: we can’t observe process, but it will affect your time spent by a factor of 2, 3, or 4.
Awareness of your own learning: Metacognition
Office hours
Students: go to office hours! An idle TA is an unhappy TA.
Review
Short discussion: One thing you learned in the first class
Language: syntax, rules/organization/grammar
Programming language: you can run it (values)
Preparing for a language you’ve never seen before
You need a vocabulary. It will involve math.
This week: abstract syntax and operational semantics (next homework)
Concrete and abstract Syntax
Programming-languages people are wild about compositionality.
- Build sensible things from sensible pieces using just a few construction principles.
Example of compositionality: concrete syntax (grammar)
- How many different kinds of things can be composed: syntactic categories
C/C++ Impcore
Compute w/ existing names
- value and behavior exp exp
- just behavior stm
Add new names to program
- initialized def def
- uninitialized declExample rules of composition:
C/C++: expressions, definitions, statements
Impcore
Programming-language semantics
“Semantics” means “meaning.”
We want a computational notion of meaning.
What problem are we trying to solve?
Know what’s supposed to happen when you run the code
Ways of knowing:
- People learn from examples
- You can build intuition from words
(Book is full of examples and words) - To know exactly, unambiguously, you need more precision
(For homework, you’ll prove that our specification is unambiguous.)
Why bother with precise semantics?
(Needed to build implementation, tests)
Same reason as other forms of math:
- Distill down your understanding and express it
- Prove properties people care about (e.g., private information doesn’t leak; device driver can’t bring kernel down)
- Most important for you: things that look different are actually the same
The programming languages you encounter after 105 will certainly look different from what we study this term. But most of them will actually be the same. Studying semantics helps you identify that.
The idea: your new skills will apply
Behavior decomposes
What happens when we run
(* y 3)?
We must know something about *, y, 3, and function application.
Knowledge is expressed inductively
Atomic forms: Describe behavior directly (e.g., constants, variables)
Compound forms: Behavior specified by composing behaviors of parts
ASTs
Question: What do we assign behavior to?
Answer: The Abstract Syntax Tree (AST) of the program.
An AST is a data structure that represents a program.
A parser converts program text into an AST.
Question: How can we represent all while loops?
while (i < n && a[i] < x) { i++ }
Answer:
- Tag code as a while loop
- Identify the condition, which can be any expression
- Identify the body, which can be any expression
As a data structure:
- WHILEX(exp1, exp2), where
- exp1 is the representation of (i < n && a[i] < x), and
- exp2 is the representation of i++
Key question: names (review)
From ASTs to behaviors
28 January 2019: Judgments and Rules
There are PDF slides for 1/29/2019.
Students: Take a blank white card
Handout: Redacted Impcore rules
Today:
How do we know what happens when we run the code?
- Judgment
- Rules
- Valid derivations
What can we prove about it?
- Metatheory
Review: environments
Rules and metatheory
Review: What elements are needed to know run-time behavior?
OK, your turn: what do you think is rule for evaluating literal, variable? (Base cases)
Good and bad judgments
Proofs: Putting rules together
Every terminating computation is described by a data structure—we’re going to turn computation into a data structure: a tree. Proofs about computations are hard (see: COMP 170), but proofs about trees are lots easier (see: COMP 61).
Code example
(define and (p q)
(if p q 0))
(define digit? (n)
(and (<= 0 n) (< n 10)))Suppose we evaluate (digit? 7)
Exercise:
In the body of
digit?, what expressions are evaluated in what order?As a function application, the body matches template
(f e1 e2). In this example,- What is f?
- What is e1?
- What is e2?
Let’s develop the ApplyUser rule for the special case of two arguments: ⟨APPLY(f, e1, e2), ξ, ϕ, ρ⟩ ⇓ ?
What is the result of (digit? 7)?
How do we know it’s right?
From rules to proofs
Building a derivation
Building derivations
30 January 2019: Derivations, metatheory, better semantics
There are PDF slides for 1/31/2019.
Review: calls
Review: Derivations
Building a derivation
Building derivations
Proofs about derivations: metatheory
Cases to try:
- Literal
- GlobalVar
- SetGlobal
- IfTrue
- ApplyUser2
For your homework, “Theory Impcore” leaves out While and Begin rules.
4 February 2019: Scheme
There are PDF slides for 2/5/2019.
Announcements
Note: course not graded on a curve
Scheme homework:
- ramp-up
- not frightfully hard concepts, but…
- new language (notable load)
Where are we going?
Recursion and composition:
Recursive functions in depth
Two recursive data structures: the list and the S-expression
More powerful ways of putting functions together (compositionality again, and it leads to reuse)
Today: programming with lists and S-expressions (around laws)
For a new language, five powerful questions
As a lens for understanding, you can ask these questions about any language:
What is the abstract syntax? What are the syntactic categories, and what are the forms in each category?
What are the values? What do expressions/terms evaluate to?
What environments are there? That is, what can names stand for?
How are terms evaluated? What are the judgments? What are the evaluation rules?
What’s in the initial basis? Primitives and otherwise, what is built in?
(Initial basis for μScheme on page 159)
Introduction to Scheme
Two new kinds of data:
The function closure: the key to “first-class” functions
Pointer to automatically managed cons cell (mother of civilization)
Scheme Values
Most values are S-expressions.
An fully general S-expression is one of
a symbol
'Halligan'tuftsa literal integer
077a literal Boolean
#t#f(consv1 v2), where v1 and v2 are S-expressions
Many predefined functions work with a list of S-expressions
A list of S-expressions is either
the empty list
'()(consv vs), where v is an S-expression and vs is a list of S-expressionsWe say “an S-expression followed by a list of S-expressions”
Programming with lists and S-expressions
Lists: A subset of S-Expressions.
Can be defined via a recursion equation or by inference rules:
Constructors: '(),cons
Observers: null?, pair?, car, cdr (also known as “first” and “rest”, “head” and “tail”, and many other names)
Any list is therefore constructed with '() or with cons applied to an atom and a smaller list.
- How can you tell the difference between these types of lists?
- What, therefore, is the structure of a function that consumes a list?
Why are lists useful?
Sequences a frequently used abstraction
Can easily approximate a set
Can implement finite maps with association lists (aka dictionaries)
You don’t have to manage memory
These “cheap and cheerful” representations are less efficient than balanced search trees, but are very easy to implement and work with—see the book.
The only thing new here is automatic memory management. Everything else you could do in C. (You can have automatic memory management in C as well.)
Programming example: lists of numbers
Problem-solving: students pose problem on list of numbers
- Live coding: detect duplicate elements
μScheme’s new syntax
Immutable data structures
Key idea of functional programming: constructed data. Instead of mutating, construct a new one. Supports composition, backtracking, parallelism, shared state.
List-design shortcuts
Three forms of “followed by”
Given: Element .. list of values =
(cons x xs)Define: List of values .. list of values =
(append xs ys)Ignore: List of values .. element =
(snoc xs y)
Or(append xs (list1 y))
Two lists? Four cases!
Using informal math notation with .. for “followed by” and e for the empty sequence, we have these laws:
xs .. e = xs
e .. ys = ys
(z .. zs) .. ys = z .. (zs .. ys)
xs .. (y .. ys) = (xs .. y) .. ysThe underlying operations are append, cons, and snoc. Which ..’s are which?
But we have no
snocIf we cross out the
snoclaw, we are left with three cases… but case analysis on the first argument is complete.So cross out the law
xs .. e == xs.Which rules look useful for writing append?
You fill in these right-hand sides:
(append '() ys) ==
(append (cons z zs) ys) == Why does it terminate?
Cost model
The major cost center is cons because it corresponds to allocation.
How many cons cells are allocated?
Let’s rigorously explore the cost of append.
Induction Principle for List(A)
Suppose I can prove two things:
IH (’())
Whenever a in A and also IH(as), then IH (cons a as)
then I can conclude
Forall as in List(A), IH(as)
Claim: Cost (append xs ys) = (length xs)
Proof: By induction on the structure of xs.
Base case: xs = ’()
I am not allowed to make any assumptions.
(append '() ys) = { because xs is null } ysNothing has been allocated, cost is zero
(length xs)is also zero.Therefore, cost =
(length xs).
Inductive case: xs = (cons z zs)
I am allowed to assume the inductive hypothesis for
zs.Therefore, I may assume the number of cons cells allocated by
(append zs ys)equals(length zs)Now, the code:
(append (cons z zs) ys) = { because first argument is not null } = { because (car xs) = z } = { because (cdr xs) = zs } (cons z (append zs ys))The number of cons cells allocated is 1 + the number of cells allocated by
(append zs ys).cost of (append xs ys) = { reading the code } 1 + cost of (append zs ys) = { induction hypothesis } 1 + (length zs) = { algebraic law for length } (length (cons z zs)) = { definition of xs } (length xs)
Conclusion: Cost of append is linear in length of first argument.
Costs of list reversal
Algebraic laws for list reversal:
reverse '() = '()
reverse (x .. xs) = reverse xs .. reverse '(x) = reverse xs .. '(x)And the code?
The list1 function maps an atom x to the singleton list containing x.
How many cons cells are allocated? Let’s let n = |xs|.
- Q: How many calls to
reverse? A:n - Q: How many calls to
append? A:n - Q: How long a list is passed to
reverse? A:n-1,n-2, … ,0 - Q: How long a list is passed as first argument to
append? A:n-1,n-2, … ,0 - Q: How many
conscells are allocated by call tolist1? A: one per call toreverse. - Conclusion: O(n2) cons cells allocated. (We could prove it by induction.)
The method of accumulating parameters
Write laws for
(revapp xs ys) = (append (reverse xs) ys)Who could write the code?
The cost of this version is linear in the length of the list being reversed.
Parameter ys is the accumulating parameter.
(A powerful, general technique.)
Association lists represent finite maps (code not to be covered in class)
Implementation: list of key-value pairs
'((k1 v1) (k2 v2) ... (kn vn))Picture with spine of cons cells, car, cdar, caar, cadar.
Notes:
- attribute can be a list or any other value
- ‘nil’ stands for ‘not found’
Algebraic laws of association lists
6 Feb 2019: First-class and higher-order functions
There are PDF slides for 2/7/2019.
Skills refresh
Where we’ve been and where we’re going: Functional programming
Last time: new data forms (lists, S-expressions)
Today: New syntax, its rules and values
Context: Techniques and features we’re learning fit under functional programming.
- Idea: reuse more code because of “better glue”
Already doing it: immutable data (append)
- Always safe to share data (I can’t mess up things for you)
- Perfect for parallel/distributed (think Erlang)
- Perfect for web (JSON, XML)
Next up: better ways of gluing functions together
μScheme’s semantics
It’s not precisely true that rho never changes.
New variables are added when they come into scope.
Old variables are deleted when they go out of scope.
But the location associated with a variable never changes.
New syntax exploits semantics
Evaluate e1 through en, bind answers to x1, … xn
- Name intermediate results (simpler code, less error prone)
Creates new environment for local use only:
rho {x1 |-> v1, ..., xn |-> vn}
Also let* (one at a time) and letrec (local recursive functions)
Note that we would love to have definititions and it might be easier to read if McCarthy had actually used definition syntax, which you’ll see in ML, Haskell, and other functional languages:
So let’s see that semantics!
Key idea: don’t worry about memory
From Impcore to uScheme: Lambda
Anonymous, first-class functions
From Church’s lambda-calculus:
(lambda (x) (+ x x))“The function that maps x to x plus x”
At top level, like define. (Or more accurately, define is a synonym for lambda that also gives the lambda a name.)
In general, \x.E or (lambda (x) E)
xis bound inE- other variables are free in
E
The ability to “capture” free variables is what makes it interesting.
Functions become just like any other value.
First-class, nested functions
(lambda (x) (+ x y)) ; means what??What matters is that y can be a parameter or a let-bound variable of an enclosing function.
- Can tell at compile time what is captured.
- To understand why anyone cares, you’ll need examples
First example: Finding roots. Given n and k, find an x such that x^n = k.
Step 1: Write a function that computes x^n - k.
Step 2: Write a function that finds a zero between lo and hi bounds.
Picture of zero-finding function. Algorithm uses binary search over integer interval between lo and hi. Finds point in that interval in which function is closest to zero.
Code that computes the function x^n - k given n and k:
The function to-the-n-minus-k is a higher-order function because it returns another (escaping) function as a result.
General purpose zero-finder that works for any function f:
findzero-between is also a higher-order function because it takes another function as an argument. But nothing escapes; you can do this in C.
Example uses:
Your turn!!
How lambda works
Rule for lambda
Key idea: ``every name I can see—remember where it is stored.’’
Rule for function Application
Questions about ApplyClosure:
What if we used σ instead of σ0 in evaluation of e1?
What if we used σ instead of σ0 in evaluation of arguments?
What if we used ρc instead of ρ in evaluation of arguments?
What if we did not require ℓ1, ℓ2 ∉ dom(σ)?
What is the relationship between ρ and σ?
11 Feb 2019: Vocabulary building: List HOFs, the function factory
There are PDF slides for 2/12/2019.
Today: Using lambda to enlarge your vocabulary
- List computations
- Cheap functions from other functions
Similar: Haskell, ML, Python, JavaScript
Bonus: proving facts about functions
Higher-Order Functions on lists
Today: both functions and lists
Live coding interlude
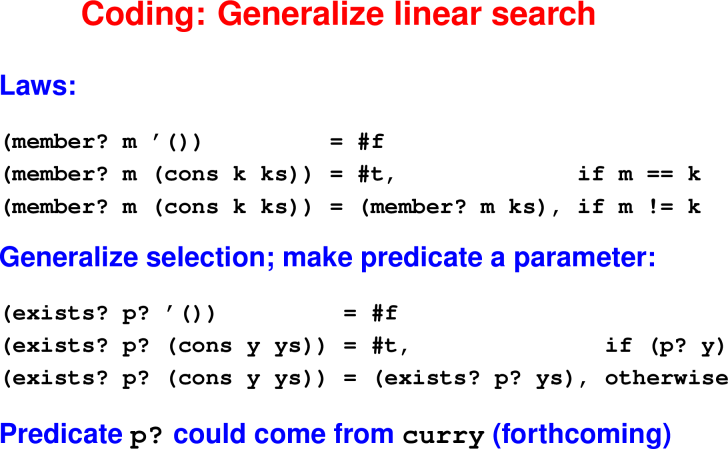
List search: exists?
Algorithm encapsulated: linear search
Example: Is there an even element in the list?
Algebraic laws:
(exists? p? '()) == ???
(exixts? p? '(cons a as)) == ???
(exists? p? '()) == #f
(exixts? p? '(cons a as)) == p? x or exists? p? xsList selection: filter
“Lifting” functions to lists: map
Algorithm encapsulated: Transform every element
Example: Square every element of a list.
Algebraic laws:
(map f '()) == ???
(map f (cons n ns)) == ???The universal list function: fold
foldr takes two arguments:
zero: What to do with the empty list.plus: How to combine next element with running results.
Example: foldr plus zero '(a b)
cons a (cons b '())
| | |
v v v
plus a (plus b zero)In-class exercise
Language design — why?
One-argument functions: Curry and compose
Build one-argument functions from two-argument functions
Currying converts a binary function f(x,y) to a function f' that takes x and returns a function f'' that takes y and returns the value f(x,y).
What is the benefit? Functions like exists?, all?, map, and filter all expect a function of one argument. To get there, we use Currying and partial application.
Curried functions take their arguments “one-at-a-time.”
Currying and list HOFs
One-argument functions compose
Preview: in math, what is the following equal to?
(f o g)(x) == ???Another algebraic law, another function:
(f o g) (x) = f(g(x))
(f o g) = \x. (f (g (x)))Another example: (o not null?)
13 Feb 2019: Tail calls and continuations
There are PDF slides for 2/14/2019.
Announcement: late homework
- 2, 3, 4 hours late == unfair
Announcement: recitations next week
- Thursday is Monday schedule, will have lecture
- Opportunity for make-up recitation Wednesday, Saturday
Where have we been, where are we going: functions
Today: proofs, costs, control flow
Proofs about functions
Tail calls
Intuition: In a function, a call is in tail position if it is the last thing the function does.
A tail call is a call in tail position.
Important for optimizations: Can change complexity class.
Anything in tail position is the last thing executed!
Key idea is tail-call optimization!
Example: reverse '(1 2)
Question: How much stack space is used by the call?
Call stack:
reverse '()
append
reverse '(2)
append
reverse '(1 2)Answer: Linear in the length of the list
Tail calls and the method of accumulating parameters
Trick: put answer in parameter
Write laws for
(revapp xs ys) = (append (reverse xs) ys)Who could write the code?
The cost of this version is linear in the length of the list being reversed.
Parameter ys is the accumulating parameter.
(A powerful, general technique.)
Example: revapp '(1 2) '()
Question: How much stack space is used by the call?
Call stack: (each line replaces previous one)
revapp ‘(1 2)’() –> revapp ‘(2)’(1) –> revapp ‘()’(2 1)
Answer: Constant
Answer: a goto!!
Think of “tail call” as “goto with arguments”
But goto is limited to labels named in the code.
Remember tail calls? Suppose you call a parameter!
A continuation is code that represents “the rest of the computation.”
- Not a normal function call because continuations never return
- Think “goto with arguments”
Continuations
Different coding styles
Direct style: Last action of a function is to return a value. (This style is what you are used to.)
Continuation-passing style (CPS): Last action of a function is to “throw” value to a continuation. For us, tail call to a parameter.
Uses of continuations
Compiler representation: Compilers for functional languages often convert direct-style user code to CPS because CPS matches control-flow of assembly.
Some languages provide a construct for capturing the current continuation and giving it a name
k. Control can be resumed at captured continuation by throwing tok.A style of coding that can mimic exceptions
Callbacks in GUI frameworks
Event loops in game programming and other concurrent settings
Even web services!
Implementation
We’re going to simulate continuations with function calls in tail position.
First-class continuations require compiler support: primitive function that materializes “current continuation” into a variable. (Missing chapter number 3.)
Motivating Example: From existence to witness
Ideas?
Bad choices:
- nil
- special symbol
'fail - run-time error
Good choice:
- exception (not in uScheme)
Question: How much stack space is used by the call?
Answer: Constant
20 Feb 2019: Continuations for backtracking
There are PDF slides for 2/21/2019.
Search demo
Continuations for Search
Solving a Literal
start carries a partial truth assignment to variables current
Box describes how to extend current to make a variable, say x, true.
Case 1: current(x) = #t
Call success continuation with current
Pass fail as resume continuation (argument to success)
Case 2: current(x) = #f
Call fail continuation
Case 3: x not in current
Call success continuation with current{x -> #t}
Pass fail as resume continuation
Board: pictures of two solvers:
- Make either A or B equal to
b(last time) [“or true”, “and false”] - Make both A and B equal to
b[“and true”, “or false”]
Solving a Negated Literal (Your turn)
start carries a partial truth assignment to variables current
Box describes how to extend current to make a negated variable, say not x, true.
Case 1: current(x) = #f
Call success continuation with current
Pass fail as resume continuation (argument to success)
Case 2: current(x) = #t
Call fail continuation
Case 3: x not in current
Call success cotinuation with current{x -> #f}
Pass fail as resume continuation
Solving A and B
Solver enters A
If A is solved, newly allocated success continuation starts B
If B succeeds, we’re done! Use
successcontinuation from context.If B fails, use
resumecontinuation A passed to B asfail.If A fails, the whole thing fails. Use
failcontinuation from context.
Solving A or B
Solver enters A
If A is solved, we’re good! But what if context doesn’t like solution? It can resume A using the resume continuation passed out as
fail.If A can’t be solved, don’t give up! Try a newly allocated failure continuation to start B.
If ever B is started, we’ve given up on A entirely. So B’s success and failure continuations are exactly the ones in the context.
If B succeeds, but the context doesn’t like the answer, the context can resume B.
If B fails, abject failure all around; call the original
failcontinuation.
Lisp and Scheme Retrospective
Common Lisp, Scheme
Advantages:
- High-level data structures
- Cheap, easy recursion
- Automatic memory management (garbage collection!)
- Programs as data!
- Hygenic macros for extending the language
- Big environments, tiny interpreters, everything between
- Sophisticated Interactive Development Environments
- Used in AI applications; ITA; Paul Graham’s company Viaweb
Down sides:
- Hard to talk about data
- Hard to detect errors at compile time
Bottom line: it’s all about lambda
- Major win
- Real implementation cost (heap allocation)
Bonus content: Scheme as it really is
- Macros!
- Cond expressions (solve nesting problem)
- Mutation
- …
Macros!
Conditional expressions
Mutation
21 Feb 2019: Introduction to ML
There are PDF slides for 2/22/2019.
Handout: Learning Standard ML
Ask the class: what are the strengths you found in μScheme programming? What are the pain points?
Apply your new knowledge in Standard ML:
- You’ve already learned (most of) the ideas
- There will be a lot of new detail
- Good language for implementing language features
- Good language for studying type systems
Meta: Not your typical introduction to a new language
- Not definition before use, as in a manual
- Not tutorial, as in Ullman
- Instead, the most important ideas that are most connected to your work up to now
ML Overview
Designed for programs, logic, symbolic data
Theme: Precise ways to describe data
ML = uScheme + pattern matching + static types + exceptions
ML forms of data
Live coding:
bool
string
int
list of int
list of bool
ill-typed list
pair
triple
functionMore live coding:
sum of list of int (fold)
reverse (with fold)Still more live coding? (New forms of data)
Ordinary S-expression
Binary tree of integersLive coding memories:
(* list selection *)
fun nth ([], 0) = raise Subscript
| nth (y :: ys, 0) = y
| nth ([], n) = raise Subscript
| nth (y :: ys, n) = nth (ys, n - 1)
(* better version: *)
fun nth ([], _) = raise Subscript
| nth (y :: ys, 0) = y
| nth (y :: ys, n) = nth (ys, n - 1)
(* binary trees of integers *)
datatype itree
= LEAF
| NODE of itree * int * itree
(* val root : itree -> int option *)
(* if tree is not empty, returns value at root *)
fun root LEAF = NONE
| root (NODE (left, n, right)) = SOME n
(* testing code *)
(* val singleton : int -> itree
`singleton n` returns tree with `n` as its only node *)
fun singleton n = NODE (LEAF, n, LEAF)
val t35 = NODE (singleton 3, 5, LEAF)
val () =
Unit.checkExpectWith (Unit.optionString Int.toString)
"root of t35"
(fn () => root t35) (SOME 5)μScheme to ML Rosetta stone
uScheme SML
(cons x xs) x :: xs
'() []
'() nil
(lambda (x) e) fn x => e
(lambda (x y z) e) fn (x, y, z) => e
|| && andalso orelse
(let* ([x e1]) e2) let val x = e1 in e2 end
(let* ([x1 e1] let val x1 = e1
[x2 e2] val x2 = e2
[x3 e3]) e) val x3 = e3
in e
endThree new ideas
- Pattern matching is big and important. You will like it. It’s “coding with algebraic laws”
- Exceptions are easy
- Static types get two to three weeks in their own right.
Pattern matching makes code look more like algebraic laws: one pattern for each case
Exceptions solve the problem “I can’t return anything sensible!”
Static types tell us at compile time what the cases are.
And lots of new concrete syntax!
Examples
The length function.
Algebraic laws:
length [] = 0 length (x::xs) = 1 + length xsThe code:
fun length [] = 0 | length (x::xs) = 1 + length xsThings to notice:
No brackets! (I hate the damn parentheses)
Function application by juxtaposition
Function application has higher precedence than any infix operator
Compiler checks all the cases (try in the interpreter)
Let’s try another! map, filter, exists, all, take, drop, takewhile, dropwhile
25 Feb 2019: Programming with constructed data and types
There are PDF slides for 2/26/2019.
Today’s lecture: lots of info in the notes, but won’t see in class. Because not everybody has a book.
Improving on Scheme
Foundation: Data
Syntax is always the presenting complaint, but data is what’s always important
- Base types:
int,real,bool,char,string - Functions
Constructed data:
- Tuples: pairs, triples, etc
- (Records with named fields)
- Lists and other algebraic types
Deconstruct using pattern matching
“Language support for forms of data”
“Distinguish one cons cell (or one record) from another”
Tuple types and arrow types
Background for datatype review (board):
if A and B are sets, what is
A * B?if A and B are sets, what is
A -> B?if A, B, and C are sets, what is
A * B * C?
This is all you need to know about the special built-in type constructors (cross and arrow).
Constructed data: Algebraic data types
Tidbits:
The most important idea in ML!
Originated with Hope (Burstall, MacQueen, Sannella), in the same lab as ML, at the same time (Edinburgh!)
Notes:
A “suit” is constructed using
HEARTS,DIAMONDS,CLUBS, orSPADESA “list of A” is constructed using
nilora :: as, whereais an A andasis a “list of A”A “heap of A” is either empty or it’s an A and two child heaps
Exegesis (on board):
Notation
'ais a type variable- On left-hand side, it is a formal type parameter
- On right-hand side it is an ordinary type
- In both cases it represents a single unknown type
Name before
=introduces a new type constructor into the type environment. Type constructors may be nullary.Alternatives separated by bars are value constructors of the type
They are new and hide previous names
(Do not hide built-in names
nilandlistfrom the initial basis!)Value constructors build constructed data
Value constructors participate in pattern matching
Complete by themselves:
HEARTS,SPADES,nilExpect parameters to make a value or pattern:
::,HEAP
Every
valon this slide is a value constructoropenables an infix operator to appear in a nonfix contextType application is postfix
- A list of integer lists is written:
int list list
- A list of integer lists is written:
New names into two environments:
suit,list,heapstand for new type constructorsHEARTS,CLUBS,nil,::,EHEAP,HEAPstand for new value constructors
Algebraic datatypes are inherently inductive (
listappears in its own definition)—to you, that means finite trees'a * 'a listis a pair type — infix operators are always applied to pairs
Your turn: S-expressions
The other form of constructed data: tuples
Additional language support for algebraic types: case expressions
Making types work for you
Types help me, part I: type-directed programming
Common idea in functional programming: "lifting:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)Potential bonus content: inorder traversal of binary tree.
val find : forall 'a . ('a -> bool) -> ('a list -> 'a option)Bonus content: Even more algebraic datatypes
Algebraic datatype review:
Enumerated types
Datatypes can define an enumerated type and associated values.
datatype suit = HEARTS | DIAMONDS | SPADES | CLUBSHere suit is the name of a new type.
The value constructors HEARTS, DIAMONDS, SPADES, and CLUBS are the values of type suit.
Value constructors are separated by vertical bars.
Pattern matching
Datatypes are deconstructed using pattern matching.
fun toString HEARTS = "hearts"
| toString DIAMONDS = "diamonds"
| toString SPADES = "spades"
| toString CLUBS = "clubs"
val suitName = toString HEARTSBut wait, there’s more: Value constructors can take arguments!
datatype int_tree = LEAF | NODE of int * int_tree * int_treeint_tree is the name of a new type.
There are two data constructors: LEAF and NODE.
NODEs take a tuple of three arguments: a value at the node, and left and right subtrees.
The keyword of separates the name of the data constructor and the type of its argument.
When fully applied, data constructors have the type of the defining datatype (ie, int_tree).
Building values with constructors
We build values of type int_tree using the associated constructors: (Draw on board)
val tempty = LEAF
val t1 = NODE (1, tempty, tempty)
val t2 = NODE (2, t1, t1)
val t3 = NODE (3, t2, t2)What is the in-order traversal of t3?
[1,2,1,3,1,2,1]What is the pre-order traversal of t3?
[3,2,1,1,2,1,1]Deconstruct values with pattern matching
(The @ symbol denotes append in ML)
fun inOrder LEAF = []
| inOrder (NODE (v, left, right)) =
inOrder left @ [v] @ inOrder right
val il3 = inOrder t3
fun preOrder LEAF = []
| preOrder (NODE (v, left, right)) =
v :: preOrder left @ preOrder right
val pl3 = inOrder t3int_tree is monomorphic because it has a single type.
Note though that the inOrder and preOrder functions only cared about the structure of the tree, not the payload value at each node.
But wait, there’s still more: Polymorphic datatypes!
Polymorphic datatypes are written using type variables that can be instantiated with any type.
datatype 'a tree = CHILD | PARENT of 'a * 'a tree * 'a treetree is a type constructor (written in post-fix notation), which means it produces a type when applied to a type argument.
Examples:
int treeis a tree of integersbool treeis a tree of booleanschar treeis a tree of charactersint list treeis a tree of a list of integers.
'a is a type variable: it can represent any type.
It is introduced on the left-hand of the = sign. References on the right-hand side are types.
CHILD and PARENT are value constructors.
CHILD takes no arguments, and so has type 'a tree
When given a value of type 'a and two 'a trees, PARENT produces a 'a tree
Constructors build tree values
val empty = CHILD
val tint1 = PARENT (1, empty, empty)
val tint2 = PARENT (2, tint1, tint1)
val tint3 = PARENT (3, tint2, tint2)
val tstr1 = PARENT ("a", empty, empty)
val tstr2 = PARENT ("b", tstr1, tstr1)
val tstr3 = PARENT ("c", tstr2, tstr2)Pattern matching deconstructs tree values
fun inOrder CHILD = []
| inOrder (PARENT (v, left, right)) =
(inOrder left) @ [v] @ (inOrder right)
fun preOrder CHILD = []
| preOrder (Parent (v, left, right)) =
v :: (preOrder left) @ (preOrder right)Functions inOrder and preOrder are polymorphic: they work on any value of type 'a tree. 'a is a type variable and can be replaced with any type.
Environments
Datatype definitions introduce names into:
the type environment:
suit,int_tree,treethe value environment:
HEART,LEAF,PARENT
Inductive
Datatype definitions inherently inductive:
the type
int_treeappears in its own definitionthe type
treeappears in its own definition
Datatype Exercise
Bonus content: Exceptions — Handling unusual circumstances
Syntax:
- Definition:
exception EmptyQueue - Introduction:
raise ewheree : exn - Elimination:
e1 handle pat => e2
Informal Semantics:
- alternative to normal termination
- can happen to any expression
- tied to function call
- if evaluation of body raises exn, call raises exn
Handler uses pattern matching
e handle pat1 => e1 | pat2 => e2
Bonus Content: ML traps and pitfalls
Bonus content (seen in examples)
Syntactic sugar for lists
Bonus content: ML from 10,000 feet
Environments
Patterns
Functions
Tuples are “usual and customary.”
Types
27 Feb 2019: Types
There are PDF slides for 2/28/2019.
Notes on slide:
- Guide: What have I got? What holes am I trying to fill?
Where type systems are found:
- C#, Swift, Go
- Java, Scala, Rust (polymorphism)
Trajectory:
- Formalize familiar, monomorphic type systems (like C)
- Learn polymorphic type systems
- Eventually, infer polymorphic types
Monomorphic types systems are the past.
Inference and polymorphism are the present and future.
(Visible trend just like lambda.)
Today:
- Type system with two types
- Type checking
- Unbounded number of types! (Formation, introduction, elimination)
- Revisiting “code from types” idea
Type systems
What kind of thing is it?
Questions type systems can answer:
What kind of value does it evaluate to (if it terminates)?
What is the contract of the function?
Is each function called with the right number of arguments?
(And similar errors)Who has the rights to look at it/change it?
Is the number miles or millimeters?
Questions type systems typically do not answer:
Can it divide by zero?
Can it access an array out of bounds?
Can it take the
carof'()?Will it terminate?
Type systems designed to solve a problem
- Confirm behavior
- Help the compiler
Type System and Checker for a Simple Language
Why do we write a type checker?
To be educated about programming languages, you must be able to realize inference rules in code. Eventually you should learn to “speak” inference rules like a native. Implementing a type system is a valuable way to build these competencies.
If (when!) you get to do your own language designs, type systems are an area where you are most likely to be able to innovate. The ideas behind type systems apply any time you need to validate user input, for example. This is the highest level of cognitive task: creation of new things.
Also your introduction to static analysis. Used in code improvement, security.
Define an AST for expressions with:
- Simple integer arithmetic operations
- Numeric comparisons
- Conditional
- Numeric literal
Examples to rule out
Can’t add a word and a flag:
3 + (3 < 99)
(ARITH(PLUS, LIT 3, CMP (LT, LIT 3, LIT 99)))Can’t compare a word and a flag
(3 < (4 = 24))
CMP (LT, LIT 3, CMP(EQ (LIT 4, LIT 24)))Inference rules to define a type system
Form of judgment Context
|-term:typeWritten
|- e : tauContexts vary between type systems
(Right now, the empty context)
Judgment is proved by derivation
Derivation made using inference rules
Inference rules determine how to code
val typeof : exp -> ty:Given e, find tau such that
|- e : tauWhat inference rules do you recommend for this language?
Rule for arithmetic operators
Informal example:
|- 3 : word |- 5 : word
-------------------------
|- 3 + 5 : wordRules out:
|- 'a' : char |- 5 : word
---------------------------
|- 'a' + 5 : ???General form:
|- e1 : word |- e2 : word
-----------------------------
|- ARITH ( _ , e1, e2) : wordRule for comparisons
Informal example:
|- 7 : word |- 10 : word
-----------------------------
|- 7 < 10 : flagGeneral form:
|- e1 : word |- e2 : word
-----------------------------
|- CMP ( _ , e1, e2) : flagRule for literals
Informal example:
|- 14 : wordGeneral form:
--------------------
|- LIT (n) : wordRule for conditionals:
Informal example:
|- true : flag
|- 3 : word
|- 42 : word
--------------------------
|- IF (true, 3, 42) : wordGeneral form:
|- e : flag
|- e1 : tau1
|- e2 : tau2 tau1 equiv tau2
-----------------------------------
|- IF ( e, e1, e2) : tau1Typing rules let us read off what a type checker needs to do.
input to checker: e
output from checker: tau
What types can rule out
things that could go wrong:
(8 < 10) + 4
(8 == 8) < 9
x + (x :: xs)
let val y = 10 in length y endWhat is a type?
Weak: a set of values
Better: a conservative prediction about values
Best: the precise definition: classifier for terms!!
The relationship to values becomes a proof obligation.
Note: a computation can have a type even if it doesn’t terminate! (Or doesn’t produce a value)
Source of new language ideas for next 20 years
Needed if you want to understand advanced designs (or create your own)
Type checker in ML
val typeof : exp -> ty
exception IllTyped
fun typeof (ARITH (_, e1, e2)) =
case (typeof e1, typeof e2)
of (WORDTY, WORDTY) => WORDTY
| _ => raise IllTyped
| typeof (CMP (_, e1, e2)) =
case (typeof e1, typeof e2)
of (WORDTY, WORDTY) => FLAGTY
| _ => raise IllTyped
| typeof (LIT _) = WORDTY
| typeof (IF (e,e1,e2)) =
case (typeof e, typeof e1, typeof e2)
of (FLAGTY, tau1, tau2) =>
if eqType (tau1, tau2)
then tau1 else raise IllTyped
| _ => raise IllTypedAn implementor’s trick: If you see identical types in a rule,
Give each type a distinct subscript
Introduce equality constraints
Remember to be careful using primitive equality to check types—you are better off with
eqType.
Typing Rules: Contexts and Term Variables
Your turn:
- What you need for VAR and LET
Things to think about:
Q: What context do we need to evaluate an expression?
Q: Do we need all the same context to decide on a type?
Q: What do we need then?
Rule for var
x in dom Gamma tau = Gamma(x)
----------------------------------------
Gamma |- VAR x : tauRule for let
Gamma |- e : tau
Gamma{x->tau} |- e' : tau'
-------------------------------------
Gamma |- LET x = e in e' : tau'What is the information flow?
Type Checker
Type checker needs Gamma – gives type of each “term variable”.
4 March 2019: Type checking with type constructors
There are PDF slides for 3/5/2019.
Type soundness
Approaching types as programmers
Talking type theory: Introduction and elimination constructs
Part of learning any new field: talk to people in their native vocabulary
Introduce means “produce”, “create”, “make”, “define”
Eliminate means “consume”, “examine”, “observe”, “use”, “mutate”
It’s like knowing what to say when somebody sneezes.
Review:
- Types classify terms
- Types serve a purpose (guide compiler, prevent bugs)
- Type system with two types
- Types relate to syntax (Introduction, Elimination)
- Typing rules
Upcoming (on the new homework)
- You will design new syntax and typing rules for lists
- You will extend an existing type checker
- You will implement a full type checker from scratch
This is a big chunk of what language designers do.
Functions
Introduction:
Gamma{x->tau1} |- e : tau2
-----------------------------------------
Gamma |- (lambda ([x : tau1]) e) : tau1 -> tau2Elimination:
Gamma |- e : tau1 -> tau2
Gamma |- e1 : tau1
-----------------------------
Gamma |- (e e1) : tau2Type Checking with Type Constructors
Type checking with type constructors
Formation, Introduction, and Elimination
Where we’ve been and where we’re going
New watershed in the homework
You’ve been developing and polishing programming skills: recursion, higher-order functions, using types to your advantage. But the problems have been mostly simple problems around simple data structures, mostly lists.
We’re now going to shift and spend the next several weeks doing real programming-languages stuff, starting with type systems.
You’ve already seen everything you need to know to implement a basic type checker, and you are almost fully equipped to add array operations and types to Typed Impcore.
What’s next is much more sophisticated type systems, with an infinite number of types. We’ll focus on two questions about type systems:
What is and is not a good type, that is, a classifier for terms?
How shall we represent types?
We’ll look at these questions in two contexts: monomorphic and polymorphic languages.
Design and implementation of monomorphic languages
Mechanisms:
Every new variety of type requires special syntax (examples: structs, pointers, arrays)
Implementation is a straightforward application of what you already know.
Language designer’s agenda:
What new types do I have (formation rules)?
What new syntax do I have to create new values with that type (introduction rules)?
For introduce think “produce”, “create”, “make”, “define”
What new syntax do I have to observe terms of a type (elimination rules)?
For eliminate think “consume”, “examine”, “interrogate”, “look inside”, or “take apart”, “observe”, “use”, “mutate”
Words “introduce” and “eliminate” are the native vocabulary of type-theoretic language design—it’s like knowing what to say when somebody sneezes.
Your turn: If I “add lists” to a language, how many new types am I introducing?
Managing the set of types: Type formation
Monomorphic type rules
Notice: one rule for if!!
Classic types for data structures
(At run time, identical to cons, car, cdr)
Typing Rule Exercise
Coding the arrow-introduction rule
6 March 2019: Polymorphic Type Checking; Kinds classify types
There are PDF slides for 3/7/2019.
Today
In class:
- Type-checking review
- Burdens of monomorphism
- On designers and implementors
- On programmers
- Lift burden with quantified types
- Extensible type formation
Language targets: Java, Scala, C# (with “generics”)
Typing Rule Exercise
Limitations of monomorphic type systems
Notes:
- Implementing arrays on homework
- Writing rules for lists on homework
Quantified types
Polymorphic Type Checking
Quantified types
Bonus instantiation:
-> map
<procedure> :
(forall ('a 'b)
(('a -> 'b) (list 'a) -> (list 'b)))
-> [@ map int bool]
<procedure> :
((int -> bool) (list int) -> (list bool))Two forms of abstraction:
Type rules for polymorphism
Type formation through kinds
Opening the closed world
Bonus content: a definition manipulates three environments
13 March 2019: Introduction to type inference
There are PDF slides for 3/14/2019.
Announcements
Recitation this week
Designed for final stages of homework. Your choice:
- Regression testing your type checker
- Coding in Typed uScheme (You could choose to hold off on problem TD.)
- Open office hours or AMA with your recitation leaders
Extra office hours
- Tomorrow
- Maybe Friday
- Week after break
(And you’ll get an email)
Today
How does the compiler know?
fun append (x::xs) ys = x :: append xs ys
| append [] ys = ysQuestions: where do explicit types appear in C?
Where do they appear in Typed μScheme?
Get rid of all that:
- Guess a type for each formal parameter
- Guess a return type
- Guess a type for each instantiation
Plan of study:
Today, I’ll walk through several examples, showing how to generate constraints
At end of class, you’ll do an example
After break, we’ll solve constraints
And for the next homework, you’ll implement both algorithms
Let’s do an example on the board
N.B. Book is “constraints first;” lecture will be “type system first.” Use whatever way works for you
(val-rec double (lambda (x) (+ x x)))What do we know?
doublehas type ′a1xhas type ′a2+has typeint * int -> int(+ x x)is an application, what does it require?- ′a2 =
intand ′a2 =int
- ′a2 =
Is this possible?
Key idea: Record the constraint in a typing judgement.
'a2 = int /\ 'a2 = int, { double : 'a1, x : 'a2 } |- (+ x x) : intExample: if
(if y 1 0)yhas type ′a3,1has typeint,0has typeintRequires what constraints? (
int=int, ′a3 = bool`)
Example:
(if z z (- 0 z))zhas type ′a3,0has typeint,-has typeint * int -> intRequires what constraints? (′a3 =
bool/\int=int/\′a3 =int)Is this possible?
Why not?
Inferring polymorphic types
(val app2 (lambda (f x y)
(begin
(f x)
(f y))))Assume f : ’a_f
Assume x : ’a_x
Assume y : ’a_y
f x implies ’a_f ~ (’a_x -> ’a)
f y implies ‘a_f ~ (’a_y -> ’a’)
Together, these constraints imply ‘a_x = ’a_y and ’a = ’a’
begin implies result of function is ’a
So,
app2 : (('a_x -> 'a) 'a_x 'a_x -> 'a)’a_x and ’a aren’t mentioned anywhere else in program, so
we can generalize to:
(forall ('a_x 'a) (('a_x -> 'a) 'a_x 'a_x -> 'a))which is the same thing as:
app2 : (forall ('a 'b) (('a -> 'b) 'a 'a -> 'b))25 March 2019: Making type inference precise
There are PDF slides for 3/26/2019.
Announcements
Office hours
This is the last week you can get full credit for a visit to my office hours. I am offering hours at these times:
- Today after class (booked, maybe some walk-ins)
- Tomorrow, March 26, 1:00 to 3:00 (booked, room for 9 walk-ins)
- Wednesday, March 27, 11:00 to 12:00 (booked, room for 4 walk-ins)
- Thursday, March 28, 11:00 to 12:00, 2:00 to 5:00 (many slots open)
- Friday, March 29, 11:00 to 12:00 (3 slots open, 4 walk-ins)
- Friday, March 29, 3:30 to 4:30 (1 slots open, 4 walk-ins)
Book a slot at https://www.cs.tufts.edu/~nr/cgi-bin/meeting.cgi?meeting=105.
Exam results:
What counts toward your final grade is your raw score. The nearest equivalent homework grade is shown as follows:
67 and up: Very Good (34 students)
50 to 67: Good (66 students)
29 to 50: Fair (17 students)
under 29: Poor ( 1 student)Review
Assume nss : ’b
We know car : forall ’a . ’a list -> ’a
=> car_1 : ’a1 list -> ’a1
=> car_2 : ’a2 list -> ’a2
(car_1 nss) => ’b ~ ’a1 list
(car_2 (car_1 nss)) => ’a1 ~ ’a2 list
(car_2 (car_1 nss)) : ’a2
nss : ’b
: 'a1 list
: ('a2 list) listSo, cc : (’a2 list) list -> ’a2
Because ’a2 is unconstrained, we can generalize:
cc : forall ’a . (’a2 list) list -> ’a
Bonus examples
Infer the type of function two:
Precise inference with Hindley-Milner types
To code the type-inference algorithm, replace eqType with constraint generation!
The inference algorithm, formally
Apply rule: e’s type could just be a type variable—we need to force it into the arrow form we need.
What you know and can do now
On the condition θΓ = Γ: Γ is “input”: it can’t be changed.
The condition ensures that θ doen’t conflict with Γ.
We can’t generalize over free type variables in Γ.
Their presence indicates they can be used somewhere else, and hence they aren’t free to be instantiated with any type.
27 March 2019: Building and using a constraint solver
There are PDF slides for 3/28/2019.
Announcement: exam hard copy (no markup), my office hours
Responses to midterm evals:
- Walk-in recitations Wednesdays 6pm
- 574 Boston Ave. rooms 310 and 316
- “Nobody goes there any more; it’s too crowded”
The queue:
It’s not meant to be first come, first served. Groups go before individuals.
Not everybody gets the same number of minutes. The goal is long-term fairness: everybody gets the help they need.
Break between homework releases: if I define a break, there are at least 20 students it works badly for. Define your own break.
We know we need to do better on proofs. Working on it for next year.
More to come
Today:
- Solving constraints
- Final inference rules:
- Generalize at VAL, LET, and LETREC
Solving constraints
What’s going on with substitutions? We have the informal idea—we just formalize it. It’s a function that behaves a certain way.
Two questions: what’s substitution, and when is a constraint satisfied?
Constraint satisfaction: equal types mean equal constructors applied to equal arguments—same is in eqType.
Solving simple type equalities
Question: in solving tau1 ~ tau2, how many potential cases are there to consider?
Question: how are you going to handle each case?
Solving conjunctions
Final pieces: completing the algorithm
Revisit a rule:
What you can know and do now
Write type inference for everything except VAL, VALREC, and LETX
Write function solve, which, given a constraint C, has one of three outcomes:
Returns the identity substitution in the case where C is trivially satisfied
Returns a non-trivial substitution if C is satisfiable otherwise.
Calls
unsatisfiableEqualityin when C cannot be satisfied
Instantiate and generalize
Moving from type scheme to types (Instantiation)
Moving from types to type scheme (Generalization)
From Type Scheme to Types
From Types to Type Scheme
The set A above will be useful when some variables in τ are mentioned in the environment.
We can’t generalize over those variables.
Applying idea to the type inferred for the function fst:
generalize(’a * ’b -> ’a, emptyset) = forall ’a, ’b. ’a * ’b -> ’a
Note the new judgement form above for type checking a declaration.
On the condition θΓ = Γ: Γ is “input”: it can’t be changed.
The condition ensures that θ doen’t conflict with Γ.
We can’t generalize over free type variables in Γ.
Their presence indicates they can be used somewhere else, and hence they aren’t free to be instantiated with any type.
Type Inference for Lets and Recursive Definitions
Let with constraints, operationally:
typesof: returns τ1, …, τn and Cval theta = solve CC-prime from
map,conjoinConstraints,dom,inter,freetyvarsGammafreetyvarsGamma,union,freetyvarsConstraintMap anonymous lambda using
generalize, get all the σiExtend the typing environment Gamma (pairfoldr)
Recursive call to type checker, gets
C_b,\tauReturn
(tau, C' /\ C_b)
Forall things
val and val-rec |
let, letrec, … |
lambda |
|---|---|---|
| FORALL contains all variables (because none are free in the context) | FORALL contains variables not free in the context | FORALL is empty |
| Generalize over all variables (because none are free in the context) | Generalize over variables not free in the context | Never generalize |
1 April 2019: Hiding information with abstract data types
There are PDF slides for 4/2/2019.
Handout: Mastering Multiprecision Arithmetic
Announcements
- Hiring TAs for fall
- https://www.cs.tufts.edu/~molay/compta
- Also Send an email to me or to Jeff Foster (next spring, next fall)
- Midterm course evals:
- Experimental Wednesday night recitation continues this week
- Photo is not deleted from server, but access is locked down. (Same policy as SIS.)
- Review of homework solutions: when??
- Exercises deemed redundant or repetitive; busy work: I may ask on Piazza (Note varied skills on recursion.)
- Questions in lecture: I’ll try to keep on point
- Moving images (soccer games and others): back row only
Plan for April:
- Programming at scale: modules and objects
- Lambda calculus (connections to modules and to Smalltalk)
Today’s learning objectives:
- Ideas found in language designs
- Terminology
- Understanding interfaces in Standard ML
Data abstraction
Where have we been?
- Programming in the small
- Expressive power
Success stories:
- First-class functions
- Algebraic data types and pattern matching
- Polymorphic type systems
What about big programs?
- Immersion in pile of interpreter code: not fun
An area of agreement and a great divide:
INFORMATION HIDING
(especially: mutable data)
/ \
/ \
modular reasoning / \ code reuse
/ \
internal access / \ interoperability
to rep / \ between reps
/ \
MODULES OBJECTS
ABSTRACT TYPESWhy modules?
Unlocking the final door for building large software systems
You have all gotten good at first-class functions, algebraic data types, and polymorphic types
Modules are the last tool you need to build big systems
Modules overview
Functions of a true module system:
Hide representations, implementations, private names
“Firewall” separately compiled units (promote independent compilation)
Possibly reuse units
Real modules include separately compilable interfaces and implementations
Designers almost always choose static type checking, which should be “modular” (i.e., independent)
C and C++ are cheap imitations
- C doesn’t provide namespaces
- C++ doesn’t provide modular type checking for templates
Interfaces
Collect declarations
- Unlike definition, provides partial information about a name (usually environment and type)
Things typically declared:
Variables or constants (values, mutable or immutable)
Types
Procedures (if different from values)
Exceptions
Key idea: a declared type can be abstract
- Just like a primitive type
Terminology: a module is a client of the interfaces it depends on
Roles of interfaces in programming:
The unit of sharing and reuse
Explainer of libraries
Underlie component technology
The best-proven technology for structuring large systems.
Ways of thinking about interfaces
Means of hiding information (ask “what secret does it hide?”)
A way to limit what we have to understand about a program
- Estimated force multiplier x10
A contract between programmers
- Essential for large systems
- Parties might be you and your future self
Interface is the specification or contract that a module implements
- Includes contracts for all declared functions
Module Implementations
Holds all dynamically executed code (expressions/statements)
May include private names
May depend only on interfaces, or on interfaces and implementations both (max cognitive benefits when all dependency is mediated by interfaces)
Dependencies may be implicit or explicit (
import,require,use)
Standard ML Modules
The Perl of module languages?
Has all known features
Supports all known styles
Rejoice at the expressive power
Weep at the terminology, the redundancy, the bad design decisions
What we’ve been using so far is the core language
Modules are a separate language layered on top.
Signature basics
ML Modules examples, part I
3 April 2019: more ML modules
There are PDF slides for 4/4/2019.
Abstract data types
Data abstraction for reuse
Functors and an Extended SML Example
Extended example: Error-tracking Interpreter
Why this example?
Lots of interfaces using ML signatures
Idea of how to compose large systems
Some ambitious, very abstract abstractions—it’s toward the end of term, and you should see something ambitious.
Practice implementing functors
Error modules: Three common implementations
Collect all errors
Keep just the first error
Keep the most severe error
Your obligations: two types, three functions, algebraic laws
Computations Abstraction
Ambitious! (will make your head hurt a bit)
Computations either:
return a value
produce an error
Errors must be threaded through everything :-(
That’s really painful!
We can extend the computation abstraction with sequencing operations to help.
Example:
eval e1 + eval e2
(op +) (eval e1, eval e2)
curry (op +) (eval e1) (eval e2)
curry (op +) <$> eval e1 <*> eval e2The first three versions are not well typed. Why?
The last version will thread errors through the compuation behind the scenes.
Note:
eval e1, eval e2 : int comp
curry (op +) : int -> (int -> int)
<$> : (int -> (int -> int)) * (int comp) -> (int -> int) comp
<*> : (int -> int) comp * int comp -> int comp
curry (op +) <$> eval e1 : (int -> int) comp
let pa = curry (op +) <$> eval e1
note by above, pa : (int -> int) comp
pa <*> eval e2 : int compML Module summary
8 April 2019: Lambda Calculus
There are PDF slides for 4/9/2019.
Handouts:
Calculus examples:
| Concurrency | CCS (Robin Milner) |
| Security | Ambient calculus (Cardelli and Gordon) |
| Distributed computing | pi calculus (Milner) |
| Biological networks | stochastic pi calculus (Regev) |
| Computation | lambda calculus (Church) |
Substitution examples:
- bash
- tcl/tk
- TeX/LaTeX
What is a calculus?
Demonstration of differential calculus: reduce
d/dx (x + y)2
Rules:
d/dx k = 0
d/dx x = 1
d/dx y = 0 where y is different from x
d/dx (u + v) = d/dx u + d/dx v
d/dx (u * v) = u * d/dx v + v * d/dx u
d/dx (e^n) = n * e^(n-1) * d/dx eSo
d/dx (x + y)2
2 ⋅ (x + y) ⋅ d/dx(x + y)
2 ⋅ (x + y) ⋅ (d/dxx + d/dxy)
2 ⋅ (x + y) ⋅ (1 + d/dxy)
2 ⋅ (x + y) ⋅ (1 + 0)
2 ⋅ (x + y) ⋅ 1
2 ⋅ (x + y)
What is a calculus? Manipulation of syntax.
What corresponds to evaluation? “Reduction to normal form”
Why study lambda calculus?
A metalanguage for describing other languages, known to all educated people
(Church-Turing Thesis: Any computable operator can be encoded in lambda calculus)
Test bench for new language features
Theoretical underpinnings for most programming languages (all in this class).
The world’s simplest reasonable programming language
Just application, abstraction, variables
- Living without
let,while - Living without
if - Living without recursive
define - Coding data structures
- Coding natural numbers
Only three syntactic forms:
M ::= x | \x.M | M M'Everything is programming with functions
Everything is Curried
Application associates to the left
Arguments are not evaluated
First example:
(\x.\y.x) M N --> (\y.M) N --> MCrucial: argument N is never evaluated (could have an infinite loop)
Programming in Lambda Calculus
Absolute minimum of code forms: no set, while, begin, but also no if and no define!
Alert to the reading: Wikipedia is reasonably good on this topic
EXCEPT for the way they encode lists, which is bogus (violates abstraction)
Instead, use my handout “Coding in Lambda Calculus”
Systematic approach to constructed data:
Everything is continuation-passing style
Q: Who remembers the boolean-formula solver?
Q: What classes of results could it produce?
Q: How were the results delivered?
Q: How shall we do Booleans?
Coding Booleans and if expressions
A Boolean takes two continuations.
Laws:
true s f = s
false s f = fCode:
true = \x.\y.x
false = \x.\y.yCoding the if expression, laws:
if true then N else P = N
if false then N else P = PTherefore, code is:
if M then N else P = ???Your turn: implement not
Laws for
not: what are the forms of the input data?Code for
not
Coding data structures
Coding pairs
If you have a pair containing a name and a type, how many alternatives are there?
How many continuations?
What information does each expect?
What are the algebraic laws?
fst (pair x y) = x snd (pair x y) = yCode
pair,fst,sndpair x y k = k x y fst p = p (\x.\y.x) snd p = p (\x.\y.y) pair = \x.\y.\f.f x y fst = \p.p (\x.\y.x) snd = \p.p (\x.\y.y)
Coding lists
List laws
null? nil = true null? (cons x xs) = false car (cons x xs) = x cdr (cons x xs) = xsHow many ways can lists be created?
How many continuations?
What does each continuation expect?
For each creator, what are the laws regarding its continuations?
cons y ys n c = c y ys nil n c = n car xs = xs error (\y.\ys.y) cdr xs = xs error (\y.\ys.ys) null? xs = xs true (\y.\ys.false)What are the definitions?
cons = \y.\ys.\n.\c.c y ys nil = \n.\c.n car = \xs.xs error (\y.\ys.y) cdr = \xs.xs error (\y.\ys.ys) null? = \xs.xs true (\y.\ys.false)What do those second continuations look like? (This is the source of Wikipedia’s terrible hack)
Coding numbers: Church Numerals
Operational semantics of lambda calculus
New kind of semantics: small-step
New judgment form
M --> N ("M reduces to N in one step")No context!! No turnstile!!
Just pushing terms around == calculus
Normal forms
10 April 2019: Lambda-calculus semantics; encoding recursion
There are PDF slides for 4/11/2019.
Today
Lambda:
- Operational semantics
- Beta reduction and capture-avoiding substitution
- Reduction strategies (making deterministic)
- Recursion and the Y combinator
Review: Church encodings
Question: What’s missing from this picture?
Answer: We’re missing recursive functions.
Astonishing fact: we don’t need letrec or val-rec (to com)
To see how it works, first, the semantics
Beta-reduction (homework, part 2)
The substitution in the beta rule is the heart of the lambda calculus
- It’s hard to get right
- It’s a stupid design for real programming (shell, tex, tcl)
- It’s even hard for theorists!
- But it’s the simplest known thing
Board examples:
Are these functions the same?
\x.\y.x \w.\z.wAre these functions the same?
\x.\y.z \w.\z.z
Examples of free variables:
\x . + x y
\x. \y. xExample:
(\yes.\no.yes)(\time.no) ->
\z.\time.noand never
\no.\time.no // WRONG!!!!!!Really wrong!
(\yes.\no.yes) (\time.no) tuesday
-> WRONG!!!
(\no.\time.no) tuesday
->
\time.tuesdayMust rename the bound variable:
(\yes.\no.yes) (\time.no) tuesday
->
(\yes.\z.yes) (\time.no) tuesday
->
(\z.\time.no) tuesday
->
\time.noNondeterminism of conversion:
A
/ \
V V
B CNow what??
Reduction strategies (your homework, part 2)
Applicative-order reduction
Given a beta-redex
(\x.M) Ndo the beta-reduction only if N is in normal form
- Good model for ML and Scheme, so-called “call by value” languages
- Think “arguments before bodies”
Q: Does applicative order ever prevent you from making progress?
A: No. We can prove it by induction on the number of lambdas in N
Normal-order reduction
Always choose leftmost, outermost redex
Normalization theorem: if a normal form exists, this will find it
Model for Haskell, Clean
You can try ‘uhaskell’, but if it does anything useful, we’re all surprised and pleased
“Normal-order” stands for produces a normal form, not for “the normal way of doing things”
Not your typical call-by-value semantics!
Coding recursion
Using fixed points
Now you do it
Lambda calculus in context
What’s its role in the world of theory?
Operational semantics Type theory Denotational Lambda
(Natural deducation style) semantics calculus
-------------------------- ----------- ------------ --------
Interpreters like Python type checkers compilers *models*Why is it “calculus”?
Differential calculus example: d/dx x^n equals what?
What’s going on here?
Answer: pure formal manipulation
No understanding of functions required; you could write a program to do it (and many people have)
What’s the role of calculi in computer science:
Lambda calculus:
A metalanguage for describing other languages
A starter kit for experimenting with new features
Process calculus:
Concurrent and parallel programming
Biological processes!
Pi calculus:
- Mobile computing and mobile agents
Ambient calculus:
- Security and protection domains
Why so many calculi? They have simple metatheory and proof technique.
17 April 2019: Object-orientation
There are PDF slides for 4/18/2019.
Languages: JavaScript, Ruby, Java, C++, Python, …
What it’s about:
- Encapsulation
- Higher-order programming
- Dynamic dispatch
- (Inheritance)
In common with modules, lambda calculus: you can’t touch things directly.
Object-oriented demo
Demo: circle, square, triangle, with these methods:
position:cardinal-pointset-position:to:cardinal-point coordinatedraw
Instructions to student volunteers
- You have one instance variable, which is a coordinate position.
Messages:
Object 1, adjust your coordinate to place your South control point at (0, 0).
Object 1, what is the coordinate position of your North control point?
Object 2, adjust your coordinate to place your South control point at (0, 2).
Object 2, what is the coordinate position of your North control point?
Object 3, adjust your coordinate to place your Southwest control point at (0, 4).
Object 1, draw yourself on the board
Object 2, draw yourself on the board
Object 3, draw yourself on the board
Key concepts of object-orientation
Key mechanisms
Encapsulate: Private instance variables
- Only object knows its instance variables and can see them
- C++ calls these “members”
- Like the coordinate of the geometric figure
- (This is the information hiding)
Higher-order: Code attached to objects and classes
- Code needed to draw the object is associated with the object
(A species of higher-order programming)
Dynamic dispatch (NEW)
- We don’t know what function will be called
- In fact, there is no function; code is a ``method’’
Key idea
Protocol determines behavioral subtyping
Class-based object-orientation
Dynamic dispatch determined by class definition
Code reuse by sending messages around like crazy
What’s hard
- Encapsulation: abstraction function and invariant
- Higher-order programming: everything is higher order
- Dynamic dispatch: every call is to an unknown function (trust the contract)
- Inheritance: big vocabulary, hard to work one function in isolation
Net effect: algorithms “smeared out” over many methods
What’s great
- Cooperating-objects model
- Reuse, reuse, reuse
Example: list filter
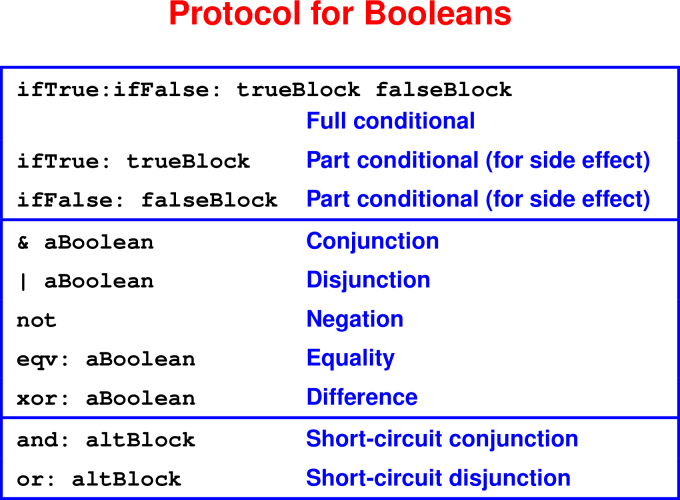
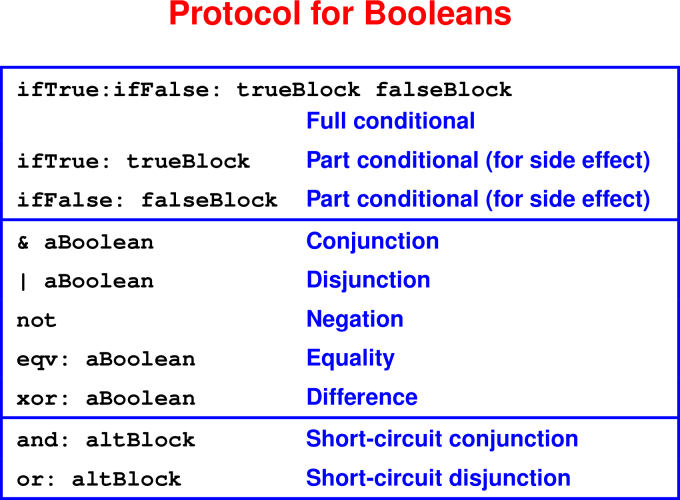
Blocks and Booleans
[block (formals) expressions]For parameterless blocks (normally continuations),
{expressions}
Blocks are objects
- You don’t “apply” a block; you “send it the
valuemessage”
Booleans use continuation-passing style
- Blocks delay evaluation
Booleans implemented with two classes True and False
- one value apiece
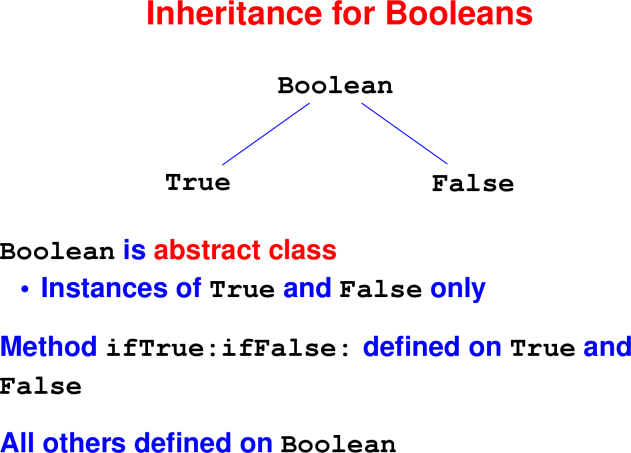
Method dispatch in the Booleans
Board - Method dispatch
To answer a message:
Consider the class of the receiver
Is the method with that name defined?
If so, use it
If not, repeat with the superclass
Run out of superclasses?
“Message not understood”
22 April 2019: Inheritance. Dispatch. Numbers and magnitudes
There are PDF slides for 4/23/2019.
White cards: AMA (emphasize programming languages past, present, and future)
Final course evaluations:
- Submit screen shot
- Also recitation-leader survey: https://forms.gle/ivtyGX25B3iCcZbp7
- Submit
course.pngandrecitation.pngusingsubmit105-evals
Plan for the week
Object-oriented mechanisms
Key mechanisms
- Dynamic dispatch
- Private instance variables
Object-oriented design
Key ideas (today, context for understanding, start h/w):
- Big protocols on small foundations
- Two roles of classes
Key ideas (next time, build on today):
- Power of dynamic dispatch
- Behavioral subtyping (“duck typing”, protocols)
Case studies related to the homework.
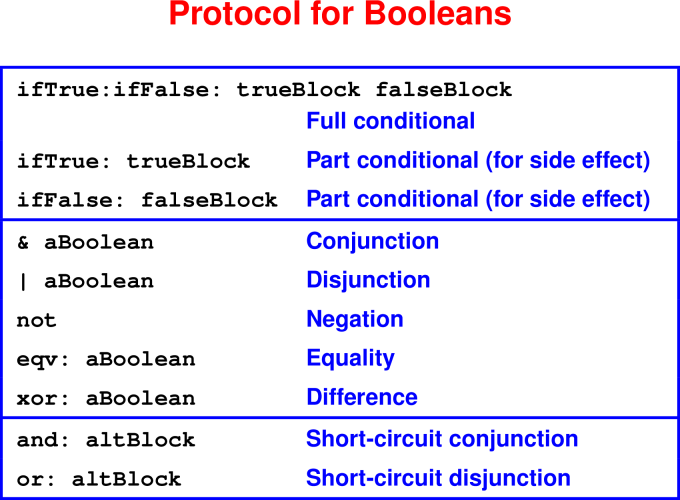
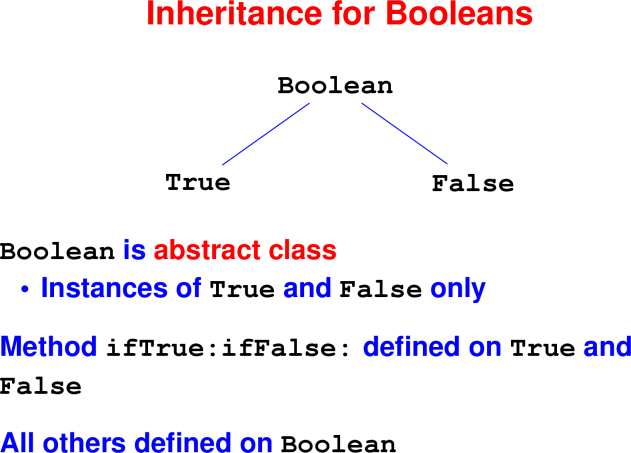
Method dispatch in the Booleans
Booleans implemented with two classes True and False
- one value apiece
Board - Method dispatch
To answer a message:
Consider the class of the receiver
Is the method with that name defined?
If so, use it
If not, repeat with the superclass
Run out of superclasses?
“Message not understood”
Smalltalk syntax and values
Values first:
Every value is an object.
Every class is an object!
Message passing:
Look at SEND
- Message identified by name (messages are not values)
- Always sent to a receiver
- Optional arguments must match arity of message name
(no other static checking)
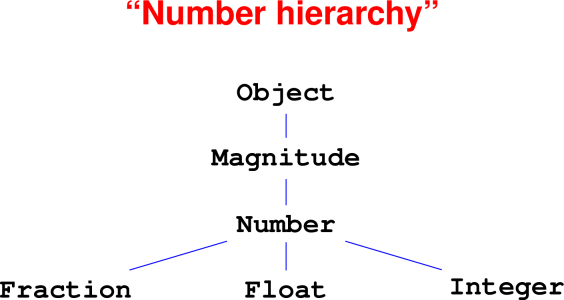
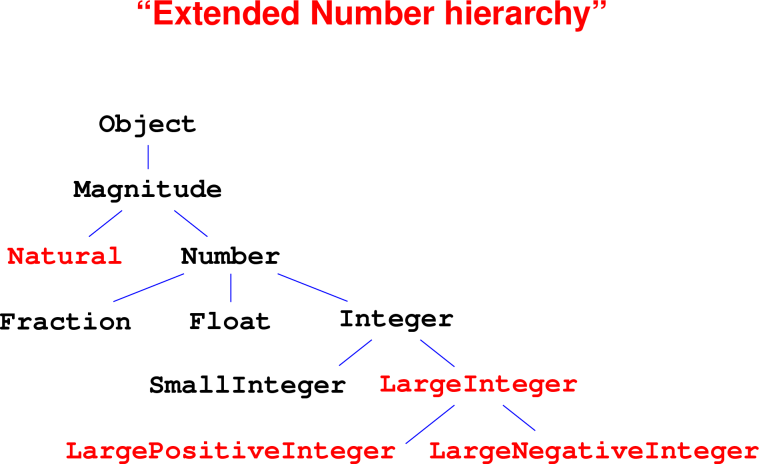
Case study: Magnitudes and numbers
Key problems on homework
Naturalis aMagnitude“Large integer” is a
Number
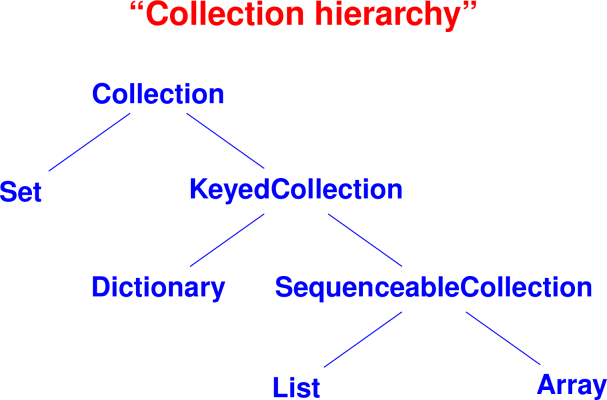
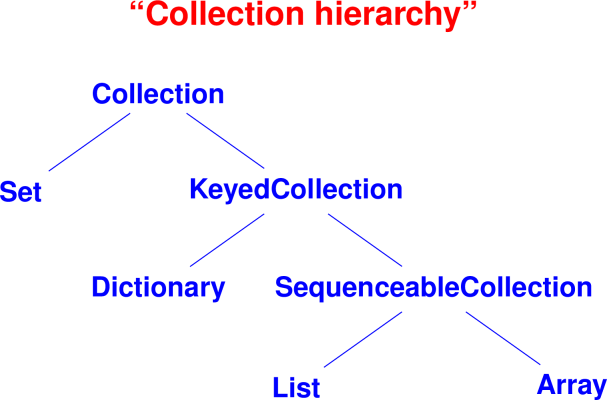
Bonus case study not covered in class: Collections
Why collections?
Goal of objects is reuse
Key to successful reuse is a well-designed class hierarchy
Killer app: toolkits for building user interfaces
Smalltalk blue book is 90 pages on language, 300 pages on library
Lots of abstract classes
- Define protocols
- Build reusable stuff, just like
Boolean,Magnitude,Number
Implementing Collections
Question: what’s the most efficient way to find the size of a list?
Question: what’s the most efficient way to find the size of an array?
24 April 2019: Double dispatch, collections
There are PDF slides for 4/25/2019.
More AMA’s
COURSE EVALUATIONS: upload a screen shot
Advertising: COMP 150 PLD (small class!)
- Programming-language design
Two topics for today
Initialization and invariants
Information hidden and revealed; three layers
(Focus on extending open systems)
Initialization and invariants
Making open system extensible
Bonus: Subtyping
Key strategy for reuse in object-oriented languages: subtype polymorphism
A value of the subtype can be used wherever a value of the supertype is expected.
Board:
- SUBTYPE != SUBCLASS
- SUPERTYPE != SUPERCLASS
Only crippled languages like C++ identify subtype with subclass
Only the ignorant and uneducated don’t know the difference
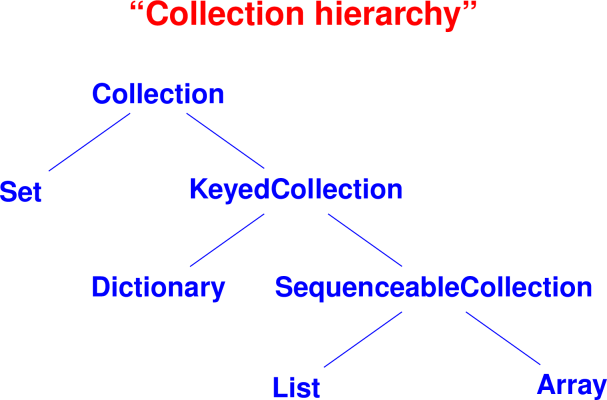
Bonus case study not covered in class: Collections
Why collections?
Goal of objects is reuse
Key to successful reuse is a well-designed class hierarchy
Killer app: toolkits for building user interfaces
Smalltalk blue book is 90 pages on language, 300 pages on library
Lots of abstract classes
- Define protocols
- Build reusable stuff, just like
Boolean,Magnitude,Number
Implementing Collections
Question: what’s the most efficient way to find the size of a list?
Question: what’s the most efficient way to find the size of an array?
Example collection - Sets
Most subclass methods work by delegating all or part of work to list members
N.B. Set is a client of List, not a subclass!
Next example highlight: class method and super!