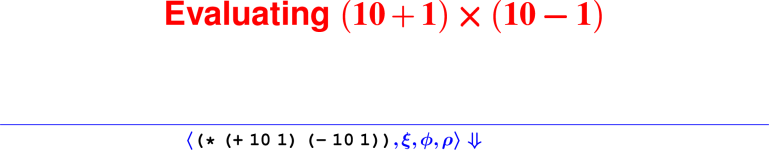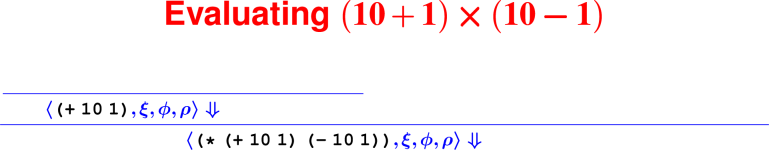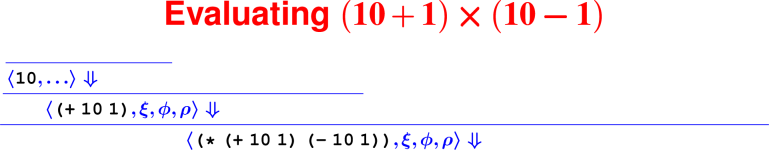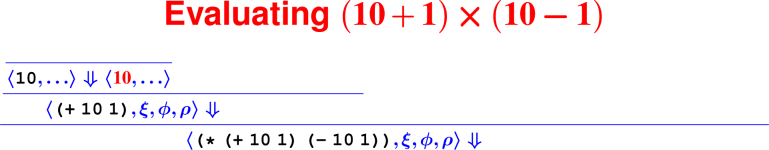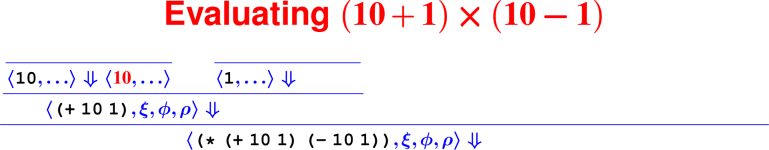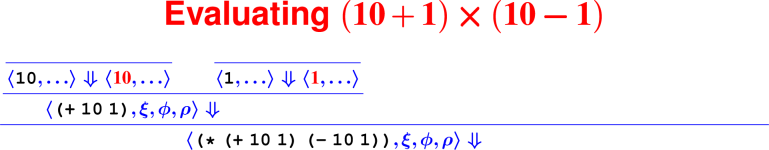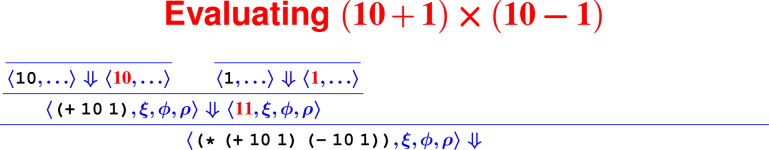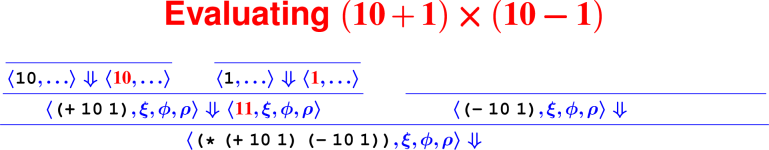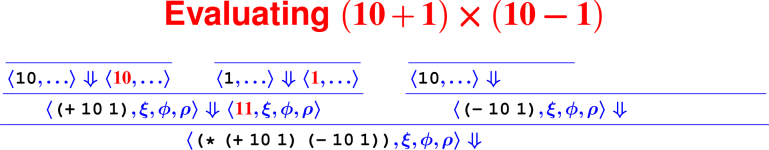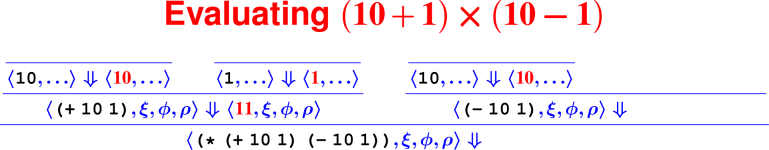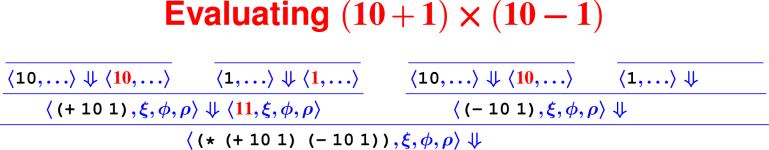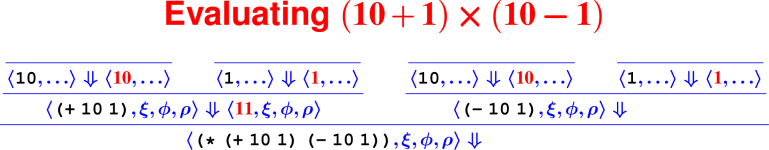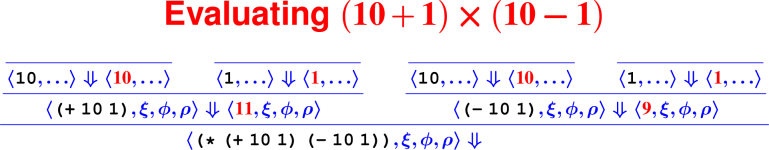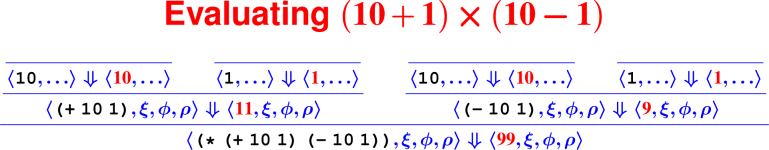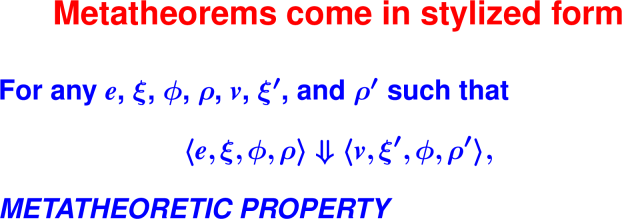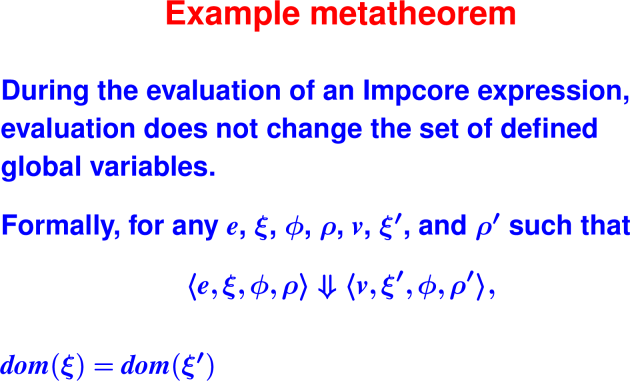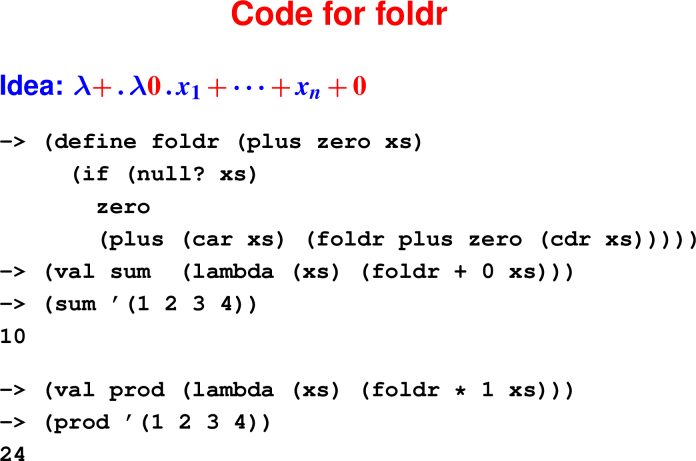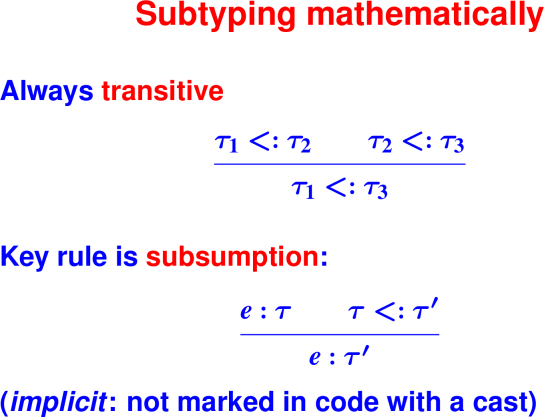9 September 2020: Introduction to Comp 105
There are PDF slides for 9/10/2020.
Handout: Experiences of successful 105 students
Handout: Lessons in program design
Introduction
My pronouns are she, her, hers.
Please call me “Kathleen,” or “Professor Fisher”
Reflection: Are all programming languages created equal?
Under what circumstances is one programming language better than another one? Write 2-3 sentences explaining your thoughts.
Why we are here
- Write code from scratch
- In a language you’ve never seen
- That sails past code review
Why it’s different from COMP 40:
- Machines haven’t really changed since 1970 (mainframes), 1980 (minicomputers), 1982 (microcomputers)
- Languages are changing all the time
What it involves:
- Programming practice (emphasize widely used features: functions, types, modules, objects)
- Mathematical description (how things work, see patterns)
(Example: see patterns of recursion in homework)
Today:
- Start with technical work
- Then a little about experience and expectations
What is a programming language?
What is a PL?
If you’ve taken 170, a caution: every programming language is a formal language, but not every formal language is a programming language.
My answer: a language with a compositional structure that has an element of run time to it.
Key idea: phase distinction
Something you write down, which just sits there
Something that runs
We will talk about “compile time” and “run time” (and later, type-checking time).
Key ideas: static and dynamic
The thing that you write down is syntax
What flies around at run time is values
(You know about syntax and values already—but this semester we’re going to think about them very systematically.
First three classes: new ways of thinking about stuff you already know
Check your understanding: The big picture
- The goal of this course is to teach you principles of programming languages so you’ll be able to teach yourself new languages quickly and improve your coding in many different languages.
- True
- False
- Almost all languages are equally powerful, and so are equally well suited to solving any programming task.
- True
- False
Check your understanding: Syntax vs. semantics
Indicate whether each statement is more about the syntax or the semantics of a program:
- A valid C program always has a matching
}for every{.
- syntax
- semantics
- A valid C program never dereferences an uninitialized pointer.
- syntax
- semantics
- In a valid C program, the right-hand side of an
=operation must be an expression.
- syntax
- semantics
- In our house style, every
ifstatement has a correspondingelse.
- syntax
- semantics
- When a ternary conditional expression
x ? y : zis evaluated, it acts a lot like anif
- syntax
- semantics
Reflection: Inductive definitions for numerals
Numerals are an example of syntax: the rules for how things are written. At run time, a numeral stands for a natural number; the natural number is its semantics. Numerals are things like 0, 2020, 73, and 1852.
They are not things like 311t3, 2+2, or -12.
Write an inductive definition of numerals (think base case and inductive case).
There’s more than one! When you finish, look for another.
Value structure for numerals: Induction
Example: Numerals
Numerals are syntax; Natural numbers are semantics
Numerals:
2018
73
1852Not numerals:
3l1t3
2+2
-12Approach 1: the cons approach
- if
dis a digit thendis a numeral - if
dis a digit andnis a numeral thendnis a numeral
Approach 2: the snoc approach
- if
dis a digit thendis a numeral - if
dis a digit andnis a numeral thenndis a numeral
Approach 3: the tree approach
- if
dis a digit thendis a numeral - if
n1is a numeral andn2is a numeral thenn1 n2is a numeral
have written a list or sequence of digits as a definition. That’s good thinking, but it leaves open the problem of defining “list” or “sequence”. These definitions take care of that issue.
Check your understanding: Representations of numerals
Different representations make different operations easier. Consider the three different ways we discussed to represent numerals, which we called the cons, snoc, and tree approaches.
- Which representation makes it easiest to access the most significant digit?
conssnoctree
- Which representation makes it easiest to access the least significant digit?
conssnoctree
- Which representation makes it equally easy to access either the first or last digit?
conssnoctree
Reflection: Natural numbers
We have limited operations on numerals: stick a digit before or after a numeral, or stick two numerals together. But on numbers we have many more operations. What are two simple, useful operations that are defined on natural numbers?
Value structure for natural numbers: induction again
Natural numbers are semantics for numerals.
Infinite set, that we’ll define using induction.
- Base case: a
digitis anat - Inductive case: if
mis anatanddis adigitthen10*m + dis anat
Check your understanding: Representations of numerals
The decimal definition of natural numbers in the video ignores almost all operations on natural numbers. It uses just addition and multiplication. And not just any addition and multiplication, but a highly stylized one: multiply by ten and then add. So out of all the gazillions of ways we might compute a natural number, we are limiting ourselves. According to this definition, how many different ways of forming natural numbers must we consider to be able to account for every natural number?
- one
- two
- ten
- gazillions
- infinite
Reflection: Defining functions over natural numbers
We want to define a function that examines a natural number (actually a machine integer) to find out if its numeral can written using only the digit 4. How many cases will such a function have to consider? Do any of the cases look like they will require recursion?
Writing code with recursion and induction
Data-driven design process. Connections to design ideas from 1970s, 1980s, 1990s, plus test-driven development (2000s).
Check your understanding: Design process
Put the nine steps of the design process for writing functions guided by the structure of the data and algebraic laws in order.
- Turn right-hand sides of algebraic laws into results
- Specify example results
- Choose function’s name
- Revisit Tests
- Describe function’s contract
- List example inputs
- Choose representation of inputs
- Turn left-hand sides of algebraic laws into case analysis
- Write algebraic laws
The all-fours? function
;; forms of data
;; Either a single digit d
;; OR 10 * m + d where m not equal 0
;; example inputs
(val x1 4 )
(val x2 9)
(val x3 44)
(val x4 907)
(val x5 48)
;; Pick the name now
;; Write the contract now
;; Write check assert cases now
;; Algebraic Laws
;; (all-fours? d) = (= d 4)
;; (all-fours? (+ (* 10 m) d)) ==
;; (= d 4) && (all-fours? m)
;; The code!
;; return nonzero if and only if
;; decimal rep of n can be written
;; using only the digit 4
(define all-fours? (n)
(if (< n 10)
(= n 4)
(and (= 4 (mod n 10))
(all-fours? (/ n 10)))))
(check-assert (all-fours? 4))
(check-assert (not (all-fours? 9)))
(check-assert (all-fours? 44))
(check-assert (not (all-fours? 48)))
(check-assert (not (all-fours? 907)))
Coding Interlude: all-fours?
Consider the all-fours? code from the previous video. Run the code on the sample data.
Change the code to make it be the all-nines? function.
Reflection: Various syntactic forms
Consider the following two functions that show all the syntactic forms in Impcore.
(define even? (n) (= (mod n 2) 0))
(define 3n+1-sequence (n) ; from Collatz
(begin
(while (!= n 1)
(begin
(println n)
(if (even? n)
(set n (/ n 2))
(set n (+ (* 3 n) 1)))))
n))What do you think these functions do?
What do you notice about the syntax of these functions (ie, how they are written down)?
How might you write these same two functions in C?
Syntax in programming languages
14 September 2020: Abstract syntax and operational semantics
There are PDF slides for 9/15/2020.
Retrospective: Introduction to the study of programming languages, induction and recursion, and Impcore.
Pedagogical studies show that reflection about what you are learning really helps the learning process, so we will start each module by asking you to briefly reflect on what you learned in the previous module.
Write one thing you learned in the previous module and one question you have about that material.
Your responses may be anonymously shared with the rest of the class.
Reflection: Exploring composition in programming languages
Composition, which is the ability to build many sensible things using just a few construction principles, is a critical to programming languages. An example at the syntactic level is the ability to build bigger programs out of smaller pieces. To get some practice with this idea, complete the following exercises:
In C++, write down three expressions and two statements.
Now compose one of the three expressions with the two statements to make another statement.
Now compose all three expressions to make another expression.
Programming-language semantics
“Semantics” means “meaning.”
What problem are we trying to solve?
Know what’s supposed to happen when you run the code
Ways of knowing:
- People learn from examples
- You can build intuition from words
(Book is full of examples and words) - To know exactly, unambiguously, you need more precision
You may recall the beginner exercise “make a peanut butter and jelly sandwich”
- You can watch and learn, but a computer can’t
- We must specify exactly what must be done.
Why bother with precise semantics?
- Prepare to program in languages you’ve never seen before
- “X-ray glasses”
- Compare languages by translating into semantics
- Python and JavaScript are much more similar than they look
- C++ and Java are much different than they look
- Prove properties of programs and programming languages
- Useful for security audits and program optimizations
- Understand what a correct language implementation must do
The programming languages you encounter after 105 will certainly look different from what we study this term. But most of them will actually be the same. Studying semantics helps you identify that.
The payoff: Your new skills will apply
Behavior decomposes
We want a computational notion of meaning.
What happens when we run (* y 3)?
We must know something about *, y, 3, and function application.
Knowledge is expressed inductively
- Atomic forms: Describe behavior directly (e.g., constants, variables)
- Compound forms: Behavior specified by composing behaviors of parts
Example of domain where compositionaliy doesn’t apply: English spelling and pronunciation
fishvsghoti
- Both composed from letters, but no rules of composition guide pronunciation
Check your understanding: Principle of composition
The following questions are designed to give you practice with composition by asking you to think about how C statements and expressions are composed to form more complex C statements and expressions.
C has a construct of the form ___?___:___. For the result to be syntactically well formed, what kinds of things can go in the blanks?
- statements only
- expressions only
- a mix
Is the result of filling in the blanks in the above C construct
- always a statement?
- always an expression?
- either a statement or an expression, depending on whether the second two blanks were filled with expresions or statements?
C also has an if construct of the form if (___) ___; else ___;.
For the result to be syntactically well formed, what kinds of things can go in the blanks?
- statements only
- expressions only
- a mix
Is the result of filling in the blanks in the C if construct
- always a statement?
- always an expression?
- either a statement or an expression, depending on whether the second two blanks were filled with expresions or statements?
ASTs
Question: What do we assign behavior to?
Answer: The Abstract Syntax Tree (AST) of the program.
An AST is a data structure that represents a program.
A parser converts program text into an AST.
Question: How can we represent all while loops?
while (i < n && a[i] < x) { i++ }
Answer:
- Tag code as a while loop
- Identify the condition, which can be any expression
- Identify the body, which can be any expression
As a data structure:
- WHILEX(exp1, exp2), where
- exp1 is the representation of (i < n && a[i] < x), and
- exp2 is the representation of i++
Check your understanding: AST Representations
Which of the following is the AST representation of the concrete Impcore syntax (if (> x 9) 1 0)?
WHILEX( APPLY (Name '>', Explist ( VAR 'x', LITERAL LITERAL 1, LITERAL 0))](IFX( APPLY (Name '>', Explist ( VAR 'x', LITERAL 9)), LITERAL 0, LITERAL 1))(IFX( APPLY (Name '>', Explist ( VAR 'x', LITERAL 7)), LITERAL 1, LITERAL 0))(IFX( APPLY (Name '>', Explist ( VAR 'y', LITERAL 9)), LITERAL 1, LITERAL 0))(IFX( APPLY (Name '>', Explist ( VAR 'x', LITERAL 9)), LITERAL 1, LITERAL 0))
Key question: names
Reflection: What’s in a name?
We’ve talked about how composition is really important in giving meaning to programs: you can understand a program fragment such as (+ e1 e2) by understanding each of its pieces (+, e1, and e2) and then putting them together.
Some parts of programs can’t be broken down further. An integer, for example, doesn’t have any smaller pieces that are still an integer. But we can understand an integer just by look at the bits that comprise it (aka, its representation).
What about names, such as a variable x? A name doesn’t have any smaller pieces, so we can’t understand it by understanding its pieces. And a name doesn’t contain in itself its meaning the way an integer does.
Explain how you think language implementors might give meaning to a name.
Hint: think about how dictionaries give meanings to words.
From ASTs to behaviors
Check your understanding: Operational semantics judgments
We find the meaning of variables by looking them up in an environment.
- True
- False
If an Impcore name
fstands for a function, which environment will it be in?- ξ (“ksee”)
- ϕ (“fee”)
- ρ (“roe”)
- If an Impcore name
xis defined in environment ξ (meaningxis in the domain of ξ), then it represents- a global variable
- a function
- a formal parameter
16 September 2020: Judgments, Rules, and Proofs
There are PDF slides for 9/17/2020.
Handout: Redacted Impcore rules
Handout: Overview of Induction
Reflection: Modeling computation in math
Suppose the notation e ⇓ 3 means that expression e evaluates to 3 and the notation n ∈ dom ρ means that variable n is in the environment ρ (and hence is defined in ρ).
- How would you say an expression evaluates to
7? - How would you say formally that an expression like
(+ n 1)evaluates successfully only ifnis defined? - How would you say what
(set x 0)does, and also(set n 0), and(set m 0), without having to repeat yourself for every variable you want to set to0? - What information would you need to know what
(all-fours? 344)evaluates to? - Why would you want to write these expressions in math, instead of just writing in natural language?
Rules and metatheory
Reflection: Operational semantics judgments
What do you think the rules are for evaluating a literal and for evaluating a variable? Fill in the question marks with your best guess!
⟨
LITERAL(v), ξ, ϕ, ρ⟩ ⇓ ⟨?, ?, ?, ?⟩⟨
VAR(x), ξ, ϕ, ρ⟩ ⇓ ⟨?, ?, ?, ?⟩In the second judgment, how can you tell which environment x belongs to?
Check your understanding: Semantics of variables
Consider the semantic rules for assignment to variables FormalAssign and GlobalAssign.
If x is in both the global environment ξ and the formal environment ρ, which version takes precedent?
- Global (ξ)
- Formal (ρ)
During the execution of the expression set(x, e), which environments may change? (Check all that apply)
- ξ
- ρ
- ϕ
Reflection: Mapping semantics to code
Consider again the semantic rules for assignment to variables FormalAssign and GlobalAssign.
How might these rules guide a language implementor?
Check your understanding: C implementation of environment operations
- In the implementation of variable lookup, what C operation corresponds to the semantic check that x ∈ dom ρ?
isvalbound(e->var, formals)isvalbound(e->var, globals)fetchval(e->var, formals)
- In the implementation of assignment, what part of the semantic rules corresponds to the C operation of
bindval(e->set.name, v, globals)?
- x∈ dom(ρ)
- ρ′{x ↦ v}
- x∈ domξ
- ξ′{x ↦ v}
Note that the implementation doesn’t precisely follow the semantics. Instead of returning a new environment as directed by the semantics, the implementation instead updates the old environment in place using a side-effecting operation. This choice is more efficient than copying the old environment. It’s a metatheorem of Impcore that this optimization is sound. It’s a metatheorem that will no longer hold when we shift to Scheme and start copying environments to form closures.
Reflection: Using semantics to understand how programs are evaluated
Consider the following code:
(define and (p q)
(if p q 0))
(define digit? (n)
(and (<= 0 n) (< n 10)))Suppose we evaluate (digit? 7)
- In the body of
digit?, what expressions are evaluated in what order?
The body of the
digit?function matches the template(f e1 e2)where f, e1, and e2 are meta-variables that stand for different program fragments. In matching the template to the body ofdigit?,- What is f?
- What is e1?
- What is e2?
Good and bad judgments
Reflection: Good and bad judgments
Just because something is written in math notation doesn’t make it true!
Which of the following judgements correctly describe what happens at runtime? Explain your answers. Pay special attention to the lack of primes on the concluding environments.
⟨
(+ 2 2), ξ, ϕ, ρ⟩ ⇓ ⟨4, ξ, ϕ, ρ⟩⟨
(+ 2 2), ξ, ϕ, ρ⟩ ⇓ ⟨99, ξ, ϕ, ρ⟩⟨
(+ 2 2), ξ, ϕ, ρ⟩ ⇓ ⟨4, ∅, ϕ, ρ⟩⟨
(while 1 0), ξ, ϕ, ρ⟩ ⇓ ⟨77, ξ, ϕ, ρ⟩⟨
(begin (set n (+ n 1)) 17), ξ, ϕ, ρ⟩
⇓ ⟨17, ξ, ϕ, ρ⟩
Proofs: Putting rules together
Every terminating computation is described by a data structure—we’re going to turn computation into a data structure: a tree. Proofs about computations are hard (see: COMP 170), but proofs about trees are lots easier (see: COMP 61).
How do we know it’s right?
From rules to proofs
<– The ``Tony Hawk’’ algorithm –>
Building a derivation
Building derivations
Check your understanding: Derivation trees
- In constructing the derivation tree for the program
(digit? 7), what is the rule at the bottom of the tree?
- ApplyUser
- Var
- Literal
- What environment will be used to find the meaning of the name
digit??
- ξ
- ϕ
- ρ
- What rule will be used to find the meaning of the sub-expression
7?
- ApplyUser
- Var
- Literal
21 September 2020: Derivations and metatheory
There are PDF slides for 9/22/2020.
All your operational-semantics questions are answered.
Reflection: Metatheory vs theory
Metatheory allows us to prove properties about all derivations, which means it allows us to prove properties about all programs in a language.
The derivation that demonstrates that (digit? 7) evaluates to true is a proof about that particular program, so it theory but not metatheory. A metatheoretic property about Java is that in a well-typed program, every variable mentioned in the program has previously been defined.
Classify the following properties as theory or metatheory:
The evaluation of any Impcore program will never access undefined memory.
- theory
- metatheory
The evaluation of
(and (<= 0 n) (< n 10))will access the value associated with the variablen.- theory
- metatheory
For any Impcore program
p, every variable mentioned inpwill be in the domain of either ξ, ϕ, or ρ.- theory
- metatheory
Note: a theoretic or metatheoretic property can be either true or false. The distinction is whether the property would apply only to specific programs or to all programs were it to be true. The proof methods used to prove theoretic and metatheoretic properties differ because a theory proof applies only to a specific program while a metatheoretic proof applies to all programs in a language.
Proofs about all derivations: metatheory
Reflection: Writing metatheoretic properties
- Using the judgment form for Impcore evaluation that we are already familiar with, ⟨e, ξ, ϕ, ρ⟩ ⇓ ⟨v, ξ′, ϕ′, ρ′⟩, how would you formally write “In Impcore, evaluation doesn’t change the set of defined global variables?”?
- Using the judgment form for Impcore evaluation that we are already familiar with, ⟨e, ξ, ϕ, ρ⟩ ⇓ ⟨v, ξ′, ϕ′, ρ′⟩, how would you formally write “In Impcore, evaluation doesn’t change the values of any global variables”?
Cases to try:
- Literal
- GlobalVar
- SetGlobal
- IfTrue
- ApplyUser2
For your homework, “Simplified Impcore” leaves out While and Begin rules.
Check your understanding: Proving metatheoretic properties
The following questions all relate to the metatheoretic proof that evaluation in Impcore does not change the set of defined global variables, ie, for any Impcore expression e, if ⟨e, ξ, ϕ, ρ⟩ ⇓ ⟨v, ξ′, ϕ′, ρ′⟩, then dom(ξ) = dom(ξ′). We prove this property by induction on the derivation of ⟨e, ξ, ϕ, ρ⟩ ⇓ ⟨v, ξ′, ϕ′, ρ′⟩.
The proof proceeds by case analysis on the last rule used in the derivation ⟨e, ξ, ϕ, ρ⟩ ⇓ ⟨v, ξ′, ϕ′, ρ′⟩.
- True
- False
One of the rules that must be considered is the IfFalse rule
- True
- False
The case for GlobalVar is an inductive case.
- True
- False
The case for GlobalAssign is an inductive case.
- True
- False
Summary and Next Steps
Theory: Operational semantics
- A “high-level assembly language”
- Justify algebraic laws
- Guide to implementation
(Will return to formal rules about code in about a month)
Practice: For the next month, programming!
Return to algebraic laws! Lean on them!
23 September 2020: Scheme I: Recursive Programming with Lists and S-Expressions
There are PDF slides for 9/24/2020.
Retrospective: Operational Semantics
Write one thing you learned about operational semantics and one question you still have. Your answers may be anonymously shared with your classmates.
Reflection: From inference rules to recursive functions
In the previous module, you encountered a whole bunch of inference rules. How do you think those inference rules related to functions? When might they be recursive functions?
For a new language, five powerful questions
As a lens for understanding, you can ask these questions about any language:
What are the values? What do expressions/terms evaluate to?
What environments are there? That is, what can names stand for?
What is the abstract syntax? What are the syntactic categories, and what are the forms in each category?
How are terms evaluated? What are the judgments? What are the evaluation rules?
What’s in the initial basis? Primitives and otherwise, what is built in?
(Initial basis for μScheme on page 99)
Introduction to Scheme
Why Scheme?
Vehicle to study recursion and composition, two powerful programming techniques:
Recursive functions in depth
Two recursive data structures: the list and the S-expression
More powerful ways of putting functions together (compositionality again, and it leads to reuse)
Today: programming with lists and S-expressions using algebraic laws
Two new kinds of data:
The function closure: the key to “first-class” functions
Pointer to automatically managed cons cell (mother of civilization)
Scheme Values
Most values are S-expressions.
An fully general S-expression is one of
a symbol
'Halligan'tuftsa literal integer
077a literal Boolean
#t#f(consv1 v2), where v1 and v2 are S-expressions
It is very common to work with a list of S-expressions, which is either
- the empty list
'() (consv vs), where v is an S-expression and vs is a list of S-expressions
We say “an S-expression followed by a list of S-expressions”
Lists: A subset of S-Expressions.
These are your linked lists from COMP 11 or COMP 15.
Can be defined via a recursion equation or by inference rules:
Check your understanding: S-Expressions
- Every Scheme list is an S-expression.
- True
- False
- Every Scheme S-expression is a List(A) for some A.
- True
- False
- Select each of the following S-expressions that are also List(A) where A is the set of symbols.
(cons 'Tufts 'Jumbos)(cons 'Tufts '())(cons '2020 '())
Reflection: Manipulating values
Values are only useful to the extent that they can be manipulated. What operations do you think would be useful to have on a
conscell?Recall how we defined numbers via different inductive definitions in Impcore. Using similar thinking, what cases will we need to handle for lists?
Understanding values through their operations
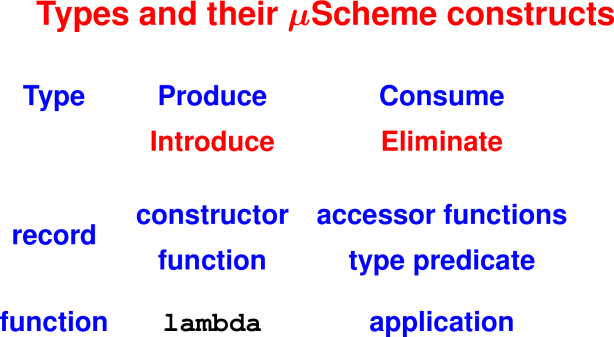
Constructors:
- Form values
- List constructors:
'()andcons - Any list is therefore constructed with
'()or withconsapplied to a value and a smaller list.
Observers:
- These ask, “how were you formed, and from what parts?”
- They are
null?,pair?,car, andcdr(carandcdralso known as “first” and “rest”, “head” and “tail”, and many other names)
Laws of lists:
(null? '()) == #t
(null? (cons v vs)) == #f
(car (cons v vs)) == v
(cdr (cons v vs)) == vsCheck your understanding: Deconstructing lists
A list is formed with either '() or cons.
- What operation distinguishes between these two types of list?
carcdrnull?
- Given this structure, how many cases will a function that consumes a list typically have?
- 0
- 1
- 2
- 3
Why are lists useful?
Sequences a frequently used abstraction
Can easily approximate a set
Can implement finite maps with association lists (aka dictionaries)
You don’t have to manage memory
These “cheap and cheerful” representations are less efficient than balanced search trees, but are very easy to implement and work with—see the book.
The only thing new here is automatic memory management. Everything else you could do in C. (You can have automatic memory management in C as well.)
Programming with lists: The member? function
;; forms of data
;; '()
;; (cons n ns) where n is a number and
ns is a list of numbers
;; example inputs
(val x1 '())
(val x2 '(1 2 3 4))
(val x3 '(8))
(val x4 '(10 10))
;; Write check assert cases now
;; Algebraic Laws
;; (member? n '()) = #f
;; (member? n (cons n ns)) = #t
;; (member? n (cons n' ns)) = (member? n ns),
where n' != n
;; The code!
;; return true if and only if
;; list of numbers ms contains
;; number m
(define member? (m ms)
(if (null? ms)
(if (= m (car ms))
(member? m (cdr ms)))))
(check-assert (not (member? 8 '())))
(check-assert (not (member? 8 '(1 2 3))))
(check-assert (member? 8 '(8)))
(check-assert (member? 8 '(10 7 8 12)))
Coding Interlude: member?
Consider the member? code from the previous video. Run the code on the sample data.
Add a
check-assertcase where the element is in the list.Add a
check-assertcase where the element is not in the list.
- Live coding: do two distinct elements sum to 16?
Programming with lists: The sum-16? function
Do two distinct list elements sum to 16?
;; forms of data
;; '()
;; (cons n ns) where n is a number and
ns is a list of numbers
;; example inputs
(val x5 '(6 10))
(val x6 '(3 6 12 7 8 9 10))
;; Write check assert cases now
;; Algebraic Laws
;; (sum-16? '()) = #f
;; (sum-16? (cons n ns)) =
;; (sum-16? ns) OR
;; n and an element in ns sum to 16
;; i.e., (member? (- 16 n) ns))
;; The code!
;; returns #t if and only if ms contains
;; two distinct elements that sum to 16,
;; where ms is a list of numbers
(define sum-16? (ms)
(if (null? ms)
(|| (sum-16? (cdr ms))
(member? (- 16 (car ms)) (cdr ms)))))
(check-assert (not (sum-16? x1)))
(check-assert (not (sum-16? x2)))
(check-assert (not (sum-16? x3)))
(check-assert (not (sum-16? x4)))
(check-assert (sum-16? x5)))
(check-assert (sum-16? x6)))
Coding Interlude: sum-16?
Consider the sum-16? code from the previous video. Run the code on the sample data.
Modify the algebraic laws and the code to check if the product of two elements in the list equals 16. Note that * and / are the multiplication and division operations in μScheme.
Reflection: Quote syntax
Nobody wants to write a constant list of numbers as (cons 0 (cons 1 (cons 2 (cons 3 (cons 4 (cons 5 (cons 6 (cons 7 (cons 8 (cons 9 '())))))))).
What notation would you suggest instead?
Check your understanding: Quoted literals
Write each ordinary S-expression using quote syntax:
(cons 1 '())= BLANK1(cons 1 (cons 2 '()))= BLANK2(cons (cons 1 '()) '())= BLANK3(cons (cons 'a (cons 'b '())) (cons 'c '()))= BLANK4
Reflection: New syntactic forms
To program with lists and S-expressions, we absolutely have to have functions like null?, cons, car, and cdr. And the quote syntax is certainly useful. To make it even easier to program with S-expressions, what other new syntax might be useful?
μScheme’s new syntax
28 September 2020: First-class and higher-order functions
There are PDF slides for 9/29/2020.
Big picture:
- Think of S-expressions and lists, not pointers
- Write less code and reuse more code
Retrospective: Scheme I: Recursive programming with lists
Write one thing you learned in the previous module. Your answers may be anonymously shared with your classmates.
es
Reflection: Where is there shared structure?
Functions are values
Reflection: Shared structure
Implementing any-two?
Check your understanding: The exists? function
The call (exists? even? '()) returns
#t#f
The call (exists? odd? '(0 2 4 7 8)) returns
#t#f
How many of the items in the list does the call to (exists? odd? '(0 2 4 7 8)) examine?
045
Introduction to lambda
(define any-two? (q? xs)
;; tell if any two elements y and z
;; in order satisfy (q? y z)
(if (null? xs)
(|| (any-two? q? (cdr xs))
(exists? (lambda (z) (q? (car xs) z))
(cdr xs)))))Check your understanding: Lambda
Consider the following code when answering the questions below:
(define combine (p1? p2?)
(lambda (x) (if (p1? x) (p2? x) #f)))
(define divvy (p1? p2?)
(lambda (x) (if (p1? x) #t (p2? x))))
(val c-p-e (combine prime? even?))
(val d-p-o (divvy prime? odd?))The expression
(c-p-e 9)equals#t#f
The expression
(c-p-e 8)equals#t#f
The expression
(c-p-e 7)equals#t#f
The expression
(d-p-o 9)equals#t#f
The expression
(d-p-o 8)equals#t#f
The expression
(d-p-o 7)equals#t#f
Escaping functions
μScheme’s semantics: Overview and let
Reflection: Scheme vs Impcore
We’ve now studied two different languages: Impcore and μScheme.
Name two things you can do in μScheme that you can’t do in Impcore.
Speculate on how the semantics of μScheme might differ from that of Impcore to account for those features.
It’s not precisely true that rho never changes.
New variables are added when they come into scope.
Old variables are deleted when they go out of scope.
But the location associated with a variable never changes.
Strange syntax, but simple semantics!
Key idea: don’t worry about memory
Check your understanding: meta-variables
Consider the semantic rule for let.
Match the meta-variables with their meanings.
Meta-variables:
- e
- ρ
- σ
- v
- ℓ
- x
Meanings:
- The names that are being given values.
- The expressions that specify the values to associate with each variable.
- The values the expressions evaluate to.
- The locations where values will be stored.
- The environment that associates variable names with locations.
- The store that maps locations to values.
Another way to write this one:
- The names that are being given values.
- The expressions that specify the values to associate with each variable.
- The values the expressions evaluate to.
- The locations where values will be stored.
- The environment that associates variable names with locations.
- The store that maps locations to values.
Check your understanding: The semantics of let
Consider the semantic rule for let.
Expression e1 is evaluated after expression e2.
- True
- False
The memory cells allocated for x1 and x2 must be distinct, meaning they cannot alias.
- True
- False
In evaluating the body of the let e, any side effects that occured during the evaluation of e1 and e2 will be visible and variables x1 and x2 will be in scope.
- True
- False
Semantics of lambda
Key idea: ``every name I can see—remember where it is stored.’’
Check your understanding: Semantics of lambda
Consider the semantic rule for lambda.
Side effects (changes to the global store) triggered by the evaluation of the body of the lambda (ie, e) will take place during the evaluation of the lambda.
- True
- False
The environment captured in the closure is the same as the environment in force at the point where the lambda appears in the source program
- True
- False
Semantics of function application
Questions about ApplyClosure:
What if we used σ instead of σ0 in evaluation of e1?
What if we used σ instead of σ0 in evaluation of arguments?
What if we used ρc instead of ρ in evaluation of arguments?
What if we did not require ℓ1, ℓ2 ∉ dom(σ)?
What is the relationship between ρ and σ?
Check your understanding: Semantics of application
Consider the semantic rule for ApplyClosure2.
Which expression evaluates to a closure?
- e
- e1
- e2
- ec
Which expression represents the first argument to the function?
- e
- e1
- e2
- ec
Which expression represents the body of the function being applied?
- e
- e1
- e2
- ec
In what order are the expressions mentioned in the rule evaluated?
- e1, e2, ec, e
- ec, e1, e2, e
- e, e1, e2, ec
- ec, e2, e1, e
Which environment is in force at the point where the body of the function is evaluated?
- ρ
- ρc
- ρc{x1 ↦ ℓ1, x2 ↦ ℓ2}
Immutable data: its costs and benefits (not covered in class)
Key idea of functional programming: constructed data. Instead of mutating, construct a new one. Supports composition, backtracking, parallelism, shared state.
Already doing it: immutable data (append)
- Always safe to share data (I can’t mess up things for you)
- Perfect for parallel/distributed (think Erlang)
- Perfect for web (JSON, XML)
Cost model
The major cost center is cons because it corresponds to allocation.
How many cons cells are allocated?
Let’s rigorously explore the cost of append.
Structural Induction Principle for List(A)
Suppose I can prove two things:
IH (’())
Whenever a in A and also IH(as), then IH (cons a as)
then I can conclude
Forall as in List(A), IH(as)
Claim: Cost (append xs ys) = (length xs)
Proof: By induction on the structure of xs.
Base case: xs = ’()
I am not allowed to make any assumptions.
(append '() ys) = { because xs is null } ysNothing has been allocated, cost is zero
(length xs)is also zero.Therefore, cost =
(length xs).
Inductive case: xs = (cons z zs)
I am allowed to assume the inductive hypothesis for
zs.Therefore, I may assume the number of cons cells allocated by
(append zs ys)equals(length zs)Now, the code:
(append (cons z zs) ys) = { because first argument is not null } = { because (car xs) = z } = { because (cdr xs) = zs } (cons z (append zs ys))The number of cons cells allocated is 1 + the number of cells allocated by
(append zs ys).cost of (append xs ys) = { reading the code } 1 + cost of (append zs ys) = { induction hypothesis } 1 + (length zs) = { algebraic law for length } (length (cons z zs)) = { definition of xs } (length xs)
Conclusion: Cost of append is linear in length of first argument.
More functional programming (not covered in class)
List-design shortcuts
Three forms of “followed by”
Given: Element .. list of values =
(cons x xs)Define: List of values .. list of values =
(append xs ys)Ignore: List of values .. element =
(snoc xs y)
Or(append xs (list1 y))
Two lists? Four cases!
Using informal math notation with .. for “followed by” and e for the empty sequence, we have these laws:
xs .. e = xs
e .. ys = ys
(z .. zs) .. ys = z .. (zs .. ys)
xs .. (y .. ys) = (xs .. y) .. ysThe underlying operations are append, cons, and snoc. Which ..’s are which?
But we have no
snocIf we cross out the
snoclaw, we are left with three cases… but case analysis on the first argument is complete.So cross out the law
xs .. e == xs.Which rules look useful for writing append?
Costs of list reversal
Algebraic laws for list reversal:
reverse '() = '()
reverse (x .. xs) = reverse xs .. reverse '(x) = reverse xs .. '(x)And the code?
The list1 function maps an atom x to the singleton list containing x.
How many cons cells are allocated? Let’s let n = |xs|.
- Q: How many calls to
reverse? A:n - Q: How many calls to
append? A:n - Q: How long a list is passed to
reverse? A:n-1,n-2, … ,0 - Q: How long a list is passed as first argument to
append? A:n-1,n-2, … ,0 - Q: How many
conscells are allocated by call tolist1? A: one per call toreverse. - Conclusion: O(n2) cons cells allocated. (We could prove it by induction.)
The method of accumulating parameters
Write laws for
(revapp xs ys) = (append (reverse xs) ys)Who could write the code?
The cost of this version is linear in the length of the list being reversed.
Parameter ys is the accumulating parameter.
(A powerful, general technique.)
30 September 2020: Higher-order functions
There are PDF slides for 10/1/2020.
Reflection: List functions
Consider the function, with the algebraic laws:
This algorithm searches for an element in a list.
List other algorithms you are familiar with that operate over a list (or linked list, or an array) and explain briefly what they do.
List search: exists?
Algorithm encapsulated: linear search
Example: Is there a number in the list?
Algebraic laws:
(exists? p? '()) == ???
(exixts? p? (cons x xs)) == ???
(exists? p? '()) == #f
(exists? p? (cons x xs)) == #t,
if (p? x)
(exixts? p? (cons x xs)) == exists? p? xs,
otherwiseCoding Interlude: exists?
Define a list ys and two predicates p1? and p2? such that exists? p1? ys evaluates to #t and exists? p2? ys evalutes to #f. Run the code to confirm your answers are correct.
An alternative formulation of the algebraic laws for the exists? function is:
;; (exists? p? '() = #f
;; (exists? p? (cons x xs)) = (|| (p? x)
;; (exists? p? xs))Modify the definition of exists? following this algebraic formulation instead, and re-run your examples.
List selection: filter
Algorithm encapsulted: Filter list according to a predicate
Example: Keep positive numbers in a list.
Coding Interlude: filter
Use lambda to define a predicate that returns true iff the argument is a number larger than 9.
Define a list ys that contans a mix of one- and two-digit numbers.
Use your lambda function and the filter function defined in the video to produce a new list zs that contains only the elements in ys with at least two-digits.
Run your code.
How would you modify the code to produce a list with only one-digit numbers?
Reflection: Lifting functions to lists: map
Consider the map function. The algorithm it encapsulates is to transform every element according to an argument function. If sq is the function that squares its argument, then map sq '(1,2,3) will produce the list '(1,4,9).
Please complete the algebraic laws for the map function:
(map f '()) == ???
(map f (cons n ns)) == ???Algorithm encapsulated: Transform every element according to argument function
Example: Square every element of a list.
Algebraic laws:
(map f '()) == '()
(map f (cons n ns)) == (cons (f y) (map f ys))The universal list function: foldr
Algorithm encapsulated: Aggregate all elements in a list.
Example: What is the sum of the numbers in a list?
foldr takes two arguments:
zero: What to do with the empty list.plus: How to combine next element with running results.
Example: foldr plus zero '(a b)
cons a (cons b '())
| | |
v v v
plus a (plus b zero)Check your understanding:
What does the following code evaluate to?
-> (define foldr (plus zero xs)
(if (null? xs)
zero
(plus (car xs) (foldr plus zero (cdr xs)))))
-> (define combine (x a) (+ 1 a))
-> (foldr combine 0 '(2 3 4 1))010244
Reflection: Language design: Why the redundancy?
We’ve just seen that functions like exists?, map, and filter can all be easily written in terms of the foldr function. The foldr function, in turn, can easily be written in terms of basic recursion. Other languages have similar redundancy involving loops: for, while, etc.
It takes extra effort for library designers to code more functions or for language designers to support more features.
What do you think makes it worth their effort to support this range of functions and looping constructs?
Currying
Deriving one-argument functions from two-argument functions
Check your understanding:
What does the following code evaluate to?
-> (map ((curry +) 3) '(1 2 3 4 5))1518'(4 5 6 7 8)'(1 2 3 3 4 5)'(3 4 5 6 7 8)4
-> (exists? ((curry =) 3) '(1 2 3 4 5))'()#t#f0
-> (filter ((curry >) 3) '(1 2 3 4 5))
; tricky
'(1 2)'(1 2 3)- ’()
'(3 4 5)'(4 5)
Composing functions
Coding Interlude: compose
The predicate null? returns #t iff the argument list is empty, while the function not inverts a boolean. Use the compose function (o) to write a predicate that tests whether a list is non-empty.
Run your code on both empty and non-empty lists.
Proofs about functions
5 Oct 2020: Costs, tail calls, and continuations
There are PDF slides for 10/6/2020.
Retrospective: Higher-order functions retrospective
Write one thing you learned about higher-order and anonymous functions. Your answers may be anonymously shared with your classmates.
Reflection: Expected performance
Consider the following algebraic laws for list reversal:
reverse '() = '()
reverse (x .. xs) = reverse xs .. reverse '(x)
= reverse xs .. '(x)where .. denotes the append operation on lists.
Now consder the corresponding code:
(define reverse (xs)
(if (null? xs)
'()
(append (reverse (cdr xs))
(list1 (car xs)))))where list1 is a function that makes a one-element list from its argument.
Answer these questions:
- For a list reversal function to be considered to have good performance, what should its running time be in terms of the length of its argument?
- What is the running time of the
reversefunction above?
Where have we been, where are we going: functions
Today: costs and control flow
Costs of list reversal
Consider the call reverse xs and let n = |xs|.
How many stack frames are allocated for reverse and append?
How many cons cells are allocated?
- Q: How many calls to
reverse? A:n - Q: How many calls to
append?
A:n - Q: How long is list passed to
reverse?
A:n-1,n-2, … ,0 - Q: How long is list passed as 1st arg to
append?
A:n-1,n-2, … ,0 - Q: How many
conscells are allocated by call tolist1? A: one per call toreverse. - Conclusions: (We could prove by induction.)
- O(n) stack frames are allocated.
- O(n2) cons cells allocated.
- Function is quadratic.
Alarm bells should be ringing: Reversing a list should be linear!
We’ll get to a linear verson of list reversal via tail calls and the method of accumulating parameters.
Tail calls
Check your understanding: Tail Position
Consider the following code
-> (define foldr (plus zero xs)
(if (null? xs)
zero
(plus (car xs) (foldr plus zero (cdr xs)))))Now answer the following questions.
The occurrence of expression zero in the true-branch of the if expression is in tail position.
- True
- False
The occurrence of expression plus in the false-branch of the if expression is in tail position.
- True
- False
The occurrence of expression foldr in the false-branch of the if expression is in tail position.
- True
- False
Tail calls and the method of accumulating parameters
We’ll seee that the cost of this version is linear in the length of the list being reversed.
Parameter ys is the accumulating parameter.
Example: revapp '(1 2) '()
Call stack: (each line replaces previous one)
revapp '(1 2) '() -->
revapp '(2) '(1) -->
revapp '() '(2 1)Consider the call revapp xs '() and let n = |xs|.
How many stack frames are allocated?
How many cons cells are allocated?
- Q: How many calls to
revapp? A:n - Q: How many of them are tail calls? A:
n - Q: How many stack frames are allocated for
revapp? A:1 - Q: How much work is done per call to
revapp? A: constant. - Conclusions: (We could prove by induction.)
- O(1) stack frames for
revappare allocated. - O(n) cons cells allocated.
- Function is linear in length of list being reversed.
- O(1) stack frames for
Check your understanding: Accumulating Parameters
An accumulating parameter to a recursive function f accumulates the answer so that a recursive call to f can be in tail position.
- True
- False
The stack frame of a function call that is not in tail position cannot be shared with subsequent calls because its values may still be needed.
- True
- False
Tail-call optimizations and the use of accumulating parameters can only result in constant-time improvements to the complexity of a function.
- True
- False
Continuations
Reflection: Another construct that transfers control
Are tail calls familiar? What other programming construct
Transfers control to another point in the code?
Uses no stack space?
Check your understanding: Continuation Introduction
A continuation is different from a normal function because it never returns to the context from which it was invoked.
- True
- False
Continuations cannot take arguments.
- True
- False
Continuations are used in GUI frameworks and to mimic exceptions.
- True
- False
Motivating Example: Using continuations to signal exceptions
Reflection: Handling unusual circumstances
Consider the following algebraic laws for a witness function:
(witness p? xs) == x, where (member x xs),
provided (exists? p? xs)Now answer this questions:
- What should the function do if there exists no such
x?
Question: How much stack space is used by the call?
Answer: Constant
Coding Interlude: witness-cps
Consider the following code:
(define witness-cps (p? xs succ fail)
(if (null? xs)
(fail)
(let ([z (car xs)])
(if (p? z)
(succ z)
(witness-cps p? (cdr xs) succ fail)))))
(val 2020f '((Fisher 105)(Monroe 40)(Chow 116)))
(define instructor-info (instructor classes)
(let (
[s (lambda (info) ; success continuation
(list3 instructor 'teaches (cadr info)))]
[f (lambda () ; failure continuation
(list2 instructor 'is-not-on-the-list))])
(witness-cps (o ((curry =) instructor) car)
classes s f)))
(instructor-info 'Fisher 2020f)
(instructor-info 'Chow 2020f)
(instructor-info 'Votipka 2020f)Modify the code to add another professor and course number, and add a test case for that professor.
Run your code.
Modify the code to return 'is-not-teaching-this-semester if the instructor’s name is not on the list.
Run your code to confirm it returns your new response when given a name not on the list.
Explain how would you modify the code to search for a course number instead of an instructor name.
7 Oct 2020: Continuations for backtracking
There are PDF slides for 10/8/2020.
Reflection: Solving Boolean formulas
On your homework, you will use continuations to organize a search to find satisfying assignments for Boolean formulas.
A formula has one of these forms:
given the following record declarations:
For each formula, find a satisfying assignment or explain why none exists.
(val f1 (make-and (list4 'x 'y 'z (make-not 'x))))
; x /\ y /\ z /\ !x
(val f2 (make-not (make-or (list2 'x 'y))))
; !(x \/ y)
(val f3 (make-or (list2 'x 'y)))
; x \/ y
(val f4 (make-not (make-and (list3 'x 'y 'z))))
; !(x /\ y /\ z)Searching via continuations: An example
Continuations for Search
the name of the literal in the box.
Solving a Literal
start carries a partial truth assignment to variables current
Box describes how to extend current to make a variable, say x, true.
Case 1: current(x) = #t
Call success continuation with current
Pass fail as resume continuation (argument to success)
Case 2: current(x) = #f
Call fail continuation
Case 3: x not in current
Call success continuation with current{x -> #t}
Pass fail as resume continuation
Check your understanding: Solving a Negated Literal
Consider the schema we’ve been using to find satisfying assignments for Boolean formulas. In the previous video, we walked through how to instantiate the schema for a positive literal. The following questions ask you to do the same thing for a negated literal, which is a term of the form not x where x is a literal.
The start continuation is called with argument current, the partial truth assignment constructed so far. The box needs to describe how to extend current to make the negated variable not x true.
If current(x) = #t, what should the box do?
- Call
successcontinuation withcurrentas argument. - Call
failcontinuation - Call
successcontinuation withcurrentextended with{x->#t} - Call
successcontinuation withcurrentextended with{x->#f}
If current(x) = #f, what should the box do?
- Call
successcontinuation withcurrentas argument. - Call
failcontinuation - Call
successcontinuation withcurrentextended with{x->#t} - Call
successcontinuation withcurrentextended with{x->#f}
If x is not in current, what should the box do?
- Call
successcontinuation withcurrentas argument. - Call
failcontinuation - Call
successcontinuation withcurrentextended with{x->#t} - Call
successcontinuation withcurrentextended with{x->#f}
The success continuation takes two arguments: current (the partial solution found so far) and resume (the continuation that takes over if current is found to be inconsistent with some new part of the formula. When calling the success continuation, what should we pass as the resume continuation?
(lambda (x) x)fail(lambda (x) (not x))start
Please explain your answer.
Solving A and B
Solver enters A
If A is solved, newly allocated success continuation starts B
If B succeeds, we’re done! Use
successcontinuation from context.If B fails, use
resumecontinuation A passed to B asfail.If A fails, the whole thing fails. Use
failcontinuation from context.
Solving A or B
Solver enters A
If A is solved, we’re good! But what if context doesn’t like solution? It can resume A using the resume continuation passed out as
fail.If A can’t be solved, don’t give up! Try a newly allocated failure continuation to start B.
If ever B is started, we’ve given up on A entirely. So B’s success and failure continuations are exactly the ones in the context.
If B succeeds, but the context doesn’t like the answer, the context can resume B.
If B fails, abject failure all around; call the original
failcontinuation.
Lisp and Scheme Retrospective
Common Lisp, Scheme
Advantages:
- High-level data structures
- Cheap, easy recursion
- Automatic memory management (garbage collection!)
- Programs as data!
- Hygenic macros for extending the language
- Big environments, tiny interpreters, everything between
- Sophisticated Interactive Development Environments
- Used in AI applications; ITA; Paul Graham’s company Viaweb
Down sides:
- Hard to talk about data
- Hard to detect errors at compile time
Bottom line: it’s all about lambda
- Major win
- Real implementation cost (heap allocation)
Next time: think about good and bad points
Bonus content: Scheme as it really is
- Macros!
- Cond expressions (solve nesting problem)
- Mutation
- …
Macros!
Conditional expressions
Mutation
12 Oct 2020: Introduction to ML
There are PDF slides for 10/13/2020.
Retrospective: Continuations
Write one thing you learned about continuations. Your answers may be anonymously shared with your classmates.
Reflection: μScheme evaluation
Evaluating an idea or an artifact is an advanced cognitive task:
- Remember
- Understand
- Apply
- Analyze
- Evaluate
- Create
Given what you have learned so far in this course, you are in a good position to start to evaluate μScheme.
Please enter at least two strengths of μScheme:
Please enter at least two weaknesses of μScheme.
Your answers may be anonymously shared with your classmates.
The language that we will study next, ML, addresses some of the weaknesses of μScheme.
Introduction to ML
Meta: Apply your new knowledge in Standard ML:
- You’ve already learned (most of) the ideas
- There will be a lot of new detail
- Not your typical introduction to a new language
- Not definition before use, as in a manual
- Not tutorial, as in Ullman
- Instead, the most important ideas that are most connected to your work up to now
ML Overview
- Designed for manipulating programs, logic, and symbolic data
- Good language for implementing language features
- Good language for studying type systems
- Theme: Precise ways to describe data
Three new ideas
ML = uScheme + pattern matching + static types + exceptions
- Pattern matching is big and important. You will like it. It’s “coding with algebraic laws”
- Static types get two to three weeks in their own right.
- Exceptions are easy
Pattern matching makes code look more like algebraic laws: one pattern for each case
Static types tell us at compile time what the cases are.
Exceptions solve the problem “I can’t return anything sensible!”
And lots of new concrete syntax!
Example: The length function.
Algebraic laws:
length [] = 0 length (x::xs) = 1 + length xsThe code:
fun length [] = 0 | length (x::xs) = 1 + length xs val res = length [1,2,3]Things to notice:
No brackets! (I hate the damn parentheses)
Function application by juxtaposition
Function application has higher precedence than any infix operator
Compiler checks all the cases (try in the interpreter)
Coding Interlude: length
Use the length function
fun length [] = 0
| length (x::xs) = 1 + length xsto calculate the length of the list [1,2,3,4].
Now write the sum function in ML that calculates the sum of the same list.
μScheme to ML Rosetta stone
uScheme SML
(cons x xs) x :: xs
'() []
'() nil
(lambda (x) e) fn x => e
(lambda (x y z) e) fn (x, y, z) => e
|| && andalso orelse
(let* ([x e1]) e2) let val x = e1 in e2 end
(let* ([x1 e1] let val x1 = e1
[x2 e2] val x2 = e2
[x3 e3]) e) val x3 = e3
in e
endCheck your understanding: ML Syntax
Match the μScheme syntax with its ML equivalent.
μScheme:
&&
(lambda (x y z) e)
'()
||
(lambda (x) e)
(let* ([x e1]) e2)
(cons x xs)
'()
(let* ([x1 e1]
[x2 e2]
[x3 e3]) e)
ML
fn (x, y, z) => e
nil
fn x => e
x :: xs
andalso
[]
false
let val x = e1 in e2 end
true
let val x1 = e1
val x2 = e2
val x3 = e3
in e
end
orelse
ML forms of data
Live coding:
(* ML's comment form *)
bool (* true, false *)
string (* "Tufts" *)
char (* #"A" *)
int (* including negative integers, eg ~12 *)
list of int [1,2,3]
list of bool [true, false]
ill-typed list [1, true]
pair (1, "Halligan")
triple (105, "Scheme", true)Check your understanding: Simple ML Types
Which of the following is not syntactically correct ML code?
[1,2,3,5](* This is a comment *) [true, false, true](true, "hello")~12#"K"- None of the above
ML Functions
(* Can't use ? in the names of functions in ML *)
fun even x = (x mod 2 = 0)
fun map f [] = []
| map f (y :: ys) = f y :: map f ys
(* Anonymous functions are more verbose in ML *)
val res1 = map (fn (x) => (x + 1)) [1,2,3]
(* ML also has a case statement;
It's not as elegant as clausal definitions. *)
(* orelse shortcircuits *)
fun exists p xs =
case xs
of [] => false
| y :: ys => p y orelse exists p ys
val res2 = exists even [1,2,3,4](* Higher order functions exist in ML too *)
(* Notation (op +) converts infix to prefix *)
fun sum xs = foldr (op +) 0 [1,2,3,4]
Check your understanding: ML Functions
Which of the following functions correctly implements the filter function, defined by the following algebraic laws? (Note, all of the functions are syntatically correct.)
filter p [] = []
filter p (y :: ys) =
if p y then y :: filter p ys
else filter p ysfun filter p xs =
case xs
of [] => []
| y :: ys =>
if p y then y :: filter p ys
else filter p ys fun filter p [] = []
| filter p (y :: ys) =
if p y then y :: filter p ys
else filter p ysfun filter p xs =
foldr (fn(x,a) =>
if p x then (x::a) else a)
[] xsAll of the above.
New Forms of Data
Example: Binary Tree of Integers
(* LEAF and NODE are called data type constructors *)
datatype itree = LEAF
| NODE of itree * int * itree
(* Data type constructors build data structures*)
(* and can be used in pattern matching *)
fun insert n LEAF =
NODE (LEAF, n, LEAF)
| insert n (NODE (left, m, right)) =
if n < m then
NODE (insert n left, m, right)
else if n > m then
NODE (left, m, insert n right)
else
NODE (left, m, right)
(* insert is curried;
we might also want an uncurried version of insert *)
fun insert' (n, tree) = insert n tree
(* @ is ML's notation for appending two lists *)
fun elements LEAF = []
| elements (NODE (left, n, right)) =
elements left @ (n :: elements right)
(* o is ML's composition operation *)
val isort = elements o foldl insert' LEAF
(* uses binary-search tree for sorting *)
val result = isort [4,2,7,3,4,2,8,4,8,9];Check your understanding: ML Data Type Introduction
Consider the itree datatype declaration:
datatype itree = LEAF
| NODE of itree * int * itreeand the function elements
fun elements LEAF = []
| elements (NODE (left, n, right)) =
elements left @ (n :: elements right)If the elements function were applied to each of the following itree data structures, which would return the list [1,0,5]?
NODE (NODE (LEAF,0,LEAF),1,NODE (LEAF,5,LEAF))NODE (NODE (LEAF,5,LEAF),1,NODE (LEAF,0,LEAF))NODE (NODE (LEAF,1,LEAF),0,NODE (LEAF,5,LEAF))
Exceptions in ML
Example: Take from a list
(* Note use of exceptions. *)
(* And ; to sequence imperative operations *)
exception TooShort
fun take 0 _ = [] (* wildcard! *)
| take n [] = raise TooShort
| take n (x::xs) = x :: (take (n-1) xs)
val res5 = take 2 [1,2,3,4]
val res6 = take 3 [1]
handle TooShort =>
(print "List too short!"; [])Check your understanding: ML Exceptions
Recall the code for the take function:
exception TooShort
fun take 0 _ = [] (* wildcard! *)
| take n [] = raise TooShort
| take n (x::xs) = x :: (take (n-1) xs)and some code that exercises it:
val res5 = take 2 [1,2,3,4]
val res6 = take 3 [1]
handle TooShort =>
(print "List too short!"; [])Consider the partially-written function find which satisfies the following algebraic laws:
find p [] = raise NotFound
find p (x::xs) = x if p x
find p xs otherwise and some code that exercises it:
exception Blank1
fun find p [] = Blank2 NotFound
| find p (x::xs) =
if p x then x
else find p xs
val res = find even [1,3,5]
Blank3 NotFound => Blank4
Fill in the blanks to correctly complete the find function and return an answer of 0?
in a course-specific video or in some other medium.
14 Oct 2020: Programming with constructed data and types
There are PDF slides for 10/15/2020.
Handout: Learning ML
be two text answer boxes, one for the C/scheme answer and one for the ML answer.
Reflection: Defining new kinds of data
Suppose you were going to program a system to play card games in which suits (CLUBS, DIAMONDS, HEARTS, and SPADES) matter, such as poker, solitaire, bridge, or gin rummy. Briefly describe how you would represent the suits in C and in μScheme.
Now consider ML’s datatype mechanism that we used to define the itree type. Briefly describe how you could use ML’s datatype mechanism to represent suits.
Programming with Types
Foundation: Data
Syntax is always the presenting complaint, but data is what’s always important
“Language support for forms of data”
- Base types:
int,real,bool,char,string - Functions:
A -> B Constructed data:
- Tuples: pairs
A*B, triplesA*B*C, etc. - (Records with named fields)
- Lists and other algebraic types
Deconstruct using pattern matching
- Tuples: pairs
“Distinguish one cons cell (or one record) from another”
Lightweight constructed data: Tuples
Types defined wtih *: A1 * A2 * … * An
Expressions to create: (e1, e2, …, en)
Patterns to observe: (p1, p2, …, pn)
Example (splitList from merge sort):
let val (left, right) = splitList xs
in merge (sort left, sort right)
endEnumerated types
Datatypes can define an enumerated type and associated values.
datatype suit = HEARTS | DIAMONDS | SPADES | CLUBSHere suit is the name of a new type.
The value constructors HEARTS, DIAMONDS, SPADES, and CLUBS are the values of type suit.
Value constructors are separated by vertical bars.
Pattern matching
Datatypes are deconstructed using pattern matching.
fun toString HEARTS = "hearts"
| toString DIAMONDS = "diamonds"
| toString SPADES = "spades"
| toString CLUBS = "clubs"
val suitName = toString HEARTSCheck your understanding: Basic Datatypes
Consider the following partially written isRed function that is supposed to determine if a given suit is one of the two red suits (ie, is either a heart or a diamond).
fun isRed HEART = BLANK1
| BLANK2 BLANK3 = true
| isRed _ = falseBut wait, there’s more: Value constructors can take arguments!
datatype int_tree =
LEAF | NODE of int * int_tree * int_treeint_tree is the name of a new type.
There are two data constructors: LEAF and NODE.
NODEs take a tuple of three arguments: a value at the node, and left and right subtrees.
The keyword of separates the name of the data constructor and the type of its argument.
When fully applied, data constructors have the type of the defining datatype (ie, int_tree).
It’s recursive!
Building values with constructors
We build values of type int_tree using the associated constructors:
val tempty = LEAF
val t1 = NODE (1, tempty, tempty)
val t2 = NODE (2, t1, t1)
val t3 = NODE (3, t2, t2)What is the in-order traversal of t3?
[1,2,1,3,1,2,1]What is the pre-order traversal of t3?
[3,2,1,1,2,1,1]Deconstruct values with pattern matching
(The @ symbol denotes append in ML)
fun inOrder LEAF = []
| inOrder (NODE (v, left, right)) =
inOrder left @ [v] @ inOrder right
val il3 = inOrder t3
fun preOrder LEAF = []
| preOrder (NODE (v, left, right)) =
v :: preOrder left @ preOrder right
val pl3 = preOrder t3Reflection: How general is the code?
Consider the int_tree datatype and the code we’ve written to manipulate it:
datatype int_tree =
LEAF | NODE of int * int_tree * int_tree
fun inOrder LEAF = []
| inOrder (NODE (v, left, right)) =
inOrder left @ [v] @ inOrder right
fun preOrder LEAF = []
| preOrder (NODE (v, left, right)) =
v :: preOrder left @ preOrder rightDiscuss the extent to which this code requires the value stored at each node to be an integer. Type errors aside, would the code still work if we stored a different kind of value in the tree?
But wait, there’s still more: Polymorphic datatypes!
int_tree is monomorphic because it has a single type.
Note though that the inOrder and preOrder functions only cared about the structure of the tree, not the payload value at each node.
Polymorphic datatypes are written using type variables that can be instantiated with any type.
datatype 'a tree =
CHILD | PARENT of 'a * 'a tree * 'a treetree is a type constructor (written in post-fix notation), which means it produces a type when applied to a type argument.
Examples:
int treeis a tree of integersbool treeis a tree of booleanschar treeis a tree of charactersint list treeis a tree of a list of integers.
'a is a type variable: it can represent any type.
It is introduced on the left-hand of the = sign. References on the right-hand side are types.
CHILD and PARENT are value constructors.
CHILD takes no arguments, and so has type 'a tree
When given a value of type 'a and two 'a trees, PARENT produces a 'a tree
Constructors build tree values
val empty = CHILD
val tint1 = PARENT (1, empty, empty)
val tint2 = PARENT (2, tint1, tint1)
val tint3 = PARENT (3, tint2, tint2)
val tstr1 = PARENT ("a", empty, empty)
val tstr2 = PARENT ("b", tstr1, tstr1)
val tstr3 = PARENT ("c", tstr2, tstr2)Pattern matching deconstructs tree values
fun inOrder CHILD = []
| inOrder (PARENT (v, left, right)) =
(inOrder left) @ [v] @ (inOrder right)
fun preOrder CHILD = []
| preOrder (Parent (v, left, right)) =
v :: (preOrder left) @ (preOrder right)Functions inOrder and preOrder are polymorphic: they work on any value of type 'a tree. 'a is a type variable and can be replaced with any type.
Environments
Datatype definitions introduce names into:
the type environment:
suit,int_tree,treethe value environment:
HEART,LEAF,PARENT
Inductive
Datatype definitions inherently inductive:
the type
int_treeappears in its own definitionthe type
treeappears in its own definition
Check your understanding: Defining Datatypes
We can define a subset of the S-expressions in Scheme using the following specification:
An SX1 is either an ATOM or a list of SX1s, where ATOM is represented by the ML type atom.
Complete the encoding of this definition by filling in the blanks in the following ML datatype:
datatype sx1 = ATOM of BLANK1
| LIST of BLANK2 listAnother way of defining a subset of the S-expressions in Scheme uses a different specification:
An SX2 is either an ATOM or the result of consing together two values v1 and v2, where both v1 and v2 are themselves members of the set SX2.
Complete the encoding of this definition by filling in the blanks in the following ML datatype:
datatype sx2 = ATOM of BLANK1
| PAIR of BLANK2 BLANK3 BLANK4Coding interlude: Defining a datatype
Designing a datatype is a three step process:
- For each form, choose a value constructor
- Identify the “parts” type that each constructor is
of - Write the datatype definition
Another definition of a Scheme S-expression is that it is one of:
- A symbol (string)
- A number (int)
- A Boolean (bool)
- A list of S-expressions
Define an ML datatype sx that encodes this version of an S-expression.
Making types work for you
Type-directed programming
Common idea in functional programming: lifting
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)The type of a function tells us a lot about how to write it—the type often narrows the code down to a very few sensible choices. This technique works especially well with polymorphic functions.
Here’s the problem we’re going to solve: we have a predicate on single elements, and we want a predicate on lists of elements:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)And here is the main tool we are going to use: for every type, we are going to be aware of how to make a value of the type (its introduction form) and what we can do with a value of the type (its elimination form).
Let’s review for the types we have:
Arrow types: A function of any type can always be create with an explicit lambda (
fn). And the only thing we can do with a function is apply it.Boolean: can make Booleans with
trueandfalse. We can use them inifexpressions and we can pattern match on them.List types: Any value of list type is always made with
::.
And to take one apart, we use pattern matching (incaseorfun).The unknown type
'a: We have to be prepared for any'aat all, so there’s no syntax that goes with it. InsteadIf we want an expression of unknown type
'a, our choices are that we have a variable of'a(maybe a parameter), or maybe we can apply a function that returns a value of'a.All we can do with a value of unknown type are the things we can do with any type: pass it to functions or store it in data structures.
Table:
Type Intro Elim
... -> ... fn application
bool true, false if, pattern matching (case/fun)
... list [], :: pattern matching (case/fun)
'a --- ---Let’s get started: our goal is to make a function of type
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)We can always use fun
fun lift p = _goal1Q: What is the type of p? How do we know?
Q: What is the type of _goal1? How do we know?
Answers:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) = (_goal1 : 'a list -> bool)Our new goal is a term of type 'a list -> bool. Which of these forms of expression is always safe and makes progress toward a goal of this type?
- A recursive call
- A lambda expression of the form
(fn ... => ...) - A
letexpression
Our goal is an arrow type, and it is always safe to make a value of arrow type using lambda:
_goal1 = (fn xs => _goal2)
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) = (fn xs => _goal2)Q: What is the type of xs? How do we know?
Q: What is the type of _goal2? How do we know?
Answers:
_goal1 = (fn xs => _goal2)
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) = (fn (xs : 'a list) => (_goal2 : bool))Things we have
lift : ('a -> bool) -> ('a list -> bool) [it could call itself recursively]
p : 'a -> bool
xs : 'a listNow we have a goal of type bool and we want to use the parameter xs of type 'a list. What is the safest tactic to make progress using xs?
- Break it down by cases, that is, ask whether it is nil or cons
- Pass it to
foldlorfoldr - Pass it to
lift p
Now we have a new goal of type bool. And we know two ways to make a value of type bool: we can return true or false. But if we choose true or false, we will have defined a function that is not very interesting, and we will have completely ignored all the parameters to lift. That is probably not a great design choice.
Is there some other way to make a bool? Some way to use what we have?
Our
phas type'a -> bool, and that’s an arrow type, so the only thing we can do with it is apply it. But we don’t have a value of'ato apply it to. Let’s set it aside.Our
xshas type'a list. This doesn’t solve our immediate goal of abool, but since it’s a list, we can try to take it apart. We knowxsis either nil or cons. So let’s fill the hold [goal2] with acaseexpression.
Next take:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) =
fn (xs : 'a list) =>
case xs
of [ ] => _goal3 : bool
| y :: ys => _goal4 : boolNow instead of one hole we have two holes, each of type bool. But we have used xs, so that’s progress. What’s next? Let’s look at the first hole.
This first hole still has type bool. And we now know that xs is empty, so we have used all the information available in xs, but we still haven’t used p. Which of the following tactics is viable for fulfilling our goal of type bool? Mark all that apply.
- Look for a value of type
'ato applypto - Give up on
pand fill the hole withtrue - Give up on
pand fill the hole withfalse
The hole
_goal3has a typebool. We know everything available to be known aboutxs(namely, it’s empty). All we have left isp.And
phas type'a -> bool, with no prospect of'ato apply it to. But we have to fill the hole.Our only choices are
trueandfalse. Which would you like to pick?
Let’s flip a coin. My coin comes up true. So now we have
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) =
fn (xs : 'a list) =>
case xs
of [ ] => true
| y :: ys => _goal4 : boolOur final goal has type bool, but now we have more Booleans than we know what to do with: both p y and lift p ys. What answer best describes what we should do?
- Ignore
p yand fill the hole withlift p ys - Ignore
lift p ysand fill the hole withp y - Combine the two Booleans using
andalso - Combine the two Booleans using
orelse - Two Booleans can be combined in 16 different ways, and they are all equally good.
We have to fill that last hole. And we have new variables y and ys. What are their types? How do we know?
y : 'a
ys : 'a listAdd them to everything we have and it’s now
lift : ('a -> bool) -> ('a list -> bool)
p : 'a -> bool
y : 'a
ys : 'a listHow can we use y and ys?
We can apply
p yand that’s an expression ofbool.But we’d also like to use
ys.Q: Can we use
ys?A: Yes! We can all
lift precursively. We know it terminates because the list argument keeps getting smaller.
So now these are the things we have:
lift : ('a -> bool) -> ('a list -> bool)
p : 'a -> bool
y : 'a
ys : 'a list
p y : bool
lift p ys : boolWe have just one hole to fill, but we have two terms of type bool. If we want to use all our information, both y and ys, we’d better combine them.
Q: What are common ways to combine two Booleans?
A: Two good ways are andalso and orelse.
Q: Which one do you like here?
A: Let’s think about both choices:
Q: Suppose we pick
orelsehere. How doesliftbehave?A: It always returns
trueQ: Suppose we pick
andalsohere. How doesliftbehave?A: Hey! It behaves just like the
allfunction! I know that function!
Q: Nice. And here it is:
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift (p : 'a -> bool) =
fn (xs : 'a list) =>
case xs
of [ ] => true
| y :: ys => p y andalso lift p ysOr if we pretty it up a little,
val lift : forall 'a . ('a -> bool) -> ('a list -> bool)
fun lift p xs =
case xs
of [ ] => true
| y :: ys => p y andalso lift p ysor even
fun lift p [] = true
| lift p (y :: ys) = p y andalso lift p ysMaking types work for you: The false case
Q: Suppose back at the empty-list step, the coin had come down differently and we had used true there. What would we want to do then?
A: I know this one! We combine two Booleans with orelse instead of andalso! That’s the exists function!
Q: Indeed:
fun lift' p [] = false
| lift' p (y :: ys) = p y orelse lift p ysPotential bonus content: inorder traversal of binary tree.
val find : forall 'a . ('a -> bool) -> ('a list -> 'a option)Additional language support for algebraic types: case expressions
Bonus content: Exceptions — Handling unusual circumstances
Syntax:
- Definition:
exception EmptyQueue - Introduction:
raise ewheree : exn - Elimination:
e1 handle pat => e2
Informal Semantics:
- alternative to normal termination
- can happen to any expression
- tied to function call
- if evaluation of body raises exn, call raises exn
Handler uses pattern matching
e handle pat1 => e1 | pat2 => e2
Bonus Content: A different explanation of ML Datatypes
Tidbits:
The most important idea in ML!
Originated with Hope (Burstall, MacQueen, Sannella), in the same lab as ML, at the same time (Edinburgh!)
Notes:
A “suit” is constructed using
HEARTS,DIAMONDS,CLUBS, orSPADESA “list of A” is constructed using
nilora :: as, whereais an A andasis a “list of A”A “heap of A” is either empty or it’s an A and two child heaps
Exegesis (on board):
Notation
'ais a type variable- On left-hand side, it is a formal type parameter
- On right-hand side it is an ordinary type
- In both cases it represents a single unknown type
Name before
=introduces a new type constructor into the type environment. Type constructors may be nullary.Alternatives separated by bars are value constructors of the type
They are new and hide previous names
(Do not hide built-in names
nilandlistfrom the initial basis!)Value constructors build constructed data
Value constructors participate in pattern matching
Complete by themselves:
HEARTS,SPADES,nilExpect parameters to make a value or pattern:
::,HEAPThe value a constructor is applied to is said to be carried
Every
valon this slide is a value constructoropenables an infix operator to appear in a nonfix contextType application is postfix
- A list of integer lists is written:
int list list
- A list of integer lists is written:
New names into two environments:
suit,list,heapstand for new type constructorsHEARTS,CLUBS,nil,::,EHEAP,HEAPstand for new value constructors
Algebraic datatypes are inherently inductive (
listappears in its own definition)—to you, that means finite trees'a * 'a listis a pair type — infix operators are always applied to pairs
Bonus Content: ML traps and pitfalls
Bonus content (seen in examples)
Syntactic sugar for lists
Bonus content: ML from 10,000 feet
Environments
Patterns
Functions
Tuples are “usual and customary.”
Types
19 Oct 2020: Types
There are PDF slides for 10/20/2020.
Retrospective: Evaluating ML
You are now in a position to start to evaluate ML.
Please enter at least one strength of ML.
Please enter at least one weakness of ML.
Your answers may be anonymously shared with your classmates.
Reflection: Catching errors with types
We have seen that one of the key differences between μScheme and ML is that ML has a static type system. One of the key roles of a type system is to detect errors. List at least two kinds of errors that type systems can detect at compile time (Hint: think about the kinds of type errors the ML compiler complains about).
Type systems aren’t omniscient, though. Now list at least one kind of error that ML’s type system can’t find and do your best to explain why it can’t.
Where type systems are found:
- C#, Swift, Go
- Java, Scala, Rust (polymorphism)
- ML, Haskell, TypeScript, Hack (inference)
Our trajectory:
- Formalize familiar, monomorphic type systems (like C)
- Learn polymorphic type systems
- Eventually, infer polymorphic types
Monomorphic types systems are the past.
Inference and polymorphism are the present and future.
(Visible trend just like lambda.)
This “lecture”:
- Formal type system with only two types:
words andflags
- Type checker derived from inference rules
Next time:
- Unbounded number of types! (Formation, introduction, elimination)
Type systems
What kind of thing is it?
Questions type systems can answer:
What kind of value does it evaluate to (if it terminates)?
What is the contract of the function?
Is each function called with the right number of arguments?
(And similar errors)Who has the rights to look at it/change it?
Is the number miles or millimeters?
Questions type systems typically do not answer:
Can it divide by zero?
Can it access an array out of bounds?
Can it take the
carof'()?Will it terminate?
Decidability and Type Checking
Suppose L is a Turing-Complete Language.
P is the set of programs in L that terminate.
Wish: a type system to statically classify terminating programs:
Expression e in L has type T (e : T) iff e terminates.
But: Undecideable!
We can prove no such type system exists. (See Comp170 for the Halting Problem)
Choices:
Allow type checker to run forever.
Don’t use type system to track termination.
Static vs. Dynamic Type Checking
Most languages use a combination of static and dynamic checks
Static: “for all inputs”
- input independent
- efficient at run-time
- approximate : rules out some programs that won’t trigger errors
example:(if false then 2 else "hi") ^ "there"
Dynamic: “for some inputs”
- depends on input
- run-time overhead
- precise
Check your understanding: Static vs. Dynamic Type Systems
Type systems can statically detect all errors.
- True
- False
Static type systems generally use a combiniation of static and dynamic checks.
- True
- False
Dynamic type systems impose runtime overhead.
- True
- False
Type System and Checker for a Simple Language
Why do we write a type checker?
Canonical example of static analysis. Used pervasively in industry in code improvement and security analysis.
Great practice connecting math to code. To be educated about programming languages, you must be able to realize inference rules in code. Eventually you should learn to “speak” inference rules like a native. Implementing a type system is a valuable way to build these competencies.
Tool for structuring language design, which applies to input validation. If (when!) you get to do your own language designs, type systems are an area where you are most likely to be able to innovate. The ideas behind type systems apply any time you need to validate user input, for example. This is the highest level of cognitive task: creation of new things.
Examples to rule out
Can’t add a word and a flag:
3 + (3 < 99)
(ARITH(PLUS, LIT 3, CMP (LT, LIT 3, LIT 99)))Can’t compare a word and a flag
(3 < (4 = 24))
CMP (LT, LIT 3, CMP(EQ (LIT 4, LIT 24)))Check your understanding: AST Representation of Simple Language
Recall the AST for the simple machine language:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| LIT of int
| IF of exp * exp * exp
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = WORDTY | FLAGTYThe AST term
CMP(GT, (CMP(EQ, LIT 105, LIT 170)), LIT 160)
which encodes the expression
((105 = 170) > 160)
should be flagged as a type error.
- True
- False
Inference rules to define a type system
Form of judgment Context
|-term:typeWritten
|- e : tauContexts vary between type systems
(Right now, the empty context)
Judgment is proved by derivation
Derivation made using inference rules
Inference rules determine how to code
val typeof : exp -> ty:Given
e, findtausuch that|- e : tau
Rule for arithmetic operators
Informal example:
|- 3 : word |- 5 : word
-------------------------
|- 3 + 5 : wordRules out:
|- 'a' : char |- 5 : word
---------------------------
|- 'a' + 5 : ???General form:
|- e1 : word |- e2 : word
-----------------------------
|- ARITH ( _ , e1, e2) : wordRule for comparisons
Informal example:
|- 7 : word |- 10 : word
-----------------------------
|- 7 < 10 : flagGeneral form:
|- e1 : word |- e2 : word
-----------------------------
|- CMP ( _ , e1, e2) : flagRule for literals
Informal example:
|- 14 : wordGeneral form:
--------------------
|- LIT (n) : wordRule for conditionals:
Informal example:
|- true : flag
|- 3 : word
|- 42 : word
--------------------------
|- IF (true, 3, 42) : wordGeneral form:
|- e : flag
|- e1 : tau1
|- e2 : tau2 tau1 equiv tau2
-----------------------------------
|- IF ( e, e1, e2) : tau1Typing rules let us read off what a type checker needs to do.
input to checker: e
output from checker: tau
Type checker in ML
val typeof : exp -> ty
exception IllTyped
fun typeof (ARITH (_, e1, e2)) =
case (typeof e1, typeof e2)
of (WORDTY, WORDTY) => WORDTY
| _ => raise IllTyped
| typeof (CMP (_, e1, e2)) =
case (typeof e1, typeof e2)
of (WORDTY, WORDTY) => FLAGTY
| _ => raise IllTyped
| typeof (LIT _) = WORDTY
| typeof (IF (e,e1,e2)) =
case (typeof e, typeof e1, typeof e2)
of (FLAGTY, tau1, tau2) =>
if eqType (tau1, tau2)
then tau1 else raise IllTyped
| _ => raise IllTypedCheck your understanding: A type checker from inference rules
Recall the AST for the simple machine language:
datatype exp = ARITH of arithop * exp * exp
| CMP of relop * exp * exp
| LIT of int
| IF of exp * exp * exp
and arithop = PLUS | MINUS | TIMES | ...
and relop = EQ | NE | LT | LE | GT | GE
datatype ty = WORDTY | FLAGTYand the inference rule for comparisons:
|- e1 : word |- e2 : word
-----------------------------
|- CMP ( _ , e1, e2) : flag
and our in-progress type checking code typeof
val typeof : exp -> ty
exception IllTyped
fun typeof (ARITH (_, e1, e2)) =
case (typeof e1, typeof e2)
of (WORDTY, WORDTY) => WORDTY
| _ => raise IllTyped
| typeof (CMP (_, e1, e2)) =
case (BLANK1, BLANK2)
of (BLANK3, BLANK4) => BLANK5
| _ => raise IllTyped
| typeof (LIT _) = WORDTY
| typeof (IF (e,e1,e2)) =
case (typeof e, typeof e1, typeof e2)
of (FLAGTY, tau1, tau2) =>
if eqType (tau1, tau2)
then tau1 else raise IllTyped
| _ => raise IllTyped
Fill in the blanks based on the comparison inference rule to complete the code for the CMP case.
An implementor’s trick: If you see identical types in a rule,
Give each type a distinct subscript
Introduce equality constraints
Remember to be careful using primitive equality to check types—you are better off with
eqType.
Typing Rules: Contexts and Term Variables
What could go wrong with a variable?
Used inconsistently:
;; x can’t be both an integer and a list
x + x @ x
;; y can’t be both an integer and a string
let y = 10 in y ^ “hello” end
So we need to track variable use to ensure consistency
Key idea: Type environment (Gamma) tracks the types of variables.
Rule for var
x in dom Gamma tau = Gamma(x)
----------------------------------------
Gamma |- VAR x : tauSo as long as x is recorded in Gamma as a WORDTY, it can only be used as a WORDTY.
Rule for let
Gamma |- e1 : tau1
Gamma{x->tau1} |- e2 : tau2
-------------------------------------
Gamma |- LET x = e1 in e2 : tau2Type Checker
Type checker needs Gamma – gives type of each “term variable”.
Check your understanding: Adding variables
Given the typing rule for the let form we added to the simple machine language:
Gamma |- e1 : tau1
Gamma{x->tau1} |- e2 : tau2
-------------------------------------
Gamma |- LET x = e1 in e2 : tau2Fill in the missing blanks to complete the type checker we started in the video:
val typeof : exp * ty env -> ty
fun typeof (ARITH ..., Gamma ) = <as before>
| typeof (VAR x, Gamma) =
(case maybeFind (x, Gamma)
of SOME tau => tau
| NONE => raise IllTyped)
| typeof (LET (x, e1, e2), Gamma) =
let tau1 = typeof (BLANK1, BLANK2)
in BLANK3 (BLANK4, extend Gamma x BLANK5)
end
Taking Stock
I gave you syntax for simple language.
We came up with formal typing rules.
We used the typing rules to implement the type checker.
On your homework,
You will design new syntax and typing rules for lists
You will extend an existing type checker
You will implement a full type checker from scratch
This is a big chunk of what language designers do.
Bonus content
What is a type?
Weak: a set of values
Better: a conservative prediction about values
Best: the precise definition: classifier for terms!!
The relationship to values becomes a proof obligation.
Note: a computation can have a type even if it doesn’t terminate! (Or doesn’t produce a value)
Source of new language ideas for next 20 years
Needed if you want to understand advanced designs (or create your own)
What types can rule out
things that could go wrong:
(8 < 10) + 4
(8 == 8) < 9
x + (x :: xs)
let val y = 10 in length y end21 October 2020: Type checking with type constructors
There are PDF slides for 10/22/2020.
should have two separate answer boxes: one for what they have learned and one for what they have questions about.
Reflection: Simple type checking
In the first part of this module on type checking, we talked about the purposes and limitations of type systems, we formalized a simple type system with just two types using inference rules, and we converted those inference rules into a type checker.
Describe two specific things you have learned so far in this module.
Write one question you have about what we’ve learned so far.
Your responses may be shared anonymously with your classmates.
Reflection: How many types?
In the previous “lecture”, we studied a type system with just two types: words and flags. In this “lecture”, we’re going to add type constructors such as function types and lists. When we ``add lists" to a language, how many types are we adding?
Where we’ve been
New watershed in the homework
You’ve been developing and polishing programming skills: recursion, higher-order functions, using types to your advantage. But the problems have been mostly simple problems around simple data structures, mostly lists.
You’ve already seen everything you need to know to implement a basic type checker, and you are almost fully equipped to add array operations and types to Typed Impcore.
Where we’re going
We’re now going to shift and spend the next several weeks doing real programming-languages stuff, starting with type systems.
What’s next is much more sophisticated type systems, with an infinite number of types.
Focus on two questions about type systems:
What is and is not a good type, that is, a classifier for terms?
How shall we represent types?
We’ll look at these questions in two contexts: monomorphic (this “lecture”) and polymorphic (next “lecture”) languages.
Monomorphic vs Polymorphic Types
Monomorphic types have “one shape.”
- Examples:
int,bool,int -> bool,int * int
Polymorphic types have “many shapes.”
Examples:
(forall ('a) (list 'a)) (forall ('a) ((list 'a) -> int)) (forall ('a) ((list 'a) -> (list 'a)))Substitute any type you like for
'a.ML Examples:
'a list,'a list -> int,'a list -> 'a listIn ML,
forallis only at the top level, and it isn’t written explicitly
Designing monomorphic type systems
Mechanisms:
Every new variety of type requires special syntax (examples: structs, pointers, arrays)
Implementation is a straightforward application of what you already know.
Language designer’s process:
What new types do I have?
- Formation rules
How do I create new values with that type?
- Introduction rules
For introduce think “produce”, “create”, “make”, “define”
What new syntax do I have to observe terms of a type?
- Elimination rules
For eliminate think “consume”, “examine”, “interrogate”, “look inside”, or “take apart”, “observe”, “use”, “mutate”
Words “introduce” and “eliminate” are the native vocabulary of type-theoretic language design—it’s like knowing what to say when somebody sneezes.
Managing the set of types: Type formation
Check your understanding: Types, type constructors, or garbage
In each of the following, indicate whether the “type” is in fact a type (ie, something that classifies terms), a type constructor (ie, something that will classify terms when applied to some number of type arguments), or utter nonsense.
bool list
- type
- type constructor
- utter nonsense
array
- type
- type constructor
- utter nonsense
bool bool
- type
- type constructor
- utter nonsense
->
- type
- type constructor
- utter nonsense
These rules are actually the same as we saw for the simple arithmetic language, but we’ll review them again here.
Monomorphic type rules
Check your understanding: Checking type equalities
We saw how to modify the typing rule for Set to explicitly mark where two types were being compared for equality. The typing rule for If that we saw in the video has a similar implicit type equality check. Fill in the missing blanks in the typing rule below to create a version with an explicit equality check.
Classic types for data structures
At run time, these pairs are identical to cons, car, cdr.
These rules dictate type checker code just like in previous “lecture”.
Check your understanding: Writing Typing Rules
ML References are similar to C/C++ pointers. Given the following surface syntax (on the left) and corresponding AST represenations (on the right):
| Surface Syntax | AST |
|---|---|
ref τ |
ref(τ) |
ref e |
ref-make(e) |
!e |
ref-get(e) |
e1 := e2 |
ref-set(e1,e2) |
fill in the blanks to correctly complete the following formation, introduction, and elimination rules.
=10ptBonus Content
Coding the arrow-introduction rule
Approaching types as programmers
Talking type theory: Introduction and elimination constructs
Part of learning any new field: talk to people in their native vocabulary
Introduce means “produce”, “create”, “make”, “define”
Eliminate means “consume”, “examine”, “observe”, “use”, “mutate”
It’s like knowing what to say when somebody sneezes.
Type soundness
26 Oct 2020: Polymorphic Type Checking
There are PDF slides for 10/27/2020.
Your type-system questions are answered.
Today
- Burdens of monomorphism
- On designers and implementors
- On programmers
- Lift burden with quantified types
- Extensible type formation
Reflection: Type checking type constructors
In the previous two “lectures” we studied how to type check a known set of types. In each case, the syntax for the type was hard-coded into the AST for the language. Type checking the creation and uses of values with the type were also hard-coded into the type checker. That approach works fine if the language designers know all the types in advance. But, in any language worth its salt, programmers can create new types, (for example, by defining algebraic datatypes in ML, structs in C, or classes in Java). The language has to be able to type check these new types without having to recompile the language implementation first.
Spend a few minutes thinking about how we might redesign the implementation of the type checker to accommodate user-defined types.
Describe your preliminary design in a few sentences.
Limitations of monomorphic type systems
Notes:
- Implementing arrays on homework
- Writing rules for lists on homework
Check your understanding: Monomorphism limitations
If a language has a monomorphic type system, it will not let programmers write a single length function for lists. Instead, programmers must write a length function for each kind of list they want to calculate the length of, eg, a length function for lists of booleans, and another for lists of integers, etc.
- True
- False
Quantified types
Check your understanding: Quantified Types
The type theory expression and the expression are two different representations for the same polymorphic type.
- True
- False
In the type (forall ('a) ([list 'a] -> 'a)), the notation 'a denotes a type variable that stands for the type of element in the list argument and the type of the result returned by the function.
- True
- False
The type (forall ('a) ([list 'a] -> [list 'a])) is the type of the car function.
- True
- False
Bonus instantiation:
-> map
<function> :
(forall ['a 'b]
(('a -> 'b) (list 'a) -> (list 'b)))
-> [@ map int bool]
<function> :
((int -> bool) (list int) -> (list bool))Two forms of abstraction:
Coding Interlude: Instantiating Polymorphic Functions
Enter the length function into the interpreter to observe its type.
Apply the length function to the list [1,2,3]. Observe the response.
Create two instantiations of the length function: one for ints and one for bools.
Apply the length-int function to the list [1,2,3] and the length-bool function to the list [#t, #f] and observe the result.
What do you see as the advantages and disadvantages of ’s approach to polymorphism so far?
Polymorphic Type Checking
Representing quantified types
Check your understanding: Representation of quantified types
Given the tyex datatype:
datatype tyex
= TYCON of name // int
| CONAPP of tyex * tyex list // (list bool)
| FUNTY of tyex list * tyex // (int int -> bool)
| TYVAR of name // 'a
| FORALL of name list * tyex // (forall ('a) ...)Match the surface syntax for polymorphic types with their representations using the tyex datatype.
Surface syntax:
bool'a(list int)(bool bool -> int)(forall ['b] ((list 'b) -> int))
Represenation:
FUNTY ([TYCON "bool", TYCON "bool"], TYCON "int")TYVAR "a"FORALL ("b", FUNTY ([CONAPP (TYCON "list", [TYVAR "b"])], TYCON "int"))TYCON "bool"CONAPP (TYCON "list", [TYCON "int"])
Type rules for polymorphism
Check your understanding: Rules for type-lambda
- In the new judgement form for type checking
type-lambda, the meta-variable Δ is a kind environment that records the type variables that have been used in typing a program.
- True
- False
- The AST term tylambda(α1,…,αn, e) is the representation of the surface syntax
(@ eτ1...τn)
- True
- False
- In the introduction rule for
type-lambda, it is okay if the type variables to be quantified over already appear in the context Γ.
- True
- False
- In the elimination rule for
type-lambda, the resulting type is obtained by substituting the type arguments for the corresponding quantified type variables. If the type of the expression e is quantified over m type variables and e is applied to n type arguments, a type error should result if n ≠ m.
- True
- False
Type formation through kinds
Check your understanding: Use kinds to classify types
For each type expression, select its kind or indicate it is not well formed.
char
** => *- not well defined
list list
** => *- not well defined
array
** => *- not well defined
Opening the closed world
Bonus content: a definition manipulates three environments
28 October 2020: Introduction to type inference
There are PDF slides for 10/29/2020.
Retrospective: Type Checking
Write one thing you learned in the previous module about type checking and one question you have about that material.
Your responses may be anonymously shared with the rest of the class.
Reflection: How does the compiler know?
Consider the following ML code for the append function:
fun append (x::xs) ys = x :: append xs ys
| append [] ys = ysWhen you enter this code into the ML comiler, it returns the type of the function.
Describe how you think the ML compiler might figure out the type of the function.
Let’s do some examples
N.B. Book is “constraints first;” lecture will be “type system first.” Use whatever way works for you
Example: (val-rec double (lambda (x) (+ x x)))
What do we know?
doublehas type ′a1xhas type ′a2+has typeint * int -> int(+ x x)is an application, what does it require?- ′a2 ~
intand ′a2 ~int
- ′a2 ~
Is this possible?
Key idea: Record the constraint in a typing judgement.
'a2 ~ int /\ 'a2 ~ int,
{ double : 'a1, x : 'a2 } |- (+ x x) : intExample: (if y 1 0)
yhas type ′a3,1has typeint,0has typeintRequires what constraints? (
int~int, ′a3 ~bool)
Example: (if z z (- 0 z))
zhas type ′a3,0has typeint,-has typeint * int -> intRequires what constraints? (′a3 ~
bool/\int~int/\′a3 ~int)These constraints are not solveable so the program is ill-typed.
Check your understanding: Gathering constraints
- In this judgment
'ax ~ int /\ 'ay ~ int,
{x : 'ax, y : 'ay } |- (+ x y) : intthe notation 'ay ~ int is a constraint that means that the type variable 'ay must be equal to type int.
- True
- False
- In this judgment
'ax ~ int /\ 'ay ~ int,
{x : 'ax, y : 'ay } |- (+ x y) : intthe notation y : 'ay means that expression variable y has type 'ay. Furthermore, because y has a type variable for its type, y’s type can become any syntactically valid type.
- True
- False
- Which set of constraints might have been generated when running type inference on the following program fragment? Pick the most complete set that applies.
(if x (+ 1 y) z)
'ax~'ay,'ay~int,'az~int'ax~bool,'ay~int,'az~int'ax~'ay,'ay~'az'ay~int,'az~int'ax~bool,'ay~int
Inferring polymorphic types
(val app2 (lambda (f x y)
(begin
(f x)
(f y))))Assume f : 'a_f
Assume x : 'a_x
Assume y : 'a_y
f x implies 'a_f ~ ('a_x -> 'a1)
f y implies 'a_f ~ ('a_y -> 'a2)
Together, these constraints imply 'a_x ~ 'a_y and 'a1 ~ 'a2
begin implies result of function is 'a2
So,
app2 : (('a_x -> 'a2) 'a_x 'a_x -> 'a2)'a_x and 'a2 aren’t mentioned anywhere else in program, so
we can generalize to:
(forall ('a_x 'a2) (('a_x -> 'a2) 'a_x 'a_x -> 'a2))which is the same thing as:
app2 : (forall ('a 'b) (('a -> 'b) 'a 'a -> 'b))Check your understanding: Type inference with polymorphic functions
This question walks you through generating constraints for a simple function that makes two calls to a polymorphic function. It illustrates how those two calls can end up being used at different types.
Each subquestion builds on the previous one. The explanations given after each subquestion explain what you need to know for the next part.
Consider the following program:
(val cc (lambda (nss) (car_2 (car_1 nss))))where car_1 and car_2 are two instances of the polymorphic car function that has type
car : forall 'a . 'a list -> 'aFor the purposes of this question we’ve named these uses car_1 and car_2 so we can be clear which use we are talking about as we study their effect on the type of the expression.
Variable
nssis a parameter, and so during type checking, we assign it a fresh type variable, say'b.- True
- False
- We need to instantiate the two instances of the polymorphic
carfunction before we can apply them. Which set of instantiations is correct?
car_1 : 'a1 list -> 'a1andcar_2 : 'a1 list -> 'a1car_1 : 'a1 list -> 'a2andcar_2 : 'a2 list -> 'a1car_1 : 'a2 list -> 'a1andcar_2 : 'a1 list -> 'a2car_1 : 'a1 list -> 'a1andcar_2 : 'a2 list -> 'a2
- Given what we have already inferred about the types of
car_1andnss(and given in the answers in parts 1 and 2), which of the following constraints is generated by the application(car_1 nss)?
'b ~ 'a1'b ~ 'a1 list'a1 ~ 'a2 list'b ~ 'a2 list
- Given what we have already inferred about the types of
car_1,car_2, andnss(and given in the answers in parts 1, 2, and 3), which of the following constraints is generated by the application of the functioncar_2to the argument(car_1 nss)in the term(car_2 (car_1 nss)):
'a2 ~ 'a1'a2 ~ 'a1 list'b ~ 'a2'a1 ~ 'a2 list
Extra examples
Precise inference with Hindley-Milner types
To code the type-inference algorithm, replace eqType with constraint generation!
Check your understanding: Hindley-Milner Types
- With Hindley-Milner types, the meta-variable τ cannot stand for a type variable α.
- True
- False
- With Hindley-Milner types, the meta-variable σ represents a polymorphic type and has the form ∀ α1,… αn . τ.
- True
- False
- Choose the appropriate values for the blanks in the following ML data structure to make it represent the the Hindley-Miler type scheme ∀ α . α list -> α.
FORALL (BLANK1,
CONAPP(BLANK2,
[CONAPP (TYCON "arguments", BLANK3),
TYVAR "alpha" ]))BLANK1:
- “alpha”
- [“alpha”]
- TYVAR “alpha”
BLANK2:
- TYCON “function”
- [TYCON “function”]
- “function”
BLANK3:
- CONAPP(TYCON “list”, [TYVAR “alpha”])
- CONAPP(“list”, [TYVAR “alpha”])
- CONAPP(TYCON “list”, TYVAR “alpha”)
- CONAPP(“list”, “alpha”)
- In Hindley-Miler type inference, type environments Γ always bind variables to type scheme σ. If a variable is monomorphic, the type scheme will quantify over an empty list of type variables (ie, be of the form ∀ . τ)
- True
- False
- Match each step in Hindley-Milner type inference with its purpose.
Steps:
- constraint generation
- constraint solving
- substitution
- generaliation
- instantiation
Purposes:
- Refining types based on information inferred during constraint solving.
- Collating clues to make sure expressions are used consistently.
- Converting type scheme into a type so that it may be used in a given context.
- Collecting clues about how expressions are used in the program.
- Introducing type scheme to memorialize inference that given expression will work for any type.
2 November 2020: Making type inference formal
There are PDF slides for 11/3/2020.
Retrospective: Introduction to type inference
Write one thing you learned about type inference so far and one question you have. Your answers may be anonymously shared with your classmates.
Type inference algorithm, formally
Apply rule: e’s type could just be a type variable—we need to force it into the arrow form we need.
What you know and can do now
Check your understanding: Type inference algorithm
- The judgment form C, Γ |- e : τ corresponds to the function
typeof. For each element of the judgment, say whether that element is an input or an output of the functiontypeof:
Constraint C:
- input
- output
Context Γ:
- input
- output
Expression e:
- input
- output
Type τ:
- input
- output
- Consider the typing rule for apply written in the new style:
Now answer the following questions about the rule.
A. The type τf is the type of the first argument to the function being applied.
- True
- False
B. The arguments to the function e1, …, en have types τ1, … τn, respectively.
- True
- False
C. The type variable α is the result type of the function.
- True
- False
Reflection: Solving constraints
For each of the following constraints, say if it is solvable. If it is, give a solution.
1. int ~ bool
2. (list int) ~ (list bool)
3. 'a ~ int
4. 'a ~ (list int)
5. 'a ~ ((args int) -> int)
6. 'a ~ 'a
7. (args 'a int) ~ (args bool 'b)
8. (args 'a int) ~ ((args bool) -> 'b)
9. 'a ~ (pair 'a int)
10. 'a ~ tau // arbitrary tauWhat does it mean to solve constraints?
Two questions: what’s substitution, and when is a constraint satisfied?
just formalize it. It’s a function that behaves a certain way.
Constraint satisfaction: equal types mean equal constructors applied to equal arguments—same is in eqType.
Check your understanding: Substitutions and satisfied constraints
Answer the following questions.
- The constraint τ1 ~ τ2 is satisfied if τ1 = τ2.
- True
- False
- A substitution θ is a mapping from type variables to type variables, but not more complex types.
- True
- False
- A substitution θ ``solves’’ a constraint C by ensuring all types related in C via the ~ equivalence relation are equal.
- True
- False
Solving simple type equalities
Reflection: Solving type-equality constraints
One type of constraint we need to solve is that involving two types τ1 ∼ τ2.
Recall that each type can have one of three forms:
datatype ty
= TYVAR of tyvar
| TYCON of name
| CONAPP of ty * ty listBriefly describe how you would determine whether the constraint τ1 ∼ τ2 was satsified.
How many potential cases are there to consider?
Solving conjunctions
Check your understanding: Solving constraints
- When asked to produce a substitution θ that solves an equality constraint, which has the form τ1 ~ τ2, there are nine cases to consider. The number nine comes from the fact that each type has three possible forms: a type variable α, a type constructor μ, or a type application (τ1,…,τn)τ.
- True
- False
- When asked to produce a substitution θ that solves an equality constraint, which has the form τ1 ~ τ2, if τ1 has the form μ1 and τ2 has the form μ2, then there is no solution.
- True
- False
- When asked to produce a substitution θ that solves an equality constraint, which has the form τ1 ~ τ2, if τ1 has the form μ1 and τ2 has the form (τ1,…,τn)τ then there is no solution.
- True
- False
- In the type system we have been studying, the constraint α ~ α * τ is solvable.
- True
- False
- When solving the conjunction of constraints C1 ∧ C2, it is sufficient to produce a solution θ1 for constraint C1 and a separate solution θ2 for constraint C2, and then compose those substitutions to produce a solution θ1 o θ2 for the conjunction C1 ∧ C2.
- True
- False
The inference algorithm, formally
4 November 2020: Instantiation and generalization
There are PDF slides for 11/5/2020.
Retrospective: Making type inference precise
Write one thing you learned about formalizing type inference so far and one question you have. Your answers may be anonymously shared with your classmates.
Reflection: Introducing type schemes
Suppose your type inferencer has produced a type that mentions a type variable α. Under what circumstances do you think it is safe to generalize that type to a polymorphic type scheme ∀ α . τ?
Introducing and eliminating type schemes
Moving from type scheme to types (Instantiation)
Moving from types to type scheme (Generalization)
Check your understanding: Instantiation
- Instantiation is the process of converting from a polymorphic type scheme σ to a monomorphic instance τ.
Such conversions always take place when variables are type checked using the Var typing rule.
- True
- False
- Consider the Var typing rule:
Suppose we want to infer a type for the expression
(if y (fst 2 3) 4)in the environment
Gamma = {fst : forall 'a 'b. 'a * 'b -> 'a, y : 'c}Suppose we instantiate fst as follows:
fst : 'c * 'b -> 'cThis instantiation and the expression gives rise to the following constraints:
'c ~ bool ;; because y:'c and y is tested by the if
'c ~ int ;; because first argument to fst is an intThese constraints aren’t satisfiable.
But, the expression should have the typing
'c ~ bool, Gamma |- (if y (fst 2 3) 4) : intWhat went wrong?
We ignored the freshness requirement when instantiating
fst.We ignored the distinctness requirement when instantiating
fst.Nothing: the program shouldn’t be typeable.
Bonus question: Why the distinctness requirement?
Consider again
Gamma = {fst : forall 'a 'b. 'a * 'b -> 'a, y : 'c}
??, Gamma |- (if y (fst 2 3) 4) : ??Now suppose we instantiate fst as follows:
fst : 'a * 'a -> 'a
Gamma |- fst 2 #tApplication rule yields constraints:
'a ~ int
'a ~ boolwhich aren’t satisfiable. Which means this code would also be erroneously flagged as an error.
Correct typing:
Gamma |- fst 2 #t : intThe mistake was ignoring the distinctness requirement when instantiating the type scheme.
From types to type scheme: Val rule
The set A above will be useful when some variables in τ are mentioned in the environment.
We can’t generalize over those variables.
Applying idea to the type inferred for the function fst:
generalize('a * 'b -> 'a, emptyset) =
forall 'a, 'b. 'a * 'b -> 'aNote the new judgement form above for type checking a declaration.
On the condition θΓ = Γ: Γ is “input”: it can’t be changed.
The condition ensures that θ doen’t conflict with Γ.
We can’t generalize over free type variables in Γ.
Their presence indicates they can be used somewhere else, and hence they aren’t free to be instantiated with any type.
Check your understanding: The full Val rule
Consider the Val rule:
In this series of questions, we will walk through using the Val rule to type check the following definition:
(val pick-t (lambda (y z) (pick #t y z)))in the context
Γ = { pick : ∀ α.bool $\cross$ α $\cross$ α $\arrow$ α}
- The first hypothesis above the line in the Val rule that we must check is the judgment C, Γ |- e : τ. Suppose we have already derived the following instance of that judgment as we infer a type for the right-hand side of the
pick-tdefinition:
$$ \begin{array}{l} \alpha_y \sim \alpha_p \land \alpha_z \sim \alpha_p, \Gamma \vdash \\ \quad \lit{(lambda (y z) (pick \#t y z)) }: \alpha_y \cross \alpha_z \arrow \alpha_p \\ \end{array} $$
To derive that judgment, which of the following might have been how the polymorphic
pickfunction was instantiated, assuming αy and αz are the types assumed for variablesyandz, respectively? Consider what instantiation would have been necessary to produce the observed constraints and resulting type.pick:bool$\cross$ αp $\cross$ αy $\arrow$ αypick:bool$\cross$ αz $\cross$ αz $\arrow$ αzpick:bool$\cross$ αp $\cross$ αp $\arrow$ αppick: αp $\cross$ αp $\cross$ αp $\arrow$ αp
- The next step is to produce a substitution θ that solves the constraints αy ~ αp ∧ αz ~ αp and leaves Γ unchanged (θ Γ = Γ). Which of the following substitutions is a such solution?
θ = { αz -> αp}
θ = { αy -> αp, αz -> αp}
θ = { αp -> αx, αz -> αp}
None of the above because they all change Γ.
- The next step is to generalize. Given the substitution θ = { αy -> αp, αz -> αp}, what type should be passed as the first argument to the
generalizefunction? (The second argument is the empty set because ftv(Γ) = ∅.
θ(αy $\cross$ αz $\arrow$ αp) = αp $\cross$ αp $\arrow$ αp
θ(αy $\cross$ αz $\arrow$ αp) = αz $\cross$ αz $\arrow$ αz
θ(α $\cross$ α $\arrow$ α) = α $\cross$ α $\arrow$ α
θ(αy) = αp
Reflection: Type inference for
letformConsider the following
nMLcode. ML will infer a type scheme for the first and third examples, but reports an error for the second.Say what each of the functions is attempting to do and explain why you think ML reports a type error for the second function.
(lambda (ys) (let ([s (lambda (x) (cons x '()))]) (pair (s 1) (s #t)))) <function> : (forall ['a] ('a -> (pair (list int) (list bool)))) (lambda (ys) (let ([extend (lambda (x) (cons x ys))]) (pair (extend 1) (extend #t)))) type error: cannot make int equal to bool (lambda (ys) ; OK (let ([extend (lambda (x) (cons x ys))]) (extend 1))) <function> : ((list int) -> (list int))Let with constraints, operationally:
typesof: returns τ1, …, τn and Cval theta = solve CC-prime from
map,conjoinConstraints,dom,inter,freetyvarsGammafreetyvarsGamma,union,freetyvarsConstraintMap anonymous lambda using
generalize, get all the σiExtend the typing environment Gamma (pairfoldr)
Recursive call to type checker, gets
C_b,\tauReturn
(tau, C' /\ C_b)
Check your understanding: The Let rule
The following questions ask about the Let rule:
The
let-bound variables x1, …, xn are given polymorphic type schemes within the scope of the body of thelete, but the type inferred for e is monomorphic.- True
- False
- If the constraint solver returned the substitution θ = {α -> (α, β)}, type inference would be able to proceed with calculating a residual constraint and generalization.
- True
- False
- The residual constraint C′ retains all information in the substitution θ that relates to any type variable that might be relevant after type checking the
letexpression as determined by being mentioned in the free type variables of the context Γ.
- True
- False
- During generalization, we only need to worry about not generalizing over the free type variables mentioned in Γ because those type variables might be constrained in various ways by other parts of the program.
- True
- False
Check your understanding: The val-rec and letrec rules
The key insight with the two recursive type inference rules is to follow a three-step process:
- Introduce a fresh type variable α to represent the unknown type for the recursive binding.
- Infer constraints and a type τ for the recursive binding as usual
- Add a constraint relating the type variable and the inferred type (α ~ τ).
Otherwise, the recursive variants of the type inference rules proceed just as the non-recursive versions.
- True
- False
Forall things
Managing Quantified types valandval-reclet,letrec, …lambdaFORALL contains all variables (because none are free in the context) FORALL contains variables not free in the context FORALL is empty Generalize over all variables (because none are free in the context) Generalize over variables not free in the context Never generalize 9 November 2020: Introduction to Object-orientation
There are PDF slides for 11/10/2020.
Retrospective: Type Inference
Write one thing you learned in the previous module about type inference and one question you have about that material.
Your responses may be anonymously shared with the rest of the class.
Reflection: Introduction to Object-Oriented Programming
Suppose you were implementing a drawing program that lets users manipulate various kinds of shapes: circles, triangles, diamonds, etc.
What information would each shape need to know to be able to respond to user commands to display itself or to move to a new location?
What information would each shape need to know about the other shapes?
What benefits would there be to minimizing the amount of information shared between objects?
How would you organize your code if you knew you were going to have to add lots of new shapes in the future?
Information Hiding
So far: Programming in the small
- Expressive power
Success stories:
- First-class functions
- Algebraic data types and pattern matching
- Polymorphic type systems
What about big programs?
- Immersion in pile of interpreter code: not fun
An area of agreement and a great divide:
INFORMATION HIDING (especially: mutable data) / \ / \ code reuse / \ modular reasoning / \ interoperability / \ internal access between reps / \ to reps / \ OBJECTS MODULES ABSTRACT TYPESKey idea: Interfaces
- Provide external abstraction of gory details
- Limit access so internals can evolve
Introduction to OOP
Example Languages: JavaScript, Ruby, Java, C++, Python, …
Goals:
- Abstraction
- Code reuse
- Scaling to large code bases
Mechanism:
- Every object is a black box
- All you can do is send it messages!
- What messages? What do they do?
That’s the protocol
(an example of an interface)
Object-oriented demo
Demo: circle, diamond, triangle cards with these methods:
Front:
Object 1 : Circlepos:cardinal-pointset-pos:to:cardinal-point coorddraw
Back:
Object 1: Circle;; stores center of shapecenter: coordmethods:...Message sends:
object1 set-pos:to: 'S (0,0)object1 pos: 'Nanswer:(0,2)object2 set-pos:to: 'S (0,2)object2 pos: 'Nanswer:(0,4)object3 set-pos:to: 'SW (0,4)object1 drawobject2 drawobject3 draw
Key concepts of object-orientation
Don’t ask about my form:
It’s not your concern!
(information hiding)Instead:
- Ask me to tell you something
- Ask me to do something
(In object-oriented world, imperative “do this” is common.)
If you ask me something, I might delegate to my parent.
(Code reuse: one parent can do things for many children.)
Functional vs. OOP mindset
Functional and procedural:
- I find out what form you are
- I decide what to do and how to do it.
- Function name comes first in the syntax.
Object oriented:
- I ask you what to do
- You decide how to do it, based on what form you are.
- Receiving object comes first in the syntax.
Reflected in the syntax: the decider comes first!
Examples
Print every element of a list
- Functional: Are you
nilorcons? - OOP: Ask every element to do something.
Multiplication of natural numbers, base 10
- Functional: Are you zero or nonzero?
- OOP: return a number that is 10 times yourself.
Check your understanding: Key concepts of object-orientation
In object-oriented programming, computation proceeds by sending messages to objects.
- True
- False
Information-hiding is important to large-scale programming because it allows a large program to be divided into smaller units that can be understood separately.
- True
- False
In both functional and object-oriented languages it is idiomatic to ask about the representation of arguments to functions/methods.
- True
- False
One way an interface supports programming-in-the-large is by limiting access to the internal details of part of a program so those details may evolve independently of the rest of the program.
- True
- False
the fact that the concepts are intertwined to the point that it is hard to present them one at a time. In this video, I’ll review some of the key terms to give you some context, but we’ll introduce them again as we see them in use.
Check your understanding: OOP Terminology
Match the OOP term to its definition:
OOP term:
- object
- class
- instance variables
- class method
- dynamic dispatch
- inheritance
- instantiation
Definition:
- construct used for defining objects
- imperative state allocated on a per-object basis
- process of creating an object from a class; the new object is called an instance of the class
- dynamic entity that receives messages
- behavior invoked at the class level typically for instantiating and initializing objects
- mechanism whereby one class can be defined by extending the behavior of a parent or super class
- another term for message sending
Check your understanding: Classes represent forms of data
When coding lists using object-oriented idioms, different classes are used to represent the different forms of data: one class for the empty list and another class for non-empty lists.
- True
- False
Basic OOP mechanism review
Message send replaces function application
(ns select: pred)vsfilter ns pred
- Receiver appears first: it’s in charge!
- Object responds to message by evaluating method
Method determined by object’s class
Not shown: a method can use primitive operations.
Check your understanding: Code selection via dynamic dispatch
Dynamic dispatch means it is the run-time class of the receiver object that determines the code to be executed.
- True
- False
Idiomatic object-oriented code often avoids conditionals through the use of dynamic dispatch, for example by sending messages to objects from different classes to trigger class-appropriate behavior instead of asking the object about its representation and then branching on the result.
- True
- False
The six questions for Smalltalk
Message passing
Look at
SEND- Message identified by name (messages are not values)
- Always sent to a receiver
- Optional arguments must match arity of message name
(no other static checking)
N.B.
BLOCKandLITERALare special objects.Check your understanding: The six questions for Smalltalk
In μSmalltalk, all values are objects, even booleans, integers, strings, classes.
- True
- False
Because μSmalltalk focuses so strongly on objects, it does not provide any language feature akin to anonymous functions.
- True
- False
The μSmalltalk type system statically guarantees that no message-not-understood errors will happen at run-time. That is, if a message
mis sent to an objectobjin the text of the program, thenobjbelongs to a class in which methodmis defined.- True
- False
10 November 2020: OOP Mechanisms
There are PDF slides for 11/11/2020.
Retrospective: Introduction to OOP
Write one thing you learned about OOP so far and one question you have. Your answers may be anonymously shared with your classmates.
Smalltalk syntax
little livecoding.
Coding in uSmalltalk
- ;; blocks
- (val twice [block (n) (n + n)])
- (twice value: 3)
- ;; note lightweight syntax for parameterless blocks
- (val delayed {(’hello println) 42})
- delayed
- (delayed value)
- ;; blocks sent to Booleans
- (val x 10)
- (val y 20)
- ;; Note the number of columns matches number of args
- ((x <= y) ifTrue:ifFalse: {x} {y})
- ;; numbers
- ;; Fractions: exact 1 / 3
- ;; (1/3) is a name; (1 / 3) is what you want!
- ((1 / 3) - (1 / 2))
- ((1 / 3) + 1) ;; mixing classes!
- ((1 / 3) asFloat) ;; software floating point
- (2 asFloat)
- ((2 asFloat) sqrt)
- (((2 asFloat) sqrt) squared)
- (100 squared)
- (it squared)
- … keep going until overflow …
- (use bignum.smt)
- 100
- (it squared)
- Try again, go until CPU cap, stack trace
Coding Interlude: Coding in Smalltalk
Consider the following code:
;; blocks (val twice [block (n) (n + n)]) (twice value: 3) ;; note lightweight syntax for parameterless blocks (val delayed {('hello println) 42}) delayed (delayed value) ;; blocks sent to Booleans (val x 10) (val y 20) ;; Note the number of columns matches number of args ((x <= y) ifTrue:ifFalse: {x} {y})Enter the code, run it, and observe the results.
Write a block
squarethat multiples its argument object by itself (the symbol*represents multiplication), and use it to square the number5.
Now answer the following questions:
- Why doesn’t entering
delayedcause the stringhelloto be printed and the number42to be returned? - Why does entering
(delayed value)cause the stringhelloto be printed and the number42to be returned? - What is the meaning of the braces, as in
{('hello println) 42} and in the arguments to theifTrue:ifFalse:method ({x}and{y}`)? - What about the syntax of the
ifTrue:ifFalsemethod tells you how many arguments it is expecting?
Classes
Check your understanding: Parts of a class definition
Consider the following class definition:
(class CoordPair [subclass-of Object] ;; Inherits from class Object [ivars x y] ;; Instance variables (class-method withX:y: (anX aY) ((self new) initializeX:andY: anX aY)) (method initializeX:andY: (anX aY) ;; private (set x anX) (set y aY) self) (method x () x) (method y () y) (method = (coordPair) ((x = (coordPair x)) & (y = (coordPair y)))) (method * (k) ;;;;;; Scaling and translation (CoordPair withX:y: (x * k) (y * k))) ... )Now answer the following questions.
- Class
CoordPairinherits from a classPair
- True
- False
- Objects instantiated from class
CoordPairhave four instance variables:x,y,anX, andanY.
- True
- False
- The class method
withX:y:is sent to the classCoordPair.
- True
- False
- The method
=is an instance method that is sent to objects instantiated from the classCoordPair.
- True
- False
- In the class
CoordPair, the identifierxis used as both an instance variable and an instance method.
- True
- False
coordPair; need to use accessor methods; common idiom.
Check your understanding: Access rights
Consider the following code:
(class CoordPair [subclass-of Object] ;; Inherits from class Object [ivars x y] ;; Instance variables (method initializeX:andY: (anX aY) ;; private (set x anX) (set y aY) self) (method x () x) (method y () y) (method = (coordPair) ((x = (coordPair x)) & (y = (coordPair y)))) ... )Now answer the following questions:
- In the class
CoordPair, the instance variableyis private, which means it is accessible within the methods of the class, but not elsewhere. As a result, it is accessible withininitializeX:andY:,y, and=. However, anyyinstance variable that might be part of the argument objectcoordPairis not accessible in the=method.
- True
- False
- μSmalltalk makes it impossible to access the method
initializeX:andY:outside of the classCoordPairbecause of the commentprivate.
- True
- False
invariants for each class in hierarchy.
Check your understanding: Object initialization
Consider the following code:
(class CoordPair [subclass-of Object] ;; Inherits from class Object [ivars x y] ;; Instance variables (class-method withX:y: (anX aY) ((self new) initializeX:andY: anX aY)) (method initializeX:andY: (anX aY) ;; private (set x anX) (set y aY) self) ... (method * (k) ;;;;;; Scaling and translation (CoordPair withX:y: (x * k) (y * k))) )Now answer the following questions:
- The method
*sends the messagewithX:y:to the classCoordPairto create a newCoordPairobject initialized with scaled upxandycoordinates.
- True
- False
- The class method
withX:y:sends thenewmessage toselfto allocate a freshCoordPairobject. It then sends the messageinitializeX:andY:to the resulting object to initialize its instance variablesxandyto the parameter valuesanXandaY.
- True
- False
- An alternative way to get a new
CoordPairobject in a method defined within theCoordPairclass would be to send the messageinitializeX:andY:toself.
- True
- False
Check your understanding: Special names self and super
- A method defined on an object
objsends a message to the special nameselfto invoke another one ofobj’s methods.
- True
- False
- A method defined in a class
Sthat inherits from classPsends a messagemto the special namesuperwhen it wants to use the method implementation thatPwould have used form.
- True
- False
the collction protocol:
definitions with more efficient implementations.
Check your understanding: Concrete and abstract classes
- An abstract class has exactly one abstract method whose implementation is
subclassResponsibility.
- True
- False
- The purpose of an abstract class is to define some concrete methods in terms of the abstract methods so that behavior can be inherited by subclasses.
- True
- False
Method Dispatch
dispatch. We’ll use Booleans as an example.
class implements: it’s interface. Often standard methods defined on all objects omitted (like print).
send a message to the object
true.Check your understanding: Method dispatch
- When a message is sent to an object, the runtime system searches for a corresponding method definition starting with the class that defined the object.
- True
- False
- If a message
mis sent to an objectobjand if the runtime system cannot find a method definition inobj’s class, then the system reports a message-not-understood error.
16 November 2020: OOP Case Study: The Number Hierarchy
There are PDF slides for 11/17/2020.
Case study: Magnitudes and numbers
Reflection: Design of a Number Hierarchy
Imagine you are designing a hierarchy of number types such as reals, floats, integers and fractions. How would you organize this hierarchy? How are these number types similar and how are they different?
Key problems on homework
Naturalis aMagnitude“Large integer” is a
Number
Check your understanding: Design of magnitude class
Consider the Magnitude Class
(class Magnitude ; abstract class [subclass-of Object] (method = (x) (self subclassResponsibility)) ; may not inherit = from Object (method < (x) (self subclassResponsibility)) (method > (y) (y < self)) (method <= (x) ((self > x) not)) (method >= (x) ((self < x) not)) (method min: (aMag) ((self < aMag) ifTrue:ifFalse: {self} {aMag})) (method max: (aMag) ((self > aMag) ifTrue:ifFalse: {self} {aMag})) )- What methods must a subclass of Magnitude implement at a minimum?
- <, =
- =
- <,>,=
- <,=,<=,>=,>
- True or False: Can you compare two instances of Magnitude for equality using the = method as defined?
- True
- False
receiver but represents the same value as the argument
Reflection: OOP Design: Implementing class Number
Code reuse is a powerful feature. Consider the methods negated, reciprocal, +, -, * / .
How might you implement some of these methods in terms of others?
Check your understanding: Design of number class
Consider the Extended Number Heirarchy
At a minimum what messages will instances of Fraction, Float and Integer be able to respond to?
- Methods defined in Number, Magnitude and Object
- Methods defined in Number only
At a minimum what messages will instances of Small Integer and LargeInteger be able to respond to?
- Only Methods defined in Number
- Methods defined in Number and Methods Defined in Integer
Fractions: A case study in information hiding and initialization
the denominator is always positive
If the numerator is zero, the denominator is 1.
The numerator and the denominator are reduced to lowest terms, that is, their only common divisor is 1.
Information revealed to others
Reflection: Implementing coerce
Coercion is the process of making an instance fit a specified type. For instance, the Integer 1 can be coerced to the Float 1.0.
Imagine you wanted to add a Float x to an Integer y without losing any precision. Which instance should be coerced to what type before adding?
The method coerce: implements this idea. It returns the value of the argument in the representation of the receiver. How would you implement coerce: ?
What does the caller of the method coerce: need to know about the type and protocol of the receiver?
Reflection: Implementing multiply on fractions
(class Fraction [subclass-of Number] [ivars num den] ;; invariants: lowest terms, minus sign on top ;; if num = 0, den = 1 ;; maintained by divReduce, signReduce (class-method num:den: (a b) ((self new) initNum:den: a b)) (method initNum:den: (a b) ; private (self setNum:den: a b) (self signReduce) (self divReduce)) (method setNum:den: (a b) (set num a) (set den b) self) ; private .. other methods of class Fraction ... )Consider implementing multiply between instances of the Fraction class. How do you multiply two fractions? How might you implement multiply given what we know about multiplying two fractions?
Controlled information sharing in an open system
Reflection: Implementing multiply across differnt kinds of numbers
How might you implement multiply when we have lots of different kinds of numbers with different representations?
In the following slide, the notation
:+and:-are value constructors for positive and negative large integers. Thenandmare magnitudes (natural numbers).Check your understanding: Double dispatch
What two things does a double dispatch method encode?
- Operation and protocol
- Operation and instance
- Instance and protocol
- Consider using double dispatch to implement multiplication between your objects.
For each item, consider your class, and then the class of the object you are being multiplied against.
Do you need to coerce yourself into a different type of number for the operation to be successful?
Choose the appropriate smalltalk code to accomplish what you’re asked to do.
- As small integer, you’re asked to multiply large positive integer N by self (aka timesLP: N)
- (self * n)
- ((self asLargeInteger) * N)
- As small integer, you’re asked to multiply small integer n by self (aka timesSP: n)
- (self * n)
- ((self asLargeInteger) * N)
- As large positive integer, you’re asked to multiply large positive integer N by self (aka timesLP: N)
- (self * n)
- ((self asLargeInteger) * N)
- As large positive integer, you’re asked to multiply small integer n by self (aka timesSP: n)
- (self * n)
- ((self asLargeInteger) * N)
- Take a look at the code below. Can you determine which class each method belongs to? Hint: Your instance knows it’s own type and broadcasts that to the object the method is operating on.
- (method + (aNumber) (aNumber addSmallIntegerTo: self))
- SmallInteger
- LargePositiveInteger
- (method * (anInteger) (anInteger multiplyByLargePositiveInteger: self))
- SmallInteger
- LargePositiveInteger
18 November 2020: Subtyping and Equality
There are PDF slides for 11/19/2020.
Retrospective: Double Dispatch
Write one thing you learned about Double Dispatch and one question you have. Your answers may be anonymously shared with your classmates.
Reflection: Subtyping
Consider when can an object of one type be used in a context expecting an object of another type.
What needs to be true for this substitution to work?
Hint: Imagine you need to pound a nail. In this context you expect to use a hammer. If you had to use something else besides a hammer, what needs to be true about the alternative object for to accomplish your task?
Subtyping
Check your understanding: Subtyping
- True or False: A subtype doesn’t need to understand all the messages of its supertype.
- True
- False
- True or False: If A is a subtype of B and B is a subtype of C A can understand all the messages of C.
- True
- False
Reflection: Subtyping vs. Inheritance
Subtyping describes the relationship between two objects in terms of what messages both objects understand.
Inheritance describes the relationship between two objects in terms of what code is shared between objects.
First, describe two objects that aren’t related via inheritance, but that are subtypes.
Next, describe two objects that are related via inheritance, but that aren’t subtypes.
Subtyping vs Inheritance
Check your understanding: Subtyping vs. Inheritance
- Match each term with the correct definition.
- Subtyping
- related in class definition
- substitutability
- Inheritance
-related in class definition- substitutability
- True or False: When you add a method to a class, you need to add it to all the classes which inherit from that class.
- True
- False
Reflection: Equality
When should two objects be considered equal? Consider comparing two strings with == in C. What problems could result?
Equality
Check your understanding: Equality
- True or False: Different types may require different notions of equality. For example a notion of equality between two integers may be different than a notion of equality between two functions, or two expressions or two strings.
- True
- False
Semantics of Equivalence
Check your understanding: Observational Equivalence
What is the key idea of Observational Equivalence?
Two values should be considered equal if no context can tell them apart.
Two values should be considered equal if they have the same structure or binary representation in memory.
Two values should be considered equal if there is a context which produces the same result for both.
Check your understanding: Equality in Smalltalk
Match each of the smalltalk operators ( =, == ) with the correct definition.
- ==
- Are two objects observationally equivalent?
- Are two objects pointing to the same place in memory?
- =
- Are two objects observationally equivalent?
- Are two objects pointing to the same place in memory?
Review: Designing with objects
Visibility rules
Private messages to self (or instance of self)
Secret protocol to other objects of the same class (which can be spoofed)
23 November 2020: Hiding information with abstract data types
There are PDF slides for 11/24/2020.
Retrospective: Object-oriented programming
Write one thing you learned about object-oriented programming and one question you still have. Your answers may be anonymously shared with your classmates.
Reflection: Introduction to Module Systems
Describe two issues that arise when working on large programs that to not arise when working on small ones.
Pick a particular language feature or programming idiom and describe why that feature or idiom makes programming-in-the-large either easier or harder.
Data abstraction
How to write large programs?
An area of agreement and a great divide:
INFORMATION HIDING (especially: mutable data) / \ / \ modular reasoning / \ code reuse / \ internal access / \ interoperability to rep / \ between reps / \ MODULES OBJECTS ABSTRACT TYPESIntroduction to Module Systems
Key idea: Internal details hidden behind clean interface
Implementation Interface ------------------ ----- | | | | | Module | | I | | | | | ------------------ ----- ^ ^ | | Nitty gritty - - Public faceKey idea: Hierarchical building blocks
------ ------ | C1 | | C2 | ------ ------ \ / \ / -------------------- | I3 | -------------------- | M3 | | ------ ------ | | | I1 | | I2 | | | ------ ------ | | | | | | | | | M1 | | M2 | | --------------------Terminology: a module is a client of the interfaces it depends on
Module system overview
Functions of a module system:
- Hide representations, implementations, private names
- “Firewall” separately compiled units
(promote independent compilation) - Possibly reuse units
Desirable features:
- Modular (i.e., independent) static type checking
- Separately compilable interfaces and implementations
Aside: C and C++ are cheap imitations
- C doesn’t provide namespaces
- C++ doesn’t provide modular type checking for templates
Interfaces
Collect declarations
- Unlike definition, provides partial information about a name
(usually environment and type)
Things typically declared:
Variables or constants (values, mutable or immutable)
example:val MAX_INT : intTypes example:
type natProcedures (if different from values)
example:val intOfNat : nat -> intExceptions
example:exception Negative
Key idea: a declared type can be abstract
Just like a primitive type
Cannot ask “how were you formed, and from what parts?”
Ways of thinking about interfaces
Specification or contract for a module
- The “type” of a module
- Includes contracts for all declared functions
Means of hiding information (“what secret does it protect?”)
A way to limit what we have to understand
- The unit of sharing and reuse
A contract between programmers
- Parties might be you and your future self
- Explainer of libraries
The best technology for structuring large systems.
- Estimated force multiplier x10
Check your understanding: Interfaces
- An interface can be thought of as the type of a module.
- True
- False
- An interface typically includes the implementation of one or more functions.
- True
- False
- An interface can declare a type but leave its definition abstract, forcing client code to treat that type abstractly, as if it were a primitive type.
- True
- False
Module Implementations
------ ------ | C1 | | C2 | ------ ------ \ / \ / -------------------- | I3 | -------------------- | M3 | | ------ ------ | | | I1 | | I2 | | | ------ ------ | | | | | | | | | M1 | | M2 | | --------------------Hold all dynamically executed code
- expressions/statements
May include private names
May depend only on interfaces, or on interfaces and implementations both
- max cognitive benefits when all dependency is mediated by interfaces
Dependencies may be implicit or explicit (
import,require,use)
Check your understanding: Modules and module systems
- A module provides the implementation of one or more interfaces.
- True
- False
- A module may have private information hidden from client code.
- True
- False
Standard ML Modules
The Perl of module languages?
Has all known features
Supports all known styles
Rejoice at the expressive power
Weep at
- the terminology,
- the redundancy,
- the confusing syntax
What we’ve been using so far is the core language
Modules are a separate language layered on top.
Signature basics
operation that quickly finds and removes a minimal element.
without knowing the details of the implementation.
Check your understanding: The anatomy of a signature
When specifying a value in an ML signature, it is necessary to give a type for that value.
- True
- False
An ML signature can specify types, but not type constructors.
- True
- False
An ML signature cannot include exceptions.
- True
- False
ML modules extended example: Numbers
Check your understanding: Number signatures
- Consider the
INTEGERsignature:
signature INTEGER = sig eqtype int (* <-- ABSTRACT type *) val ~ : int -> int val + : int * int -> int val - : int * int -> int val * : int * int -> int val div : int * int -> int val mod : int * int -> int val > : int * int -> bool val >= : int * int -> bool val < : int * int -> bool val <= : int * int -> bool val compare : int * int -> order val toString : int -> string val fromString : string -> int option endIn this signature, the representation of
intis kept abstract except for the fact that values of typeintmay be compared for equality using the built-in equality function.- True
- False
- Consider the
NATURALsignature:
signature NATURAL = sig type nat (* abstract, NOT 'eqtype' *) exception Negative exception BadDivisor val ofInt : int -> nat val /+/ : nat * nat -> nat val /-/ : nat * nat -> nat val /*/ : nat * nat -> nat val sdiv : nat * int -> { quotient : nat, remainder : int } val compare : nat * nat -> order val decimal : nat -> int list endGiven this signature, if you do not already have a value of type
nat, the only way to get a value one is to use theofIntfunction.- True
- False
Coding Interlude: Signature for a stack
Given the following SML structure, write a corresponding SML signature that hides the implementation as a list but allows polymorphic stacks to be created and elements to be pushed and popped.
Reflection: When does a structure match a signature?
If we can write structures and signatures independently, we must have some way to determine whether a given structure implements given signature.
Give examples of three different circumstances that would mean a given structure does not implement an interface. One such example would be that the interface requires the presence of a value
MAX_INTbut the structure fails to define such a value.Check your understanding: Signature ascription
- The principal signature of a structure is the signature that contains the maximal interface information for that structure.
- True
- False
- With opaque signature ascription (
Queue :> QUEUE), type information in the structure is hidden. Only information described in the ascribing signature is available to client code.
- True
- False
Abstract data types
Check your understanding: Module access to representations
Consider the signature
NATURAL:signature NATURAL = sig type nat (* abstract, NOT 'eqtype' *) ... val /+/ : nat * nat -> nat val /-/ : nat * nat -> nat val /*/ : nat * nat -> nat endNow answer the following question.
- In any structure implementing this signature, the code for the
/+/operation will be able to access the representation of both arguments.
- True
- False
30 November 2020: Functors and Extended Case Study
There are PDF slides for 12/1/2020.
Retrospective: Structures and Signatures
Write one thing you learned about structures and signatures so far and one question you have. Your answers may be anonymously shared with your classmates.
Reflection: Parameterizing a structure by another structure
We’ve seen a couple of different kinds of functions. A
lambdaexpression takes an expression-level value as an argument, while atype-lambdaexpression takes a type as an argument.
Suppose we introduced a new kind of function that took a structure as an argument and returned a structure as a result.How do you think we might we “type” the argument and the result?
What do you think such functions might be used for?
Functors (aka generic modules aka parameterized structures)
Check your understanding: Functors
- A functor is a function over structures that combines elements of higher-order functions and
type-lambda.
- True
- False
- Functor applications are evaluated at runtime.
- True
- False
Check your understanding: where type
Consider the following code:
signature ORDER = sig type t val compare : t * t -> order end signature MAP = sig type key type 'a table val insert : key -> 'a -> 'a table -> 'a table ... end functor RBTree(structure Ord : ORDER) :> MAP where type key = Ord.t = struct ... endNow answer the following questions.
- The
ORDERsignature defines an abstract typet.
- True
- False
- If applying the
RBTreefunctor to some concrete structureFoopasses the type checker, thenFoomust not define a typet.
- True
- False
- The
MAPsignature defines an abstract typekey.
- True
- False
- The structure that results from applying the functor
RBTreeto structureFoowill satisfy theMAPsignature refined by thewhere typeclause so thatkeytype is defined to be equal toFoo’s definition of typet.
- True
- False
Extended example: Error-tracking Interpreter
Why this example?
Sketch composing large systems
Lots of interfaces using ML signatures
Some ambitious, very abstract abstractions—it’s toward the end of term, and you should see something ambitious.
Practice implementing functors
Error modules: Three common implementations
Collect all errors
Keep just the first error
Keep the most severe error
Check your understanding: Error signature and implementations
Consider the
ERRORsignature:signature ERROR = sig type error (* a single error *) type summary (* summary of what errors occurred *) val nothing : summary (* no errors *) val <+> : summary * summary -> summary (* combine *) val oneError : error -> summary (* laws: nothing <+> s == s s <+> nothing == s s1 <+> (s2 <+> s3) == (s1 <+> s2) <+> s3 // associativity *) endNow answer the following questions.
- There is only one sensible way to implement this signature.
- True
- False
- In the signature, the type
errorrepresents one detected error.
- True
- False
- In the signature, the combinator
<+>concatenates a new error onto a summary of the errors detected so far.
- True
- False
Computations Abstraction
Ambitious! (will make your head hurt a bit)
Computations either:
return a value
produce an error
Errors must be threaded through everything :-(
Reflection: Error tracking interpreter
Given the
AllErrorsimplementation of theERRORsignature:structure AllErrors :> ERROR where type error = string and type summary = string list = struct type error = string type summary = error list val nothing = [] val <+> = op @ fun oneError e = [e] endand the following datatype declarations:
datatype 'a comp = OK of 'a | ERR of AllErrors.summary datatype exp = LIT of int | PLUS of exp * exp | DIV of exp * exp- Fill in evaluation code for
PLUScase using theAllErrorsimplementation ofERRORsignature:
fun eval (LIT n) = OK n | eval (PLUS (e1, e2)) = ...- Fill in evaluation code for
DIVcase using theAllErrorsimplementation ofERRORsignature:
fun eval (LIT n) = OK n | ... | eval (DIV (e1, e2)) - ...That’s really painful!
We can extend the computation abstraction with sequencing operations to help.
Example:
eval e1 + eval e2 (op +) (eval e1, eval e2) curry (op +) (eval e1) (eval e2) curry (op +) <$> eval e1 <*> eval e2The first three versions are not well typed. Why?
The last version will thread errors through the compuation behind the scenes.
Note:
eval e1, eval e2 : int comp curry (op +) : int -> (int -> int) <$> : (int -> (int -> int)) * (int comp) -> (int -> int) comp <*> : (int -> int) comp * int comp -> int comp curry (op +) <$> eval e1 : (int -> int) comp let pa = curry (op +) <$> eval e1 note by above, pa : (int -> int) comp pa <*> eval e2 : int compCheck your understanding: Computation combinators
Consider the signature of the computation abstraction:
signature COMPUTATION = sig type 'a comp (* Computation! When run, results in value of type 'a or error summary. *) (* A computation without errors always succeeds. *) val succeeds : 'a -> 'a comp (* Apply a pure function to a computation. *) val <$> : ('a -> 'b) * 'a comp -> 'b comp (* Application inside computations. *) val <*> : ('a -> 'b) comp * 'a comp -> 'b comp (* Computation followed by continuation. *) val >>= : 'a comp * ('a -> 'b comp) -> 'b comp endNow answer the following questions:
- The type
'a comprepresents a computation that either produces a value of type'aor results in an error.
- True
- False
- A value of type
'a compcreated by calling thesucceedscombinator will always return a value of type'a.
- True
- False
- The
<*>combinator applies a pure functionfwith type'a -> 'bto a value with type'a comp.
- True
- False
Check your understanding: Using the computation abstraction
Consider the following code for implementing an expression interpreter using the computation abstraction:
functor InterpFn( structure Error : ERROR structure Comp : COMPUTATION structure Env : COMPENV val zerodivide : Error.error val error : Error.error -> 'a Comp.comp sharing type Comp.comp = Env.comp) = struct val (<*>, <$>, >>=) = (Comp.<*>, Comp.<$>, Comp.>>=) datatype exp = LIT of int | VAR of string | PLUS of exp * exp | DIV of exp * exp fun eval (e, rho) = let fun ev(LIT n) = Comp.succeeds n | ev(VAR x) = Env.lookup (x, rho) | ev(PLUS (e1, e2)) = curry op + <$> ev e1 <*> ev e2 | ev(DIV (e1, e2)) = ev e1 >>= (fn n1 => ev e2 >>= (fn n2 => case n2 of 0 => error zerodivide | _ => Comp.succeeds (n1 div n2))) in ev e end endNow answer the following questions:
- The
InterpFnfunctor takes as a parameter a value declaration that represents a divide by zero error. This value is used in the evaluation of theDIVoperation.
- True
- False
- The evaluation of the
VARcase can never fail and so doesn’t need to be part of the computation abstraction.
- True
- False
- The evaluation of the
PLUSoperation uses the<$>and<*>combinators to thread errors through the computation.
- True
- False
- In the evaluation of
DIV,n1is bound to the result of evaluatinge1only in the case wheree1evaluates without error.
Ife1evaluates to an error, the rest of the computation is short-circuited and the error is returned directly.
- True
- False
ML Module summary
2 December 2020: Drive-by tour of lambda calculus
There are PDF slides for 12/3/2020.
Retrospective: SML’s Module System
Write one thing you learned about ML’s module system so far and one question you have. Your answers may be anonymously shared with your classmates.
Reflection: Models of computation
Think back to our formal models of impcore and μscheme. The simpler a formal model is, while still capturing the essence of what is being modelled, the better, because it allows us to focus on what matters most.
In programming languages, we generally want the langauge to be Turing complete. Practically speaking, that means it has to be able to express conditionals, natural numbers, and general recursion.
Describe how you would go about designing a minimal language that supported these features.
Why study lambda calculus?
A metalanguage for describing other languages, known to all educated PL people
Church-Turing Thesis: Any computable operator can be encoded in lambda calculus
Theoretical underpinnings for most programming languages (all in this class).
Test bench for new language features
The world’s simplest reasonable programming language
Syntax: Only three forms!
M ::= x | \x.M | M M'Everything is programming with functions
Everything is curried
Application associates to the left
Arguments are not evaluated before application
First example:
(\x.\y.x) M N --> (\y.M) N --> MCrucial:
- Argument N is never evaluated (could have an infinite loop)
- Substitution is “capture-avoiding”
Programming in Lambda Calculus
Absolute minimum of code forms:
- no
set,while,begin - but also no
ifand nodefine!
Assembly language of programming languages
Systematic approach to constructed data:
- Everything is continuation-passing style
Alert to the reading: Wikipedia is reasonably good on this topic
- EXCEPT for the way they encode lists, which is bogus (violates abstraction)
Coding Booleans and
ifexpressionsQ: Who remembers the boolean-formula solver?
Q: What classes of results could it produce?
Q: How were the results delivered?
Q: How shall we do Booleans?
A Boolean takes two continuations:
- one for true, one for false
Laws:
true s f = s false s f = fCode:
true = \x.\y.x false = \x.\y.yCoding the if expression, laws:
if true then T else E = T if false then T else E = ETherefore, code is:
if B then T else E = if-then-else B T E = \B.\T.\E.B T ECode:
true = \x.\y.x false = \x.\y.y if = \b.\t.\e.b t eCoding Interlude: Coding
notin lambda calculusGiven that we can code booleans in lambda calculus as
true = \x.\y.x false = \x.\y.y if = \b.\t.\e.b t eyour job is to write the
notfunction.As a first step, write the algebraic laws for
not. What are the forms of the input data? For each form, what should the output be?Now write the code for
not
You can try out your code in the
lamstepinterpreter on the homework cluster.Coding data structures
Coding pairs
To pair two values, how many alternatives are there?
(A: one, pair constructor)How many continuations?
(A: two, one for each element of the pair)What information does each expect?
(A: the two elements of the pair)What are the algebraic laws?
fst (pair x y) = x snd (pair x y) = yCode
pair,fst,snd
pseudo-code:pair x y k = k x y fst p = p (\x.\y.x) snd p = p (\x.\y.y)lambda calculus:
pair = \x.\y.\k.k x y fst = \p.p (\x.\y.x) snd = \p.p (\x.\y.y)Code
pair,fst,sndpair x y k = k x y fst p = p (\x.\y.x) snd p = p (\x.\y.y) pair = \x.\y.\k.k x y fst = \p.p (\x.\y.x) snd = \p.p (\x.\y.y)
Coding lists
List laws
null? nil = true null? (cons x xs) = false car (cons x xs) = x cdr (cons x xs) = xsHow many ways can lists be created? (A: two:
nilandcons)How many continuations?
(A: two, one for each,knandkc)What does each continuation expect?
nil: nothingcons:carandcdr
For each creator, what are its continuation laws?
cons y ys kn kc = kc y ys nil kn kc = kn car xs = xs error (\y.\ys.y) cdr xs = xs error (\y.\ys.ys) null? xs = xs true (\y.\ys.false)What are the definitions?
cons = \y.\ys.\kn.\kc.kc y ys nil = \kn.\kc.kn car = \xs.xs error (\y.\ys.y) cdr = \xs.xs error (\y.\ys.ys) null? = \xs.xs true (\y.\ys.false)What do those second continuations look like? (This is the source of Wikipedia’s terrible hack)
What are the definitions?
cons = \y.\ys.\kn.\kc.kc y ys nil = \kn.\kc.kn car = \xs.xs error (\y.\ys.y) cdr = \xs.xs error (\y.\ys.ys) null? = \xs.xs true (\y.\ys.false)
Check your understanding: Coding data structures in lambda calculus
- The encoding of a pair constructor in lambda calculus is as a function that takes the two elements
xandyof the pair and a continuationkthat says what to do with those elements.
- True
- False
- The function
\p.p (\x.y.x)encodes thesndprojection function on pairs in the lambda calculus.
- True
- False
- Lists are coded in lambda calculus as functions that take two continuations: one for what to do if the list is nil and one for what to do if the list is a cons cell. The nil continuation takes no arguments, while the cons case takes one argument: what to do for the head of the list.
- True
- False
- The function
\xs.xs true (\y.\ys.false)encodes thenull?function on lists in the lambda calculus.
- True
- False
Coding numbers: Church Numerals
Check your understanding: Church numerals
- The Church numeral encoding of the number 3 is
\f.\x.f(f(f(f x)))
- True
- False
- The function
\n.\f.\x.f(n f x)is the successor function on Church numerals
- True
- False
Taking stock:
- bools
- pairs
- lists
- numbers
Q: What’s missing from this picture?
A: Recursive functions.
Astonishing fact: We don’t need
letrecorval-rec.- We can encode recursion in the lambda calculus!
- Recursion + numbers makes the lambda calculus Turing complete.
Reflection: Encoding recursion
What value of
f
solves this equation:
f = λn.if n = 0 then 1 else n × f(n − 1)?Coding recursion
Check your understanding: Encoding recursion
Consider the recursively-defined
lengthfunction:length = \xs.null? xs 0 (+ 1 (length (cdr xs)))If we were to take the fixpoint of the following functions, which of them would produce the
lengthfunction?lg1 = \lf.\xs.null? xs 1 (+ 1 (lf (cdr xs)))lg2 = \lf.\xs.null? xs 0 (+ 0 (lf (cdr xs)))lg3 = \lf.\xs.null? xs 0 (+ 1 (lf (cdr xs)))lg4 = \lf.\xs.null? xs 0 (+ 0 (lf (car xs)))
Using fixed points
Enrichment Reflection.
For extra credit, for each of the following recursive equations, say whether there is a solution, (ie, a recursive function that makes the equation true). If there is a solution, say whether it is unique and what it is.
f1 = \n.\m.(eq? n m) n (plus n (f1 (succ n) m)); f2 = \n.f2 (isZero? n 100 (pred n)); f3 = \xs.xs nil (\z.\zs.cons 0 (f3 zs)); f4 = \xs.\ys.f4 ys xs;Summary
Lambda calculus is Turing Complete
- Conditionals (via continuations)
- Numbers (via Church encoding)
- Recursion (via Y combinator)
Essence of most programming languages
- All that we have studied
Evaluation proceeds by substituting arguments for formal variables (called beta reduction)
7 December 2020: Producing Software with Integrity: Motivations, Capabilities, and Impediments
There were no PDF slides on 12/8/2020.
Retrospective: Lambda calculus
Write one thing you learned about lambda calculus so far and one question you have. Your answers may be anonymously shared with your classmates.
Reflection: Security-critical software
Despite high-profile data breaches stemming from flaws in software and frequent demonstrations of the insecurity of security and safety critical systems at Black Hat, high-quality security-critical software seems to remain elusive. Why do you think that might be?
Misused buffers are a major security problem
Graph showing number of buffer overflow
- CVE: Common Vulnerability and Exposures Database (>67,000)
- CWE: Common Weaknesses Enumeration (CWE) (120 categories)
CVSS: Common Vulnerability Scoring System (CVSS)
- score 1-10, above a 7 is ‘severe’
severe vulnerability has these characteristics:
- network based attack
- complexity is low
- no privilege is required
- no user interaction is required
- no workaround exists
buffer overflow most common: > 12,000 identified CVEs, more often than not secure
Examples:
- Heartbleed: missing bounds check, exfiltration
- Microsoft Security Bulletin MS15-078: buffer underflow, remote code execution in all supported windows platforms
Check your understanding: Software bugs lead to exploits
- Given all the vulnerabilities listed in MITRE’s Common Vulnerability and Expostures Database, issues related to misusing buffers are a relatively minor problem.
- True
- False
- Buffer overflow/underflow attacks such as Heartbleed and the issue reported in MS security bulletin MS15-078 can result in exfiltrating information from a system without leaving any trace in log files and/or allow a remote attacker to take over control of a computer.
- True
- False
Consequences of poor cybersecurity
Consequences of poor cybersecurity: Ransomware
Consequences of poor cybersecurity: Physical damage
Consequences of poor cybersecurity: Changing the nature of warfare
Check your understanding: Consequences of poor cybersecurity
- Ransomware is a way hackers can monetize malware. It typical works when hackers break into a system and encypt files. They then demand payment to decrypt the files. Whether or not victims pay the ransom, recovery costs can be in the millions of US dollars.
- True
- False
- When breaking into automobiles and other cyber-physical systems, hackers have to be physically close to the system they are attacking.
- True
- False
- Although disguised as anonymous ransomware, subsequent analysis has revealed that NotPetya constituted a purely destructive attack launched by one sovereign nation (Russia) against another (Ukraine). It caused billions of U.S. dollars of damage, both within the Ukraine and worldwide.
- True
- False
- There is no known evidence of successful attacks on critical infrastructure such as power distribution systems.
- True
- False
Reflection: Techniques to build better software
What approaches do you think might be effective for building higher quality software?
We know how to build higher-quality software
Check your understanding: Proof of concept for building higher-quality software
- No C code was involved in the high-assurance code for the SMACCMcopter or Boeing’s Unmanned Little Bird.
- True
- False
- At the end of DARPA’s HACMS program, the red team was unable to disrupt the flight operations or communication channels of Boeing’s Unmanned Little Bird despite being given root access to one of the partitions on the helicopter.
- True
- False
Reflection: Impediments to applying known technology
Assuming we do in fact know how to build higher-quality software, why do you think we might be choosing not to use such capabilities?
The economics of cybersecurity: Misaligned incentives and market failures
The economics of cybersecurity: Misaligned incentives
Check your understanding: Misaligned incentives
- In retail banking in the 1990s, the UK had lower fraud rates than the US because consumers were held responsible.
- True
- False
- Critical infrastructure operators are making uninformed decisions when they connect their cyber-physical systems to the internet given the security risks that such linkages cause.
- True
- False
Market Failure: Information asymmetries
Check your understanding: Information asymmetries
- Information asymmetry is a market failure that plagues the software security market: customers can’t evaluate the security of software and so aren’t willing to pay a premium for software with better security. As a result, vendors are reluctant to invest in better security because they won’t be able to recoup the cost in a higher price for their product.
- True
- False
- Another example of information assymetry in the software security industry is that lack of information about cybersecurity incidents. Lacking such data means we cannot properly assess the size of the problem, making it difficult to gauge whether we are properly allocating defensive resources.
- True
- False
Where do we go from here? Possible policy interventions
Possible policy interventions: Information disclosure
Possible policy interventions: Cyber insurance
Possible policy interventions: Software product liability
Check your understanding: Possible policy interventions
- Mandatory disclosure of data breaches has increased the attention paid to data breaches, making cyberinsurance for data breaches the most mature segment of the cyberinsurance market.
- True
- False
- Only a handful of insurance companies offer cyber insurance because it is too hard to measure the risk.
- True
- False
- The software industry has successfully lobbied against software product liability on the grounds that it would stifle innovation.
- True
- False
Producing software with integrity
Software flaws enabled by obsolete language design enable remote code execution and information exfiltration.
Poor cybersecurity has significant negative consequences at many levels: financial losses, damage in the physical world, and threats to national security.
We know how to build software to much higher quality standards using a variety of techniques. HACMS highlighted some of these, but there are many others.
Misaligned incentives and market failures such as information asymmetry explain why we are not building better software even though we know how.
Policy interventions are necessary to align incentives and fix market failures. Possible policy interventions include requiring information disclosure, mandating cyber insurance, or introducing product liability for software.
A Prediction
Cybersecurity is changing the nature of international conflict.
We are going to take it a lot more seriously
Hopefully before something goes catastrophically wrong.
9 December 2020: Comp 105 Conclusion
There are PDF slides for 12/10/2020.
Retrospective: Producing Software with Integrity
Write one thing you learned about producing software with integrity so far and one question you have. Your answers may be anonymously shared with your classmates.
Comp105 in Review
Review the highlights of what we’ve learned this semester:
- topics
- languages
- projects
Worth reviewing because it’s easy to lose track
- you’ve learned a lot!
Briefly discuss where you might go from here
- languages
- courses
What have you learned?
Type systems
Type inference
Object-Oriented Programming
Module Systems
Lambda Calculus
Producing software with integrity
Programming experience
Where might you go from here?